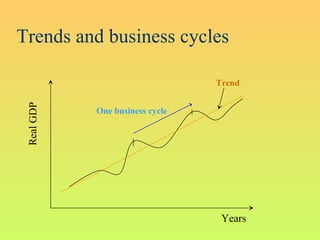
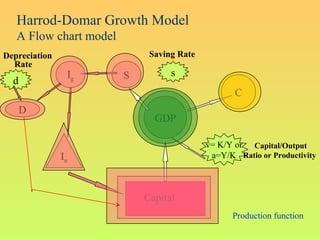
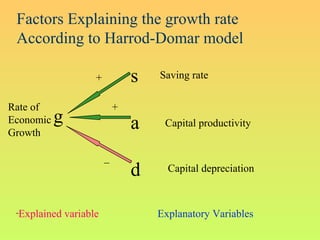
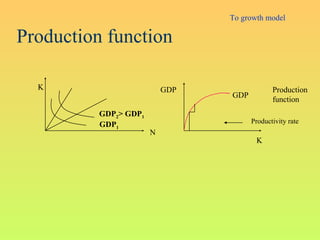
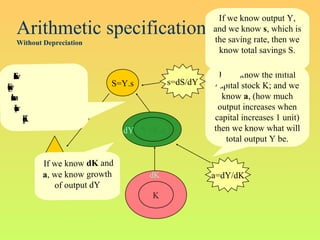
The Harrod-Domar growth model uses 3 key variables to determine the growth rate: 1. The saving rate, which determines how much can be invested. 2. Capital productivity, or how much output increases with each unit of new capital. 3. The depreciation rate, which accounts for aging of the existing capital stock. The model's formula is: Growth Rate = Saving Rate x Capital Productivity - Depreciation Rate. It provides a simple framework for analyzing how changes to these variables impact long-term economic growth.

1. Harrod-Domar Growth Model

2. Lord Harrod and Mr. Domar
Keynesian based models
Saving rates
Capital/Output ratio or
Capital Productivity
Capital stock
GDP
Personal Consumption
Gross Savings
Gross Investment
Net Investment, or Capital
Accumulation
Depreciation
Dynamic models
In growth models, we will encounter the
following terms:

3. What is a Keynesian Growth Model?
Keynes’ model and Keynesian models were
developed to explains business cycles
» A short run phenomena
As such they attribute a major role to aggregate
expenditures (demand side)
Regarding the supply side, they assume that there
is unemployment: production responds fast to
increases in aggregate demand because capital
and labor is unemployed.

4. Aggregate Demand, AD
– AD = C + I + G + X-M
– C, Consumption expenditures
– I, Investment expenditures
– G, Government expenditures
– X-M, Foreigners’ Expenditures
Aggregate Supply
– AS < ASfe
– Aggregate Supply, at full employment
Macroeconomic Equilibrium
– AS = AD
– Or
– S = I

5. A Keynesian Model
A Keynesian growth model takes a long run
perspective.
– Aggregate demand (or savings=investment)
still is important, but
– It also includes the aggregate supply
» Investment has two impacts:
On expenditures (in the short run)
On capital stock (in the long run)

6. Trends and business cyclesRealGDP
Years
One business cycle
Trend

7. Main Propositions
Economic growth can be accelerated by
– changing the saving rate
– improving technology.
Saving rates and technology can be
changed
– government interventions without
consideration to prices

8. v= K/Y or
a=Y/K
Capital
Capital/Output
Ratio or Productivity
GDP
s
Saving Rate
C
S
d
Depreciation
Rate
D
In
Ig
Production function
Harrod-Domar Growth Model
A Flow chart model

9. Factors Explaining the growth rate
According to Harrod-Domar model
g
s
a
d
Saving rate
Capital productivity
Capital depreciation
Rate of
Economic
Growth
Explained variable Explanatory Variables
+
+
_

10. Arithmetic specification
Without Depreciation
a=dY/dK
Y=K.a
S=Y.s s=dS/dY
I
K
dK
If we know the initial
capital stock K; and we
know a, (how much
output increases when
capital increases 1 unit)
then we know what will
total output Y be.
If we know output Y,
and we know s, which is
the saving rate, then we
know total savings S.
Ifweknowtotal
savingsS,weknow
howmuchwecan
invest(I)innew
capital(dK)
If we know dK and
a, we know growth
of output dY
dY

11. Numerical specification
Without Depreciation
a=.20
Y=1
S=.10 s=.10
.10
K=5
dK=.10
If we know the initial
capital stock K=5; and
we know its productivity
a=.20 then we know
total output Y=1
If we know output Y=1
and we know the saving
rate s=.10, then we know
total savings S=.10
Ifweknowtotal
savingsS=.10we
knowthatwecan
investI=.10innew
capital(dK=.10)
If we know dK=.10
and a=.20, we know
growth of output
dY=0.02=2%
dY=.02=2%
Or …
dY = s.a
By approximation:
dY/Y=s.a/Y
g=s.a
Since Y=1

12. Economic growth formula
According to Harrod-Domar the rate of economic growth
is defined by the formula:
g = s.a – d
that is, if s=10% and a=0.20 and d =1%, then
g=0.10*0.20 - 0.01 = 0.02 -0.01 = 0.01 = 1%
What happens if the rate of saving (s) increases to 20% ?
What happens if the productivity of capital (a) increases to 0.40?
What happens if the depreciation (d) rate is 2% ?

13. .
Conventional Keynes’ Model
Specification
Saving function (demand side)
S = s.Y where s is the average propensity to save or average saving
rate.
In the conventional short run Keynesian model investment (I) is given.
I = Ia
In equilibrium
S = I
Solving the model
s.Y = Ia
Y = 1/s.Ia = m.Ia where m is the investment multiplier
Mathematical derivation of Harrod-Domar model

14. In this model national GDP increases because the autonomous demand (I)
increases. It is assumed that aggregate supply responds as to produce
what is demanded. But, what will happen if the economy was at full
employment? The only way for production to increase will be an increase
in the capital stock. With more capital (and labor) the economy will
produce more GDP.

15. Mathematical derivation of Harrod-Domar model (2)
Keynes’ Model Expanded to Consider Growth
Harrod and Domar explained how the aggregate supply expands.
For them, investment has two effects, one on the aggregate demand
side (businesses expend more) and another in the aggregate supply
side (more investment increases capital stock and thereby
businesses produce more the next period).
We, therefore, need to add a production function:
Y = a.K production function
Where a is the productivity of capital: ∆Y/ ∆K, which is constant
Now we can determine how a change in capital changes income.
∆Y = a.∆K

16. Mathematical derivation of Harrod-Domar model (3)
What we need to know is how capital changes. It changes by
businesses, and government investment:
∆K = Ia
We are assuming that capital doesn’t ware out, i.e. there is not
depreciation.
Returning to the equilibrium condition (S=I) we solve the model again
for the long run case
s.Y = Ia = ∆K, but we know that ∆K = ∆Y/a, then
s.Y = ∆Y/a
s.a = ∆Y/Y
Calling ∆Y/Y = g : rate of GNP growth

17. Mathematical derivation of Harrod-Domar model IV
g = s.a
If we recognize that capital depreciates:
g = s.a – d
Where d is the depreciation rate per year.
Notice that in this model the rate of
growth (g) is constant. Why?

18. Harrod’s way:
K = v.Y where v = 1/a
g = s/v
And with depreciation
g = s/v - d

19. Production function
K
N
GDP1
GDP2> GDP1
Production
function
GDP
K
GDP
Productivity rate
To growth model

20. Assumptions
– Labor/capital proportions are fixed
– Saving rate is given
K
N
GDP1
GDP2> GDP1
S
S
Income = GDP
Production
function
Saving
function
GDP
K
GDP
Saving rate
Productivity rate
To growth model

21. Non-existence of equilibrium
K
Y,S,D,I Y
S
D
In
C
D

22. Review
Technology or
capital/output ratio
Saving rate
Depreciation rate
Capital accumulation
Growth rate
You should now be familiar with the following
terms: