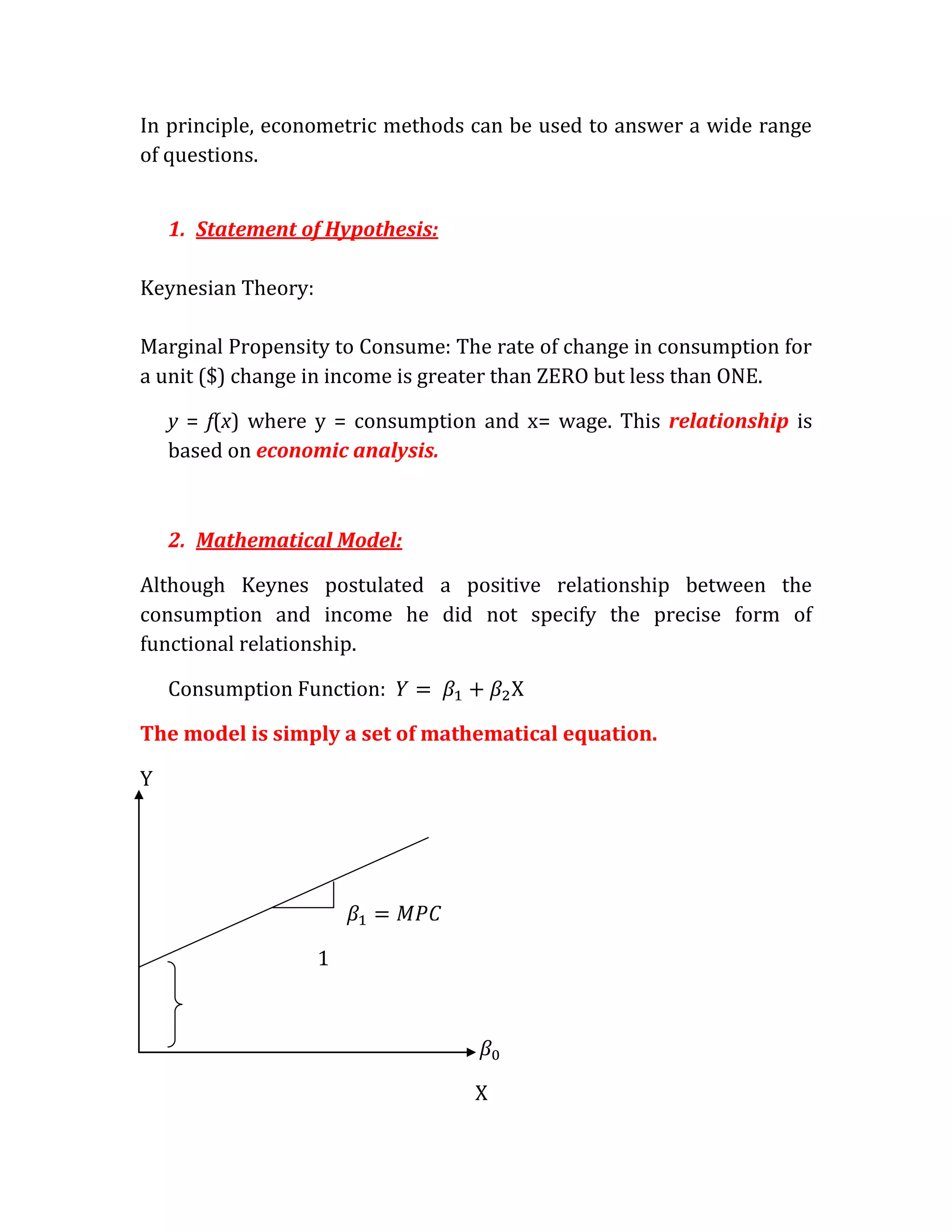
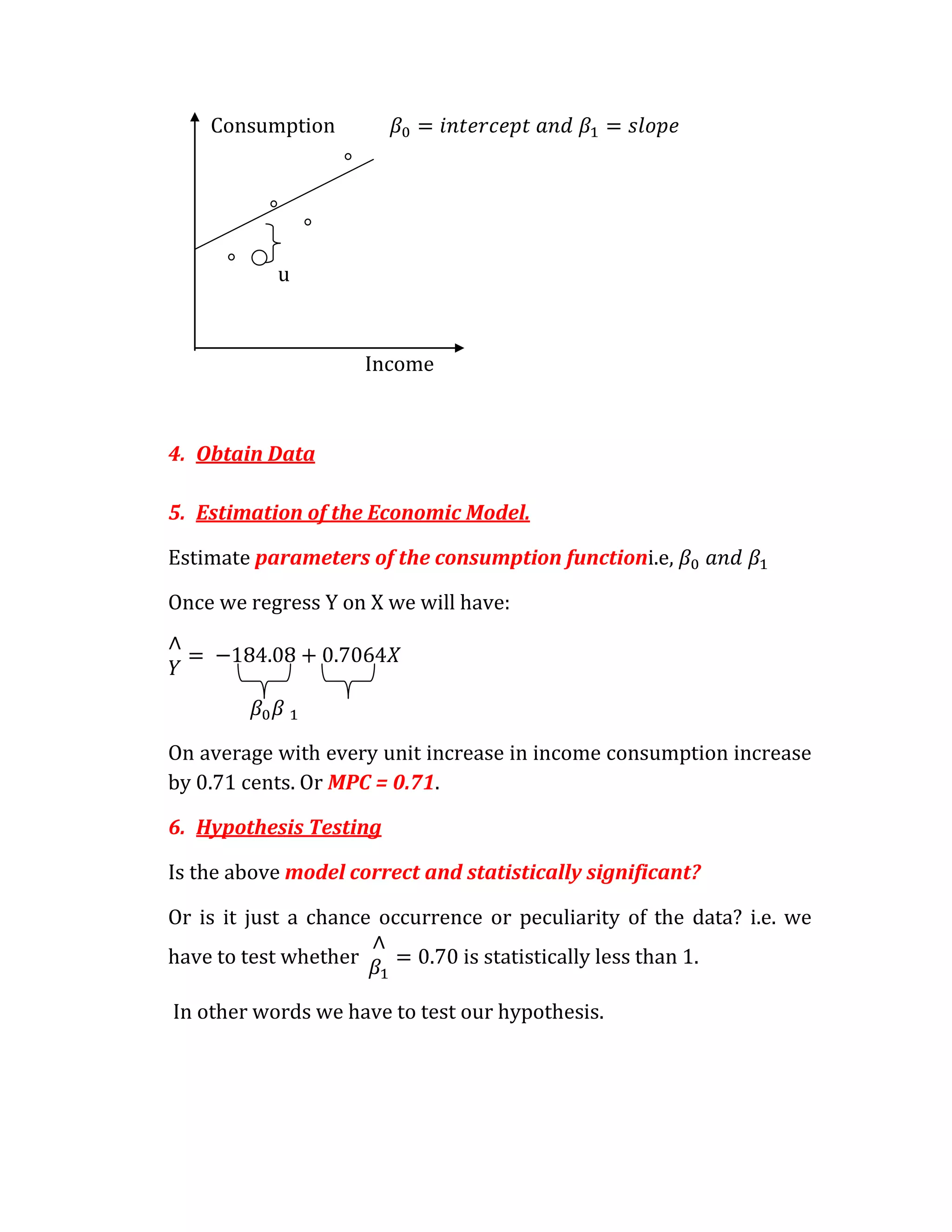
1. Econometrics uses statistical methods to estimate economic relationships, test economic theories, and evaluate policies. It builds mathematical and statistical models to represent economic behavior using data. 2. A consumption function model relates consumption (C) to income (Y) as C = a + bY, where a and b are parameters estimated using data. The model includes an error term to account for other influences not included. 3. Estimating the consumption function parameters using data allows testing hypotheses about marginal propensity to consume and forecasting future consumption based on the model. Government can also use such models for policymaking.

1. Introduction:
What is Econometrics?
Econometrics is based upon the development of statistical
methods for estimating economic relationships, testing
economic theories, and evaluating and implementing
government and business policy.
Economic Measurement i.e. measument of things such as
economic system, market etc.
Micro Economics-Other things remaining the same, a decrease in
price are expected to increase the quantity demanded.
But does not provide any numerical measure of the relationship
between the two.
Does not provide a numerical measure; tell us how much quantity goes
up or down.
Economic Statistical collects data (raw) on GNP, unemployment, interest
rate, and so on.
So the econometricians use these data’s and build models bases on
mathematics.
Econometric methods are relevant in virtually every branch of applied
economics.
They come into play either when we have an economic theory to test
or when we have a relationship in mind that has some importance for
business decisions or policy analysis.
An empirical analysis uses data to test a theory or to estimate a
relationship.
How does one go about structuring an empirical economic analysis?
The question might deal with testing a certain aspect of an economic
theory, or it might pertain to testing the effects of a government policy.

2. In principle, econometric methods can be used to answer a wide range
of questions.
1. Statement of Hypothesis:
Keynesian Theory:
Marginal Propensity to Consume: The rate of change in consumption for
a unit ($) change in income is greater than ZERO but less than ONE.
y = f(x) where y = consumption and x= wage. This relationship is
based on economic analysis.
2. Mathematical Model:
Although Keynes postulated a positive relationship between the
consumption and income he did not specify the precise form of
functional relationship.
Consumption Function: X
The model is simply a set of mathematical equation.
Y
1
X

3. Where
As X increase by one unit Y has to increase by less than one unit.
Linear in nature & positive relationship.
Single Equation Model.
Deterministic Model, since we deal with a relationship of a certain
type. EXACT
3. Econometric Model
Base on the Mathematical Model we build an economic model i.e.
Economic models are not exact. Samples.
+ +u
Where u; is the error or the disturbance term.
Income is the cause consumptions the effect.
But does consumption solely depend on the income?
Interest rates, inflation rates etc. And captures all the other terms,
which the income is not able to capture in determining consumption.
We can add other factors like interest rate, inflation and so on to the
model but we cannot eliminate the entirely.
Thus dealing with the error term or the disturbance term is the essence of
any econometric analysis

4. Consumption
u
Income
4. Obtain Data
5. Estimation of the Economic Model.
Estimate parameters of the consumption functioni.e,
Once we regress Y on X we will have:
On average with every unit increase in income consumption increase
by 0.71 cents. Or MPC = 0.71.
6. Hypothesis Testing
Is the above model correct and statistically significant?
Or is it just a chance occurrence or peculiarity of the data? i.e. we
have to test whether is statistically less than 1.
In other words we have to test our hypothesis.

5. Such conformation or rejection of economic theories on the basis on
sample evidence is based on a branch of statistical theory know as
statistical inference or hypothesis testing.
7. Forecasting and Prediction.
Once we know that our chosen model is accurate we can use this
model to forecast or predict future values.
8. Use of Model for Control and Policy.
Government often uses these models for policy-making purposes.
Eg. If the government believes that if consumption expenditure in
1992 is approximately 4900 billion will keep the unemployment rate
at 4.2% then using the above economic model it can control X
variable to generate the desired target variable.
4900 = -184.0779+0.7064X or X = 7194.
Types of Data:
Cross Sectional Data: Data on one or more variable collected at same
point in time.
However sometimes the data on all units do not correspond to
precisely the same time period, thus in pure cross sectional data we
ignore the minor time difference.
The most important feature of cross sectional data is that these
data’s have been collected via random sampling.Eg: obtaining
information on wage, education, experience and other characteristics
by randomly drawing 500 people from the working population, then
we have a random sample from the population of all working people.
Eg: We want to know the current obesity in Kathmandu; we draw
a sample of 1000 people randomly from the population and
measure their height and weight.

6. The fact that the ordering of the data does not matter for econometric
analysis is a key feature of cross-sectional data sets obtained from
random sampling.
Time Series Data: Data’s collected on a variable or variables on a
regular time intervalsi.e, daily, weekly, monthly or annually
Eg: Data on a stock price collected every day, monthly automobile
sales, GDP, money supply ect.
Key feature of Time series data unlike cross sectional data is the fact
that economic observations can rarely, if ever, be assumed to be
independent across time.
Most economic and other time series are related, often strongly
related, to their recent histories.
Many weekly, monthly, and quarterly economic time series display a
strong seasonal pattern, which can be an important factor in a time
series analysis.
For example, monthly data on housing starts differs across the
months simply due to changing weather conditions.
Pooled Cross Sections:
Some data sets have both cross-sectional and time series features.
For example, suppose that two cross-sectional household surveys are
taken in the United States, one in 1985 and one in 1990.
In 1985, a random sample of households is surveyed for variables
such as income, savings, family size, and so on.
In 1990, a new random sample of households is taken using the same
survey questions. In order to increase our sample size, we can form
a pooled cross section by combining the two years.

7. Because random samples are taken in each year, it would be a fluke
if the same household appeared in the sample during both years.
Pooling cross sections from different years is often an effective way
of analyzing the effects of a new government policy.
The idea is to collect data from the years before and after a key policy
change.
Sources of Data:
Primary: Survey
Secondary: Internet, government and private agencies.
Causality and the notion of Cetris Paribus in Econometric Analysis:
For example, in analyzing consumer demand, we are interested in
knowing the effect of changing the price of a good on its quantity
demanded, while holding all other factors—such as income, prices of
other goods, and individual tastes—fixed.
If other factors are not held fixed, then we cannot know the causal
effect of a price change on quantity demanded.
The notion of ceteris paribus—which means “other (relevant) factors
being equal”—plays an important role in causal analysis.