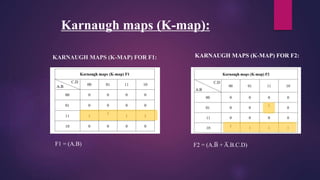
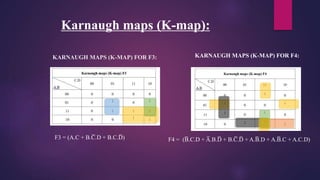
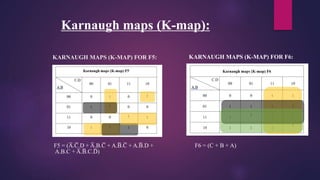
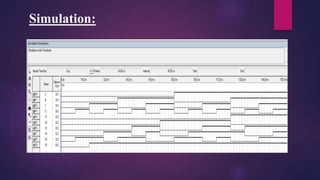
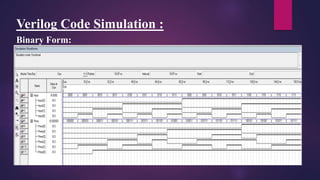
This document presents a mini project on designing a prime number generator circuit. It includes a problem statement, introduction, design process, logic design with a truth table and Karnaugh maps, circuit diagram, Verilog code simulation, analysis and conclusions. The design process generates up to 15 prime numbers using 4-bit input and 6-bit output. Karnaugh maps are used to simplify the Boolean expressions and derive the logic gate equations. The circuit and Verilog code are then simulated and the results analyzed. The presenters learned how to design digital logic circuits through this process.

2. PRESENTED TO:
Touhid Ahmed,
Lecturer,
Department of Computer Science and Engineering.
Course Title: Digital Logic Design
Course Code: CSE345
Section: 4
Semester: Spring 2021
Name ID
Md. Mizanur Rahman Riad Khan 2019-1-60-094
Md. Asad Chowdhury Dipu 2019-1-60-093
Asif Mahmud 2018-3-60-074
PRESENTED BY:

3. Mini Project Title:
Prime Number
Generator

4. Problem Statement:
Prime Numbers Generator.
4 bits input to 6 bits output.
Introduction:
Prime numbers is a common task in mathematics.
Prime numbers is also a common task in basic programming languages.
Prime numbers are important in the real world.

5. Design Process:
Design a logic circuit and simulate the circuit with Verilog HDL processes
are given below:
 Create a Truth Table for the Boolean expression of the logic gate.
 Simplifying Equation using Karnaugh maps (K-map).
 Verilog Code and Simulation.
 Circuit Drawing and Simulation.
 Analysis of the results.

6. Logic Design
: Truth Table:
A B C D F1 F2 F3 F4 F5 F6 Prime
Numbers
0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0 0 1 0 2
2 0 0 1 0 0 0 0 0 1 1 3
3 0 0 1 1 0 0 0 1 0 1 5
4 0 1 0 0 0 0 0 1 1 1 7
5 0 1 0 1 0 0 1 0 1 1 11
6 0 1 1 0 0 0 1 1 0 1 13
7 0 1 1 1 0 1 0 0 0 1 17
8 1 0 0 0 0 1 0 0 1 1 19
9 1 0 0 1 0 1 0 1 1 1 23
10 1 0 1 0 0 1 1 1 0 1 29
11 1 0 1 1 0 1 1 1 1 1 31
12 1 1 0 0 1 0 0 1 0 1 37
13 1 1 0 1 1 0 1 0 0 1 41
14 1 1 1 0 1 0 1 0 1 1 43
15 1 1 1 1 1 0 1 1 1 1 47

7. Simplifying Equation:
 Karnaugh maps (K-map) are used to facilitate the simplification of
Boolean algebra functions.
 Used Sum of Product (SOP) form.

8. Karnaugh maps (K-map):
KARNAUGH MAPS (K-MAP) FOR F1: KARNAUGH MAPS (K-MAP) FOR F2:
F1 = (A.B) F2 = (A.B
̅ + A
̅ .B.C.D)

9. Karnaugh maps (K-map):
KARNAUGH MAPS (K-MAP) FOR F3: KARNAUGH MAPS (K-MAP) FOR F4:
F3 = (A.C + B.C
̅ .D + B.C.D
̅ ) F4 = (B
̅ .C.D + A
̅ .B.D
̅ + B.C
̅ .D
̅ + A.B
̅ .D + A.B
̅ .C + A.C.D)

10. Karnaugh maps (K-map):
KARNAUGH MAPS (K-MAP) FOR F5: KARNAUGH MAPS (K-MAP) FOR F6:
F5 = (A
̅ .C
̅ .D + A
̅ .B.C
̅ + A.B
̅ .C
̅ + A.B
̅ .D +
A.B.C + A
̅ .B
̅ .C.D
̅ )
F6 = (C + B + A)

11. K-map Simplification output
From the above Karnaugh maps (K-map) simplification, we got the output,
 F1 = (A.B)
 F2 = (A.B
̅ + A
̅ .B.C.D)
 F3 = (A.C + B.C
̅ .D + B.C.D
̅ )
 F4 = (B
̅ .C.D + A
̅ .B.D
̅ + B.C
̅ .D
̅ + A.B
̅ .D + A.B
̅ .C + A.C.D)
 F5 = (A
̅ .C
̅ .D + A
̅ .B.C
̅ + A.B
̅ .C
̅ + A.B
̅ .D + A.B.C + A
̅ .B
̅ .C.D
̅ )
 F6 = (C + B + A)

12. Circuit Diagram:

13. Simulation:

14. Verilog
Code:

15. Verilog Code Simulation :
Binary Form:

16. Verilog Code Simulation :
Decimal Form:

17. Analysis:
 Verilog Code:
 End time is 160 ns.
 Grid Size is 1 ns.
 Functional simulation mode.
 Circuit Diagram:
 Grid Size is 1 ns.
 Functional simulation mode.

18. Discussions:
 Could not be generated more than 15 prime numbers.
 Implement the circuit on the breadboard will be better to analyze the results.
Conclusion:
Learned:
 Create a Truth Table for a specific problem.
 Simplification Boolean algebra functions using Karnaugh maps (K-map).
 Design a circuit diagram.
 Proper way to use the Quartus Simulation software.
 Analyze the results of the logic circuit and Verilog Code.

19. Thank you
 Any Question!