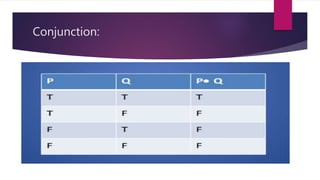
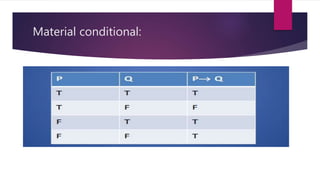
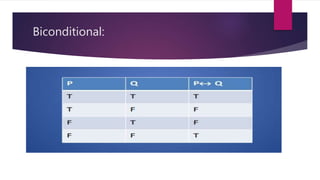
This document provides an overview of propositional logic, including its syntax, semantics, and inference rules. Propositional logic uses logical connectives and operators to connect or operate on propositions. The truth values of compound statements are determined by logical operators like negation, conjunction, disjunction, material conditional, and biconditional. Important inference rules of propositional logic are discussed, including modus ponens, simplification, conjunction, and transposition. Examples are given to illustrate how each rule can be used to validly derive conclusions.

1. Propositional Logic
BY:SURBHI SAROHA

2. SYLLABUS
 Syntax and semantics
 Review:Properties of statements
 Satisfiable
 Contradiction
 Valid
 Equivalence
 Logical consequences
 Inference Rules:Modus ponens,chain
rule,substitution,simplification,conjunction,transposition.

3. Syntax and semantics
 Syntax (the rules for how to take generate complex claims from simple ones)
 Semantics (the meanings of the atomic units, and rules governing how meanings of
atomic units are put together to form complex meanings)
 Syntax of PL
 Using logical connectives and operators (which connect or operate on propositions)
 Symbols: Use letters (P, Q, R, … X, Y, Z) to stand for specific statements Unary
propositional operator: ~ Binary propositional connectives: → , ↔ , • , ∨
 Grouping symbols: ( ), [ ]

4. Cont….
 Negation;
 not: ~ ~P
 Conjunction;
 and: • P•Q
 Disjunction; or: ∨ P∨Q
 Material conditional; if … then ..: → P→Q
 Biconditional: … if and only if …: ↔ P↔Q

5. Semantics of PL
 Semantic rules of PL tell us how the meaning of its constituent parts, and their mode of
combination, determine the meaning of a compound statement.
 Logical operators in PL determine what the truth-values of compound statements are
depending on the truth-values of the formulae in the compound.
 Logical operators defined by truth-tables.
 (T= true, F=false)
 Negation:
 P ~P
 T F
 F T

6. Conjunction:

7. Disjunction:

8. Material conditional:

9. Biconditional:

10. Propositional Logic
 The simplest, and most abstract logic we can study is called propositional logic.
 • Definition: A proposition is a statement that can be either true or false; it must be one
or the other, and it cannot be both.
 • EXAMPLES. The following are propositions:
 – the reactor is on;
 – the wing-flaps are up;
 – John Major is prime minister.
 whereas the following are not:
 – are you going out somewhere?
 – 2+3

11. Cont….
 The informal readings of some of the most standard connectives are as follows.
 • The conjunction denoted by ∧ is for and, as in “It is Monday and it rains”.
 • The disjunction denoted by ∨ is for or, as in “It is Monday or it is Tuesday”.
 • The negation denoted by ¬ is for not, as in “It is not the case that is is Monday”.
 • The implication denoted by → is for conditional truth, as in “If it is Monday then
it is not not week-end”.
 • The equivalence denoted by ↔ is for expressing that truth values are the same,
as in “It is week-end if and only if it is Saturday or Sunday.”

12. Inference Rules:Modus ponens,chain
rule,substitution,simplification,
conjunction,transposition
 Inference rules are the templates for generating valid arguments. Inference rules are applied to
derive proofs in artificial intelligence, and the proof is a sequence of the conclusion that leads to
the desired goal.
 In inference rules, the implication among all the connectives plays an important role. Following are
some terminologies related to inference rules:
 Implication: It is one of the logical connectives which can be represented as P → Q. It is a Boolean
expression.
 Converse: The converse of implication, which means the right-hand side proposition goes to the
left-hand side and vice-versa. It can be written as Q → P.
 Contrapositive: The negation of converse is termed as contrapositive, and it can be represented
as ¬ Q → ¬ P.
 Inverse: The negation of implication is called inverse. It can be represented as ¬ P → ¬ Q.

13. Types of Inference rules:
 1. Modus Ponens:
 The Modus Ponens rule is one of the most important rules of inference, and it
states that if P and P → Q is true, then we can infer that Q will be true. It can be
represented as:


14. Cont…..
 Example:
 Statement-1: "If I am sleepy then I go to bed" ==> P→ Q
Statement-2: "I am sleepy" ==> P
Conclusion: "I go to bed." ==> Q.
Hence, we can say that, if P→ Q is true and P is true then Q will be true.

15. Simplification:
 The simplification rule state that if P∧ Q is true, then Q or P will also be true. It can
be represented as:


16. Conjunction
 If P and Q are two premises, we can use Conjunction rule to derive P∧Q.
 PQ∴P∧Q
 Example
 Let P − “He studies very hard”
 Let Q − “He is the best boy in the class”
 Therefore − "He studies very hard and he is the best boy in the class"

17. Thank you