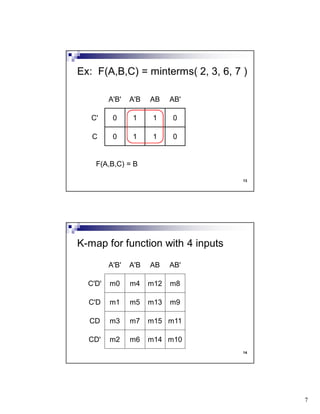
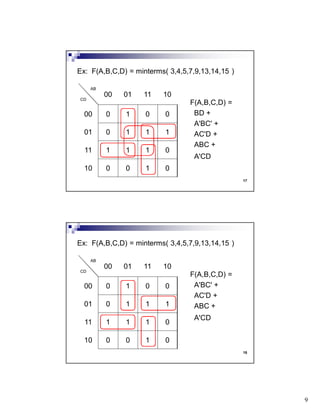
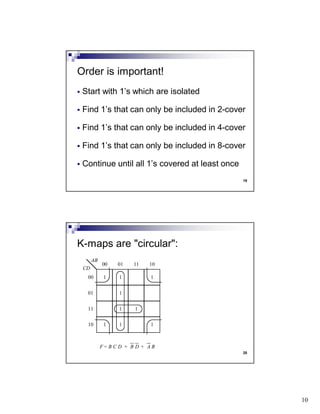
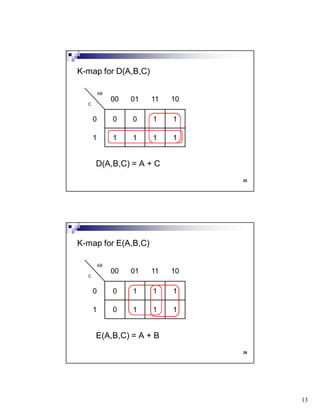
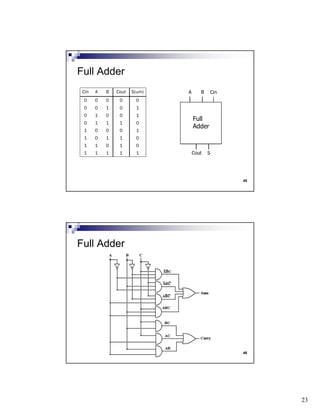
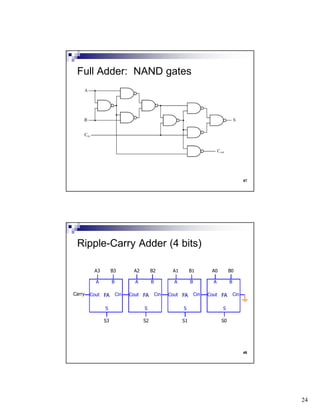
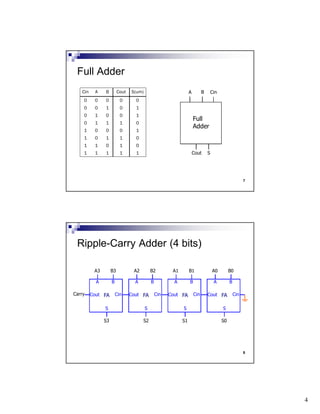
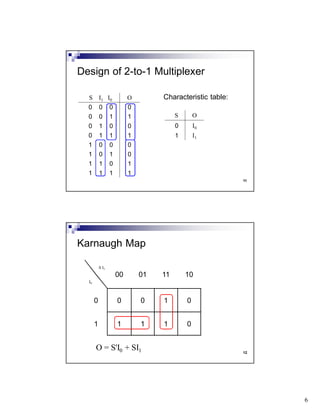
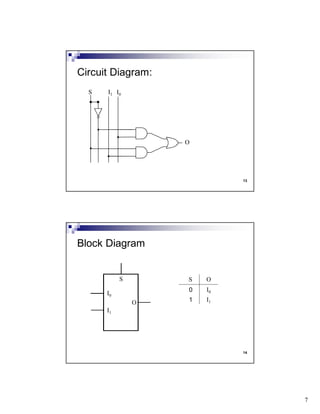
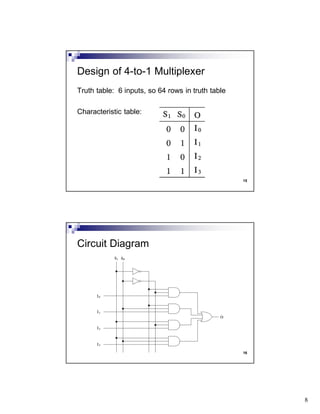
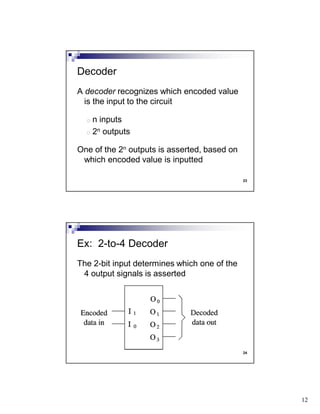
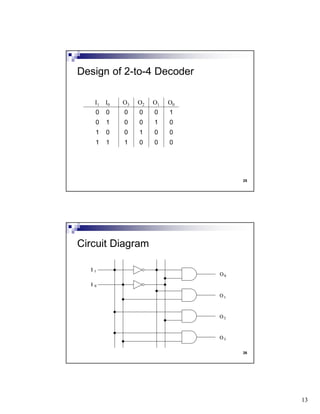
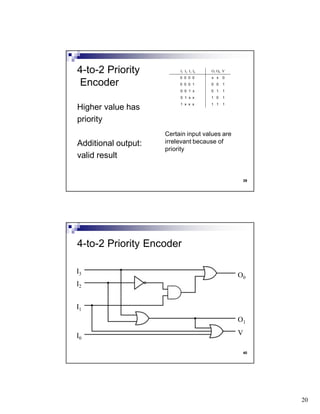
The document discusses combinational circuits and components. It covers topics like magnitude comparators, adders, multiplexers, and how they can be implemented using logic gates. Specifically, it provides examples of a 4-bit magnitude comparator and 4-bit ripple carry adder. It also discusses the design and truth table of a 2-to-1 multiplexer. Project 2 details are announced which involves designing eight logic functions.