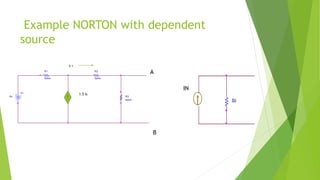
The document discusses Thevenin's and Norton's theorems. Thevenin's theorem states that any linear circuit can be reduced to an equivalent circuit with one voltage source in series with a single resistance. Norton's theorem states any linear circuit can be reduced to an equivalent circuit with one current source in parallel with a single resistance. The document provides examples of applying both theorems to complex circuits to find the equivalent Thevenin or Norton components. It also compares the two theorems noting Thevenin uses a voltage source in series with a resistance while Norton uses a current source in parallel with a resistance.

1. Thevenin and Norton
TheoremPresented by:
Gull Ahmed
M. Zaheer
Behzad
Muhammad Aqib Ali
Ahmed Hassan

2. Contents
 Thevenin Theorem
 Examples of Thevenin Theorem
 Norton Theorem
 Examples of Norton
 Comparison and difference of these theorems

3. Thevenin theorem
 Thevenin theorem was introduced by a French Telegraph Engineer
‘M Leon Thevenin’ in 1833.
 According to this theorem,
‘‘Any linear circuit consisting of several voltages and resistances can be
replaced by just on single voltage in series with a single resistance across
the load.’’
 Need of Thevenin
It is used to solve any complex circuits consisting of several dependent
and independent sources. We can solve any complex circuit by this
theorem

4. Implementation of Thevenin
 Conversion of complex circuit into Thevenin circuit.
R R
Vth
V I R
Rth
RL+
-
4 ohm
Rl
2 ohm
6 ohm6 ohm
+
_

5. Process
Following steps that are helpful for solving a complex circuit by Thevenin
theorem.
Step 1
 Remove the load resistor(RL) from the circuit.
 Replace load resistor with VTh.
 Make possible loops in the circuit.
 Then, fine current in the loops.
 We can find current by applying KCL theorem.
 This method helps us to find the Thevenin voltage.

6. Step 2
 Now we have to find Thevenin resistance.
 So, short all the voltages sources and calculate the equivalent resistance.
 This equivalent resistance is known as Thevenin resistance(Rth).
Rth = Req
Step 3
 After calculation of Thevenin resistance and Thevenin voltage we apply the
ohms law,
V = IR
 This gives us the current across the load resistor.

7. Thevenin Theorem
+
- 4 ohm
Rl
2 ohm
6 ohm6 ohm
Rth
RL+
-
2A
12v

8. Step 1
Rth= ?
RL remove …Vs short… Is open
 For Req
R = 6+6 = 12 ohm
Req = 1/12+1/4
= 3 ohm
Req = Rth = 3 Ω
4 ohm
6 ohm6 ohm

9. Step 2
Vth = ?
RL remove (open)..Voc =Vth
4 ohm
6 ohm6 ohm
+
_
12v 2A

10. Using Nodal Analysis
At node 1 Sub eq A from B
12-V1/6 + 2 = V1-V2/6
12-V1+12=V1-V2 2V1-V2= 24
2V1-V2= 24 2V1-5V2=O
At node 2 V1-V2/6=V2/4 4V2 = 24
4V1-4V2=6V2
2V1-5V2=O V2 = 6 volts (V)
A
B

11. Now using voltage divider rule
 For I load
I = Vth/Rth+RL
= 6/3+2
I= 1.2amp(A)
Rth
RL
+
-
6v

12. Norton theorem.
 Norton's theorem was independently derived in 1926 by engineer Edward
Lawry Norton (1898–1983).
 Norton theorem states” Any linear complex electrical
network with voltage and current sources and only resistances can be
replaced at terminals A–B by an equivalent current
source In in parallel connection with an equivalent resistance Rn.

13. Norton equivalent circuit.
 Use current divider rule to find load current.


14. Steps of Norton theorem
1. Finding load resistor.

15. 2. Finding Norton current.
 Short circuit the load resistor.
 Remember: The short circuit
will effectively remove all the
components in parallel with it.
 Use KCL to find currents.
 Find the current through short circuit wire.
 The current through short circuit wire is actually the Norton current.

16. 3. Finding Norton resistance.
 Take original circuit and remove
load resistance.
 Replace voltage sources with
wires.
 Replace current sources with
breaks.
 Find equivalent resistance of
modified resistance.
 This equivalent resistance across
the terminals where load resistance
was connected is the Norton resistance.

17. 4. Putting values in equivalent circuit.
 Put value of Norton current.
 Put value of Norton resistance.
 Find value of current through
load resistance using current
divider rule.

18. Dependent source.
 Again we need Norton current
and Norton resistance.
 Norton current can be found
by same process.
 For Norton resistance we apply
1 amp test current by removing
load resistance or b/t terminals.

19.  Use nodal analysis to find
nodal voltages.
 Norton resistance can be
found by formula Rn=Vo/Io.

20. Example Norton Circuit
20ohm
20ohm2.5ohm15ohm
15ohm
+
_+
_
a b
IN
A
B
Rn
30v
50v

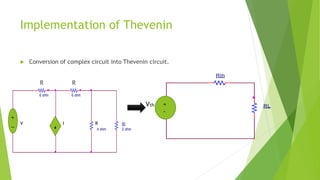
21. Step 1
remove the R(Load)
short the Vs
Open the Is
Rn=(15//15)+(20//20)
= [(15x15)/(15+15)]+[(20x20)/(20+20)]
= 7.5 + 10
Rn = 17.5Ω
20ohm
20ohm15ohm
15ohm

22. Step 2
short the RL  Applying Mesh Analysis
AT Mesh 1
-30+30I1-15I2=0
2I1-I2=2
AT Mesh 2
-15I1+35I2-20I3=0
-3I1+7I2-4I3
AT Mesh 3
40I3-20I2+50=0
4I3-2I2=-5
20ohm
20ohm15ohm
15ohm
50v
-
+
-
30v
+
I1 I2 I3
A
B
C
Note
I2=In

23. Solving the eq A,B and C
We get
I1=0.714A, I2=-0.571A, I3=-1.535A
AS I2=In ….
so I2=In= -0,571A
NORTON EQ.CIRCUIT
Rn
17.5 ohm
RL
2.5 ohm
Applying current divider rule
I = (In x Rn)/(Rn+RL)
= -0.571x17.5/17.5+2.5
I = -0.502A

24. Example NORTON with dependent
source
V1
6v
R2
3ohm
R3
4ohm
R1
5ohm
1.5 Is
V 1
A
B
IN
Rn

25. Step.1
 Short the load resistance
V1
6v
R2
3ohm
R1
5ohm
1.5 Is
Using nodal
analysis
(V1-6/5 )+Is=1.5 Is
(V1/5)/-(6/5)=Is/2
(V1/5)/-
(V1/6)=(6/5)
V1/30=6/5
V1=6x6
V1=36volts (V)
V 1

26. NOW Is=In
Is =In =V1/3 =36/3
In=12amp(A)
STEP.2
Rn=?
Short the voltage Source
Open the current Source
Dependent Sources Remain Same
Apply the test voltage(1V) or
current(1A)

27. Applying Nodal Analysis
AT Node 1 AT Node 2
3ohm5ohm
4ohm1.5Is 1A
V1 Vo
V1/5 – Is = 1.5Is
V1/5=Is/2
V1/5=V1-Vo/3x2
V1/5-V1/6=-Vo/6
V1/30=-Vo/6
V1=-5Vo
V1-Vo/3 –1=Vo/4
V1/3 -1 = Vo/4+Vo/3
(-5Vo/3)+1=7Vo/12
7Vo/12+5Vo/3=1
27Vo/12=1 Vo=4/9
Rn=V/I=(4/9)/1
Rn=4/9=0.44 ohm

28. Current divider rule
IN
Rn
Applying current divider rule
I = (In x Rn)/(Rn+RL)
= 12x0.44/0.44+2
I = 1.96 A

29. Compare Norton and Thevenin theorem.
Sr.No Parameter Thevenin
equivalent.
Norton’s
equivalent.
1. Components A voltage source
Voc and series
resistance Rth.
A Current source
Isc and shunt
resistance Rn.
2. Resistance Rth measured
between load
terminal by
shorting the Vs
and open Is.
Same.