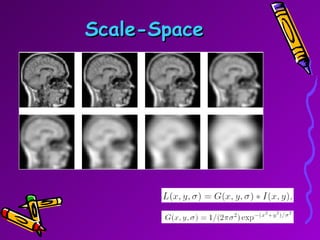
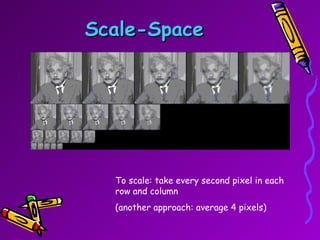
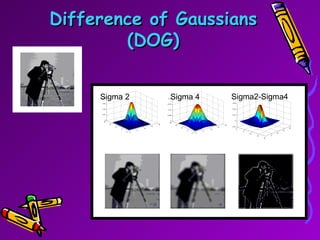
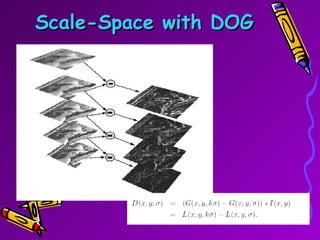
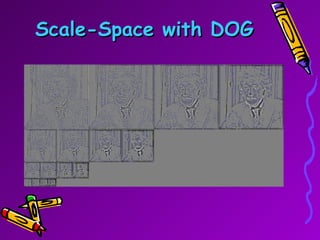
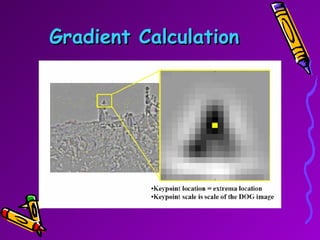
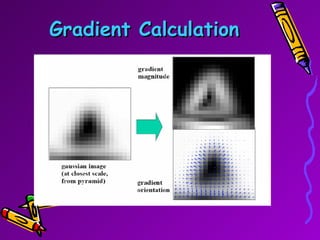
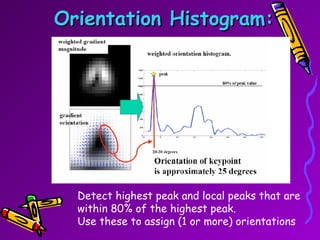
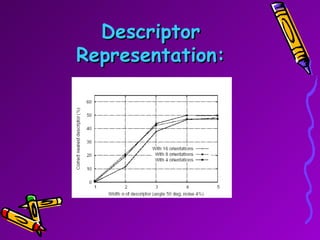
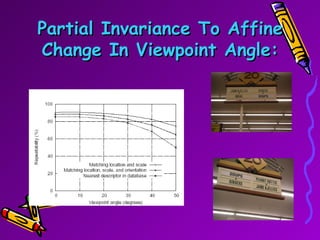
SIFT is a scale-invariant feature transform algorithm used to detect and describe local features in images. It detects keypoints that are invariant to scale, rotation, and partially invariant to illumination and viewpoint changes. The algorithm involves 4 main steps: (1) scale-space extrema detection, (2) keypoint localization, (3) orientation assignment, and (4) keypoint descriptor generation. SIFT descriptors provide a feature vector for each keypoint that is highly distinctive and partially invariant to remaining variations.