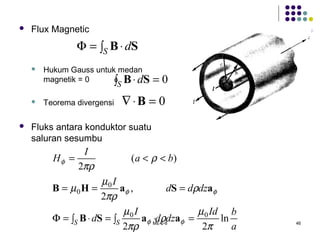
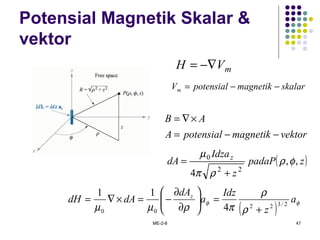
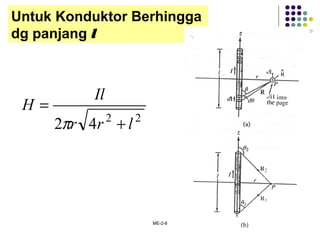
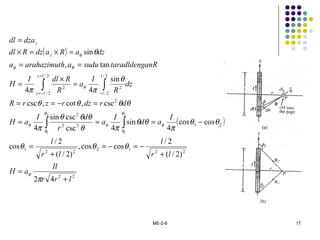
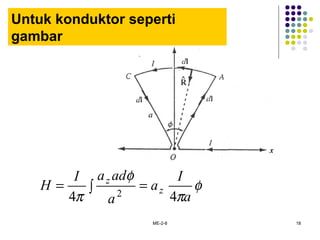
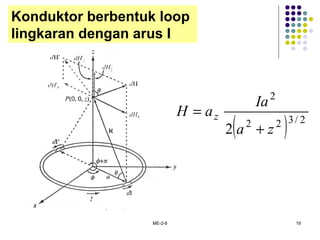
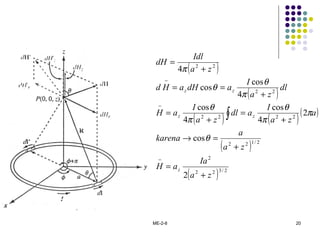
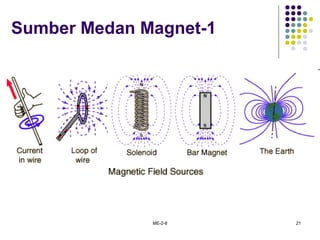
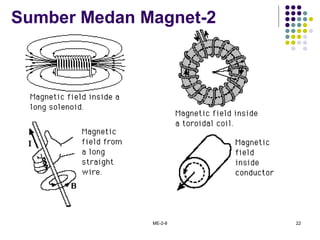
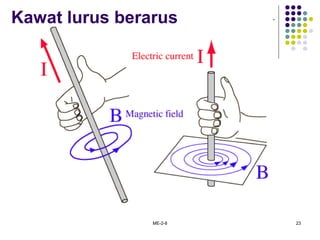
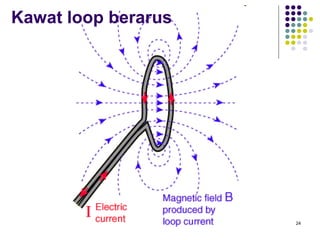
Dokumen tersebut membahas tentang medan elektromagnetik, yang mencakup: 1. Hukum Biot-Savart dan Ampere untuk menentukan intensitas medan magnet dari sumber arus. 2. Konsep kurl yang berhubungan dengan hukum Ampere. 3. Teorema Stokes untuk mengubah integral garis menjadi integral permukaan.

1. ME-2-8 1
Medan
Elektromagnetik
Achmad Mauludiyanto
Laboratorium Antena dan Propagasi
JTE ITS

2. ME-2-8 2
Pustaka
 Elektromagnetika Edisi 7 oleh William H.Hayt
dan John A.Buck, Penerbit Erlangga, 2006
 Fundamentals of Applied Electromagnetics
by Fawwaz T. Ulaby, Prentice Hall
International Inc., 2001
 Electomagnetics by Joseph A.Edminister,
Schaum’s ouline Series

3. ME-2-8 3
Materi
 8. Medan Magnet Konstan
 9. Gaya-gaya magnet, Bahan Magnetik, dan
Induktansi
 10. Medan Fungsi Waktu dan Persamaan-
persamaan Maxwell
 11. Gelombang Datar Serbasama

4. ME-2-8 4
8. Medan Magnet Konstan
1. Hukum Biot-Savart
2. Hukum Ampere
3. Kurl
4. Teorema Stokes
5. Fluks Magnetik dan
6. Kerapatan Fluks Magnetik
7. Potensial Magnetik Skalar & Vektor

5. ME-2-8 5
9. Gaya-gaya magnet, Bahan
Magnetik, dan Induktansi
1. Gaya pada sebuah muatan bergerak
2. Gaya pada sebuah elemen arus diferensial
3. Gaya antara elemen-elemen arus diferensial
4. Gaya dan Torsi pada sebuah rangkaian
tertutup
5. Sifat Dasar bahan magnetik
6. Magnetisasi dan Permeabilitas
7. Kondisi Bidang Perbatasan magnetik
8. Rangkaian Magnet
9. Indukatansi dan Induktansi silang

6. ME-2-8 6
10. Medan Fungsi Waktu dan
Persamaan-persamaan Maxwell
1. Hukum Faraday
2. Arus Perpindahan
3. Persaman Maxwell dalam bentuk titik
4. Persamaan Maxwell dalam bentuk
integral
5. Potensial tertinggal

7. ME-2-8 7
11. Gelombang Datar
Serbasama
1. Propagasi gelombang dalam ruang
hampa
2. Propagasi Gelombang dalam bahan
Dielektrik
3. Teorema Poynting dan Daya Gelombang
4. Propagasi di dalam bahan Konduktor
yang baik : efek kulit

8. ME-2-8 8
8. Medan
Magnet Konstan

9. ME-2-8 9
Pokok bahasan
 Hukum Biot-Savart
 Hukum Ampere
 Kurl
 Teorema Stokes
 Fluks Magnetik dan
 Kerapatan Fluks Magnetik
 Potensial Magnetik Skalar & Vektor

10. ME-2-8 10
Intensitas
medan magnetik
:
•Berbanding lurus dengan
perkalian arus (I), besar
panjang diferensial (dL)
dan sinus sudut antara
filamen dg garis yg
menghubungkan filamen
dg ttk P (sin θ)
•Berbanding terbalik dg
jarak kuadrat (r)
•Notasi : H satuan : (A/m)
∫
×
=
×
=
2
2
12
1211
2
4
4
R
Id
H
R
dI
d
R
R
π
π
aL
aL
H
Hukum Biot-Savart

11. ME-2-8 11
Kerapatan arus permukaan
∫=
s
R
R
dSKxa
H 2
4π
JdvKdsIdL ==

12. ME-2-8 12
φ
φ
φρ
ρ
ρ
ρ
πρρρπ
ρ
ρ
ρ
π
ρπ
ρ
ρπ
ρ
ρ
ρ
ρ
a
a
aaaa
H
aaa
H
aa
a
aaR
24
4
4
)(
4
)(
,
,
222
3
22
3
22
3
22
22
I
z
zI
z
dzI
z
zIdz
z
zIdz
d
z
z
z
zz
zz
z
R
z
=
+
=
∫
+
=∫
+
−×
=⇒
+
−×
=
+
−
=
−=
∞
∞−
∞
∞−
∞
∞−
Contoh
sebuah konduktor filamen dengan panjang tak berhingga yang membawa sebuah arus
searah I

13. ME-2-8 13
Garis-garis gaya dari
intensitas medan
magnet di sekitar
sebuah filamen lurus
tak berhingga yang
membawa arus
searah I, arah I
menembus masuk ke
dalam halaman ini.
φ
πρ
a
I
H
2
=

14. ME-2-8 14
( ) φαα
πρ
a
I
H 12 sinsin
4
−=
•Untuk konduktor berhingga
Intensitas medan magnet yang ditimbulkan
oleh sebatang filamen berarus dengan
panjang berhingga di sumbu-z

15. ME-2-8 15
Tentukan H di P2(0,4;0,3;0)
( )
( )
( ) ( )
( )
( )
( )( )
mAaaHHH
mAaaH
mAaaaH
zzyx
zzy
yy
x
xx
/37,6
20
/
8
9,36sin1
4,04
8
90;9,364,0/3,0tan
/
12
8,1
3,0
2
11,53sin
3,04
8
1,533,0/4,0tan,90
)(2)(22
0
)(2
0
2
01
1
0
)(2
01
2
0
1
−=−=+=
−
=−+=
=−=−=
==+=
==−=
−
−
π
ππ
αα
π
φ
ππ
αα
φφ

16. ME-2-8 16
Untuk Konduktor Berhingga
dg panjang l
22
42 lrr
Il
H
+
=
π

17. ME-2-8 17
( )
( )
22
22
12
22
1
2122
2
2
2/
2/
2
2/
2/
2
42
)2/(
2/
coscos,
)2/(
2/
cos
coscos
4
sin
4csc
cscsin
4
csc,cot,csc
sin
44
tan,
sin
2
1
2
1
lrr
Il
aH
lr
l
lr
l
I
ad
I
a
r
dI
aH
drdzrzrR
dz
R
I
a
R
RdlI
H
anRtaradldengsuduaharahazimuta
dzaRadzRdl
dzadl
l
l
lz
lz
z
z
+
=
+
−=−=
+
=
−===
=−==
=
×
=
==
=×=×
=
∫∫
∫∫ −
=
−=
π
θθθ
θθ
π
θθ
πθ
θθθ
π
θθθθ
θ
ππ
θ
φ
θ
θ
φφ
θ
θ
φ
φ
θφ
φ

18. ME-2-8 18
Untuk konduktor seperti
gambar
φ
π
φ
π a
I
a
a
adaI
H z
z
44 2
=∫=

19. ME-2-8 19
( ) 2/322
2
2 za
Ia
aH z
+
=
Konduktor berbentuk loop
lingkaran dengan arus I

20. ME-2-8 20
( )
( )
( ) ( )( )
( )
( ) 2/322
2
2/122
2222
22
22
2
cos
2
4
cos
4
cos
4
cos
cos
4
za
Ia
aH
za
a
karena
a
za
I
adl
za
I
aH
dl
za
I
adHaHd
za
Idl
dH
z
zz
zz
+
=
+
=→
+
=
+
=
+
==
+
=
−
−
−
∫
θ
π
π
θ
π
θ
π
θ
θ
π

21. ME-2-8 21
Sumber Medan Magnet-1

22. ME-2-8 22
Sumber Medan Magnet-2

23. ME-2-8 23
Kawat lurus berarus

24. ME-2-8 24
Kawat loop berarus

25. ME-2-8 25
Solenoida

26. ME-2-8 26
Solenoida & Magnet batang

27. ME-2-8 27
Solenoida

28. ME-2-8 28
Toroida

29. ME-2-8 29
Pokok bahasan
1. Hukum Biot-Savart
2. Hukum Ampere
3. Kurl
4. Teorema Stokes
5. Fluks Magnetik dan
6. Kerapatan Fluks Magnetik
7. Potensial Magnetik Skalar & Vektor

30. ME-2-8 30
 Menyatakan bahwa integral garis H untuk sebuah
lintasan tertutup persis sama dengan besarnya arus
searah yg dilingkari (diikat) oleh lintasan tersebut.
Id =∫ ⋅ LH
Hukum Rangkaian Ampere

31. ME-2-8 31
Contoh
 Lintasan yang dimaksud
harus berupa sebuah
lingkaran dengan jari-jari
ρ, sehingga hukum
rangkaian ampere
memberikan :
πρ
πρφρ
φ
φ
π
φ
2
22
0
I
H
IHdHdLH
=⇒
==∫ ∫=⋅
ρ

32. ME-2-8 32
•Konduktor sesumbu-1
( )
( )cb
bc
cI
H
cH
a
a
I
H
ba
I
H
<<
−
−
=
>=
<=
<<=
ρ
ρ
πρ
ρ
ρ
π
ρ
ρ
πρ
φ
φ
φ
φ
,
2
)(,0
)(,
2
,
2
22
22
2

33. ME-2-8 33
Besar intensitas medan sbg
fungsi jejari

34. ME-2-8 34
Arus permukaan
NKxaH
2
1
=
Sebuah lembaran arus
permukaan seragam
K=Kyay pada bidang
datar z = 0. H dapat
ditentukan dengan
Hk.Rangkaian Ampere
13
23
''
21
21
''
:32233
)(
:12211
xx
yxx
yxx
yxx
HH
KHH
jalur
KHH
LKLHLH
jalur
=
=−
−−−−
=−
=−+
−−−−
)0(
2
1
)0(
2
1
<−=
>=
zKH
zKH
yx
yx

35. ME-2-8 35
 Apabila sebuah konduktor kedua, dialiri arus
permukaan ke arah yang berlawanan K=-
Kyay , diletakkan di bidang z=h maka
),0(0
)0(
hzzH
hzaKH N
><=
<<×=

36. ME-2-8 36
Solenoida
a.Sebuah solenoida ideal
yang panjnagnya tak
berhingga dengan
sebuah lembaran arus
silinder-lingkaran
K=Kaaphi
b. Sebuah solenoide N-
lilitan dengan panjang
berhingga d.
zz
z
d
z
d
NI
d
NI
H
NIdHdzHdLH
aH =⇒=⇒
==∫ ∫=⋅ 0

37. ME-2-8 37
Toroida
degan N-
lilitan
Di bagian dalam toroida Di bagian luar toroida

38. ME-2-8 38
Curl-1
)(
)(11
silinderbentuka
HH
a
H
z
H
a
z
HH
r
xH z
zz
−





∂
∂
−
∂
∂
+





∂
∂
−
∂
∂
+





∂
∂
−
∂
∂
=∇
φρ
ρ
ρρφ
ρφ
φ
ρ
ρ
φ
)(cartesiana
y
H
x
H
a
x
H
z
H
a
z
H
y
H
xH z
xy
y
zx
x
yz






∂
∂
−
∂
∂
+





∂
∂
−
∂
∂
+





∂
∂
−
∂
∂
=∇
)(
)(1)(
sin
11)sin(
sin
1
bolabentuka
H
r
rH
r
a
r
rHH
r
a
HH
r
xH rr
r −





∂
∂
−
∂
∂
+





∂
∂
−
∂
∂
+





∂
∂
−
∂
∂
=∇ φ
θ
θ
φθφ
θφθφθ
θ
θ
NS
N
S
d
N ∆
∫ ⋅
=
→∆
LH
H
0
lim)(Curl

39. ME-2-8 39
Curl = Bentuk titik hukum integral Ampere
 Curl H = J atau ∇ x H = J
 Curl E = 0 0=×∇ E
Curl-2

40. ME-2-8 40
Pokok bahasan
1. Hukum Biot-Savart
2. Hukum Ampere
3. Kurl
4. Teorema Stokes
5. Fluks Magnetik
6. Kerapatan Fluks Magnetik
7. Potensial Magnetik Skalar & Vektor

41. ME-2-8 41
Teorema Stokes
SHLH dd S ⋅∫ ×∇∫ =⋅ )(
JH=×∇∫⋅=∫⋅×∇SSddSJSH)(Id∫=⋅LH

42. ME-2-8 42
contoh
 Gambar 8.16
 r=4, 0≤θ≤0,1π, 0≤φ≤0,3π
 Lintasan (1) : r=4, 0≤θ≤0,1π, φ=0
 Lintasan (2) : r=4, θ=0,1π, 0≤φ≤0,3π
 Lintasan (3) : r=4, 0≤θ≤0,1π, φ=0,3π
 Diketahui :
φφθφ ararH r cossin18sin6 +=

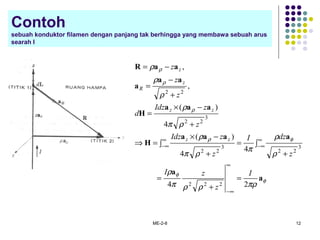
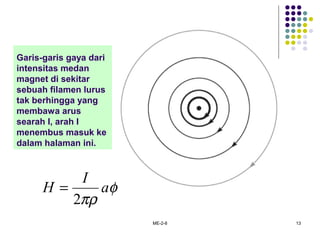
43. ME-2-8 43
Penyelesaian sebelah kiri
∫∫∫ ∫ ++=
321
sin. θφθθ θφθ rdHdrHrdHdLH
∫ ∫ ===
π
ππφπφπ
3,0
0
2
2,223,0sin1,0sin2881,0sin4]cos1,0sin)4(18[. AddLH
φθ φθθ adrarddradL r sin++=

44. ME-2-8 44
Penyelesaian sebelah kanan
θφθφ
θ
φθθ
θ
arr
r
a
r
H r 





−+=×∇ cossin36cos6
sin
11
)coscossin36(
sin
1
( )
Ad
dddSH
menjadiyaegra
addrdSkarena
s
r
2,223,0sin1,0sin288cossin
2
1
576
sin16coscos36).(
:lnint
sin
21,0
0
3,0
0
2
3,0
0
1,0
0
2
==





=
==×∇
−
=→
∫
∫ ∫ ∫
ππφφθ
φθθφθ
φθθ
π
π
π π

45. ME-2-8 45
Fluks Magnet
 Fluks yang menembus suatu luasan permukaan
 Satuan : Wb (weber)
 Kerapatan fluks magnetik (Magnetic Flux Density) : B
 Satuan : Wb/m2, T (tesla), G (gauss)
 1 Wb/m2 = 1 T = 10000 G
 Kerapatan fluks magnetik dlm ruang hampa
 Permeabilitas ruang hampa :
H/m104, 7
00
−
×== πµµ HB
0µ

46. ME-2-8 46
 Flux Magnetic
 Hukum Gauss untuk medan
magnetik = 0
 Teorema divergensi
 Fluks antara konduktor suatu
saluran sesumbu
∫ ⋅=Φ S dSB
0=∫ ⋅S dSB
0=⋅∇ B
a
bId
dzd
I
d
dzdd
I
ba
I
H
SS ln
22
,
2
)(
2
00
0
0
π
µ
ρ
πρ
µ
ρ
πρ
µ
µ
ρ
πρ
φφ
φφ
φ
=∫ ⋅=∫ ⋅=Φ
===
<<=
aaSB
aSaHB

47. ME-2-8 47
Potensial Magnetik Skalar &
vektor
mVH −∇=
vektormagnetikpotensialA
AB
−−=
×∇=
( )zpadaP
z
Idza
dA z
,,
4 22
0
φρ
ρπ
µ
+
=
skalarmagnetikpotensialVm −−=
( ) φφ
ρ
ρ
πρµµ
a
z
Idz
a
dA
dAdH z
2/322
00 4
11
+
=





∂
∂
−=×∇=

48. ME-2-8 48
Latihan-1
 Nyatakan nilai H dlm komponen kartesiuspd
P(0,01;0;0) di dlm medan :
1. Dua filamen arus 0,08A dlm arah az pd sb-z dan 0,08A
dlm arah –az pd x=0,015; y=0
2. Konduktor sesumbu a=3mm, b=9mm, c=12mm; I=0,8A
berpusat pd sb-z, arah az ditengah konduktor
3. Tiga lembar arus 1,5πay A/m di x=6mm, -3πay A/m di
x=9mm, dan 1,5πay A/m di x=12mm
4. Solenoida tak berhingga K= 3πaφ A/m di ρ=12mm
5. Toroida berpusat di ttk asal sumbu pd sb-y ρ0=12mm,
a=3mm, N=250lilitan, I=2mA dlm arah ay di jejari luar

49. ME-2-8 49
Latihan-2
1. Cari ∇xG
a. Dlm koordinat kartesius di ρA(3,2,1) jika
G=xyz(ax+ay)
b. Dlm koordinat tabung di ρB(2,300
,3) jika G= ρφzaz
c. Dlm koordinat bola di ρC(4,300
,450
) jika
G=sinθ(ar+aθ+aφ)
2. Sebuah konduktor padat tak bermagnet
berpenampang bundar mempunyai sumbu z dan dialiri
arus total 60 A yang terdistribusi serbasama dlm arah
az. Jika jejarinya 4mm, cari : (a) Bφ di ρ=5mm (b) Bφ di
ρ=3mm (c)fluks magnetik total persatuan panjang di
dlmkonduktor (d) c)fluks magnetik total persatuan
panjang di luar konduktor