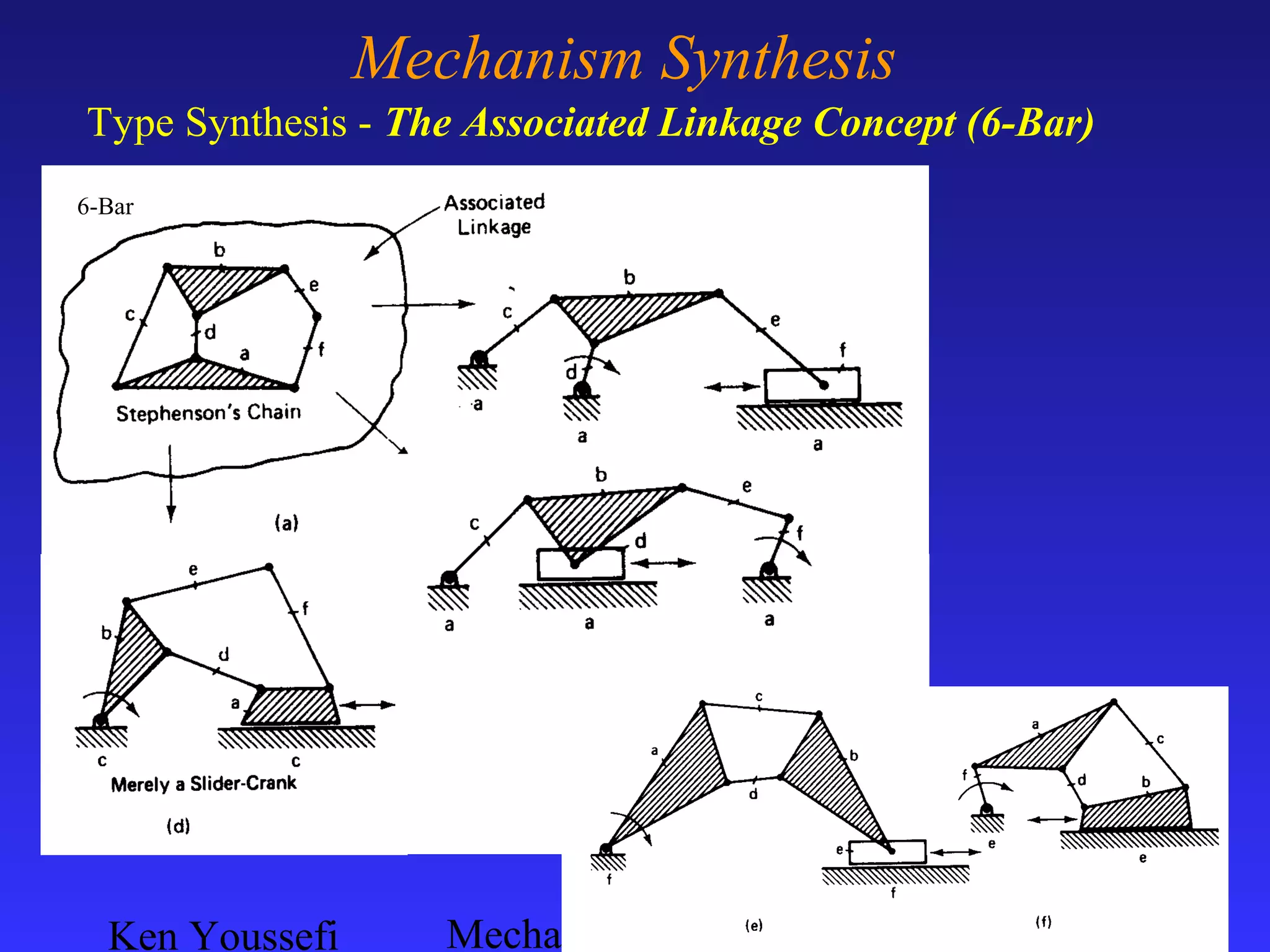
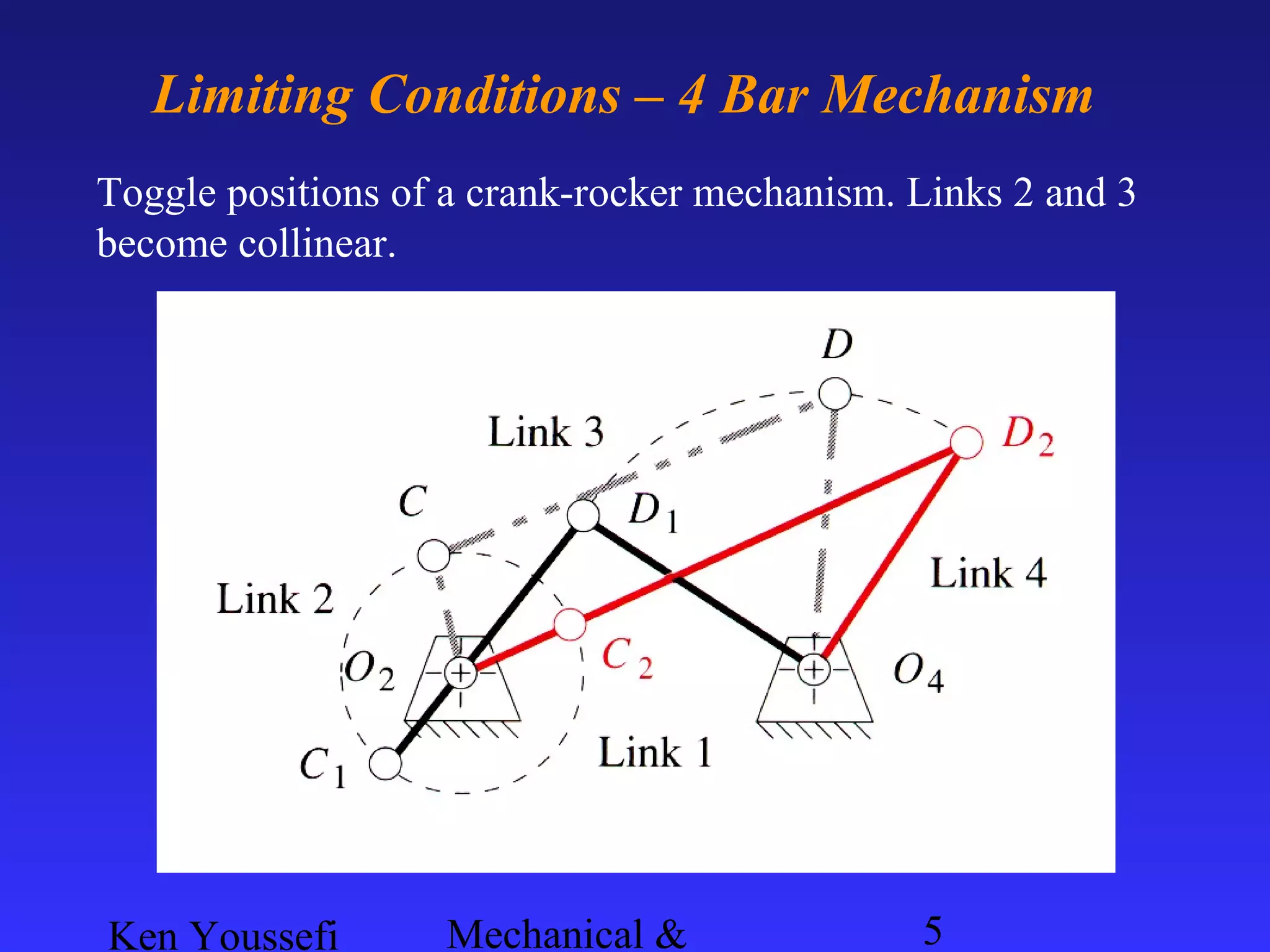
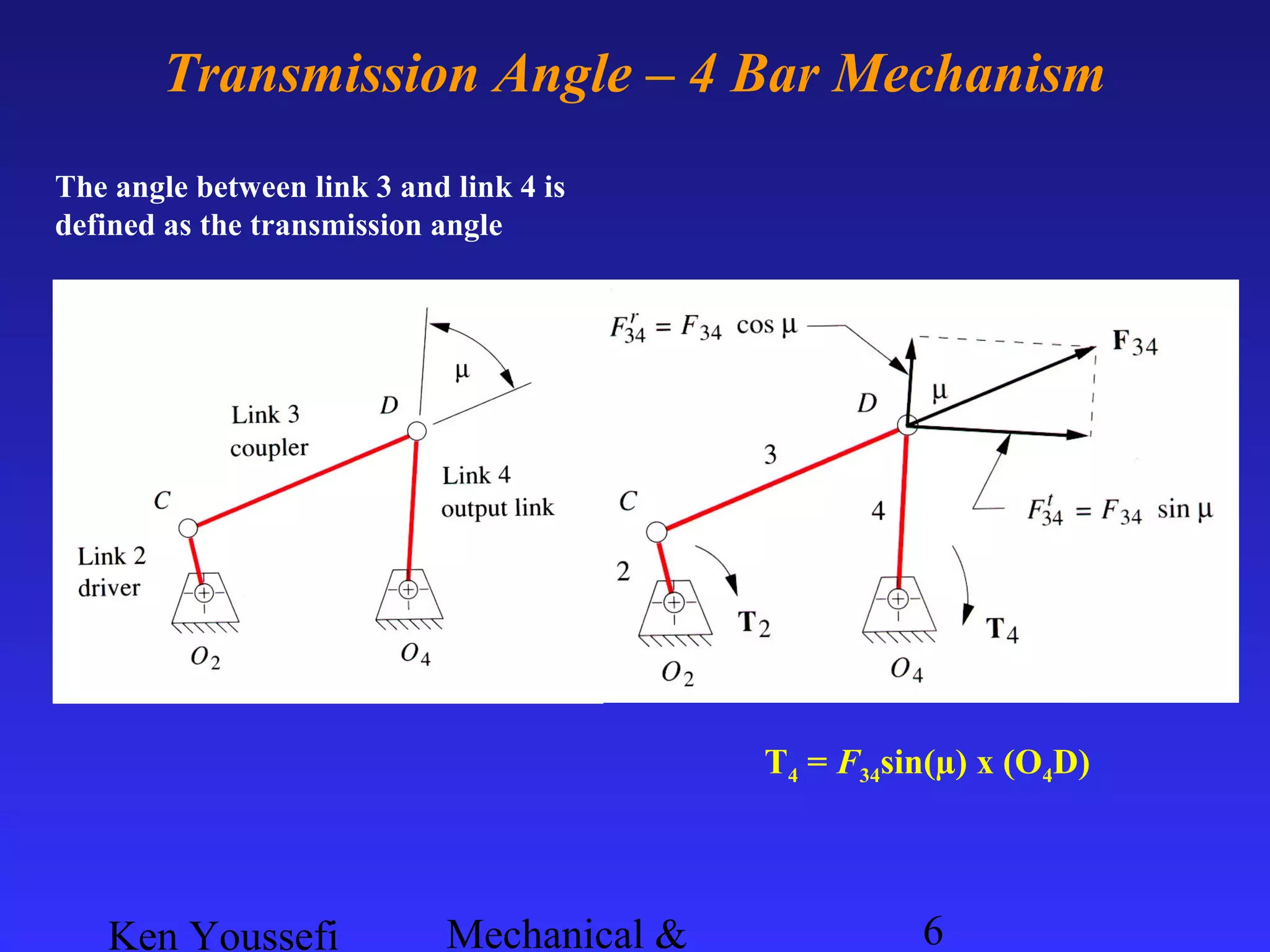
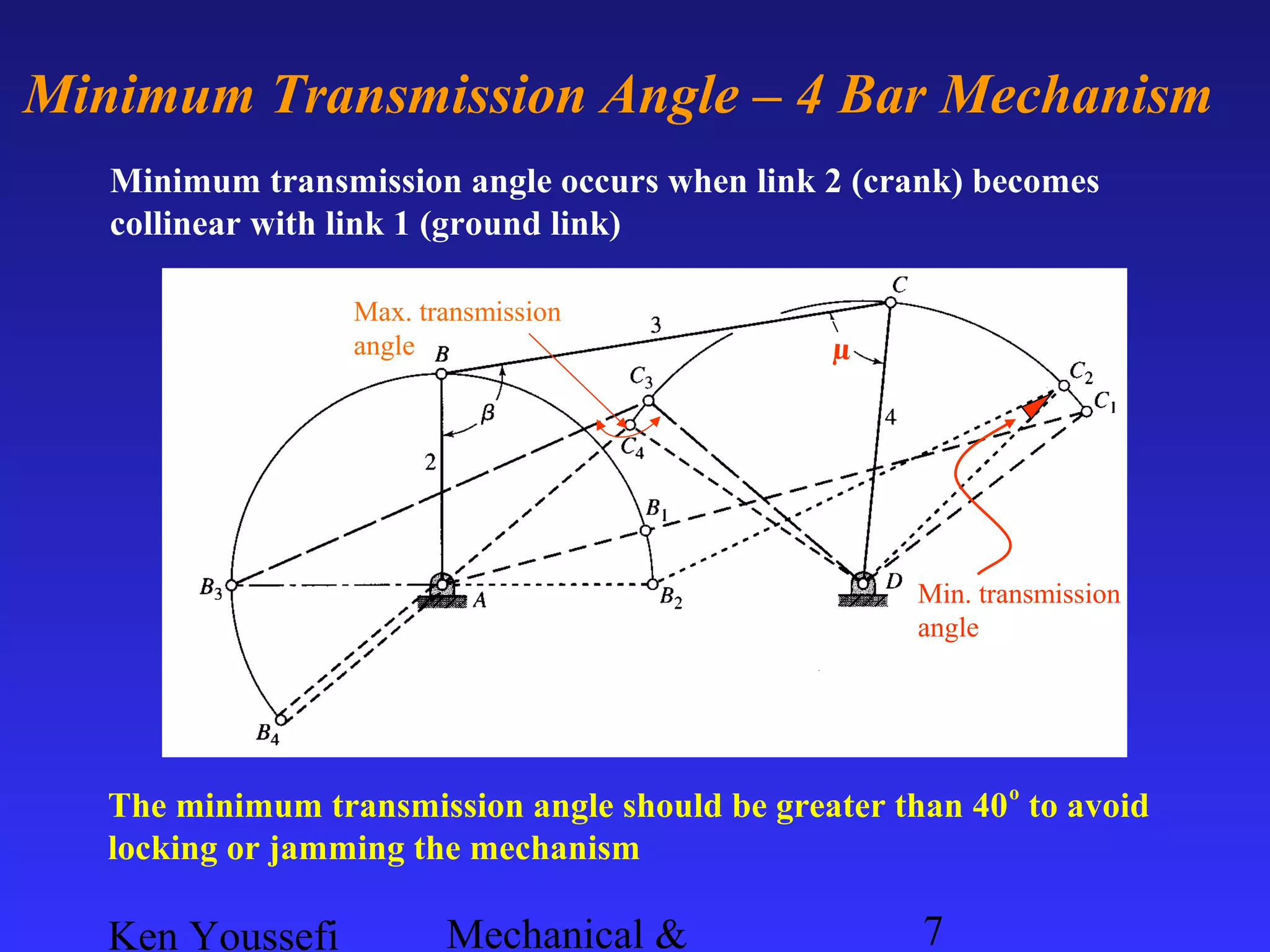
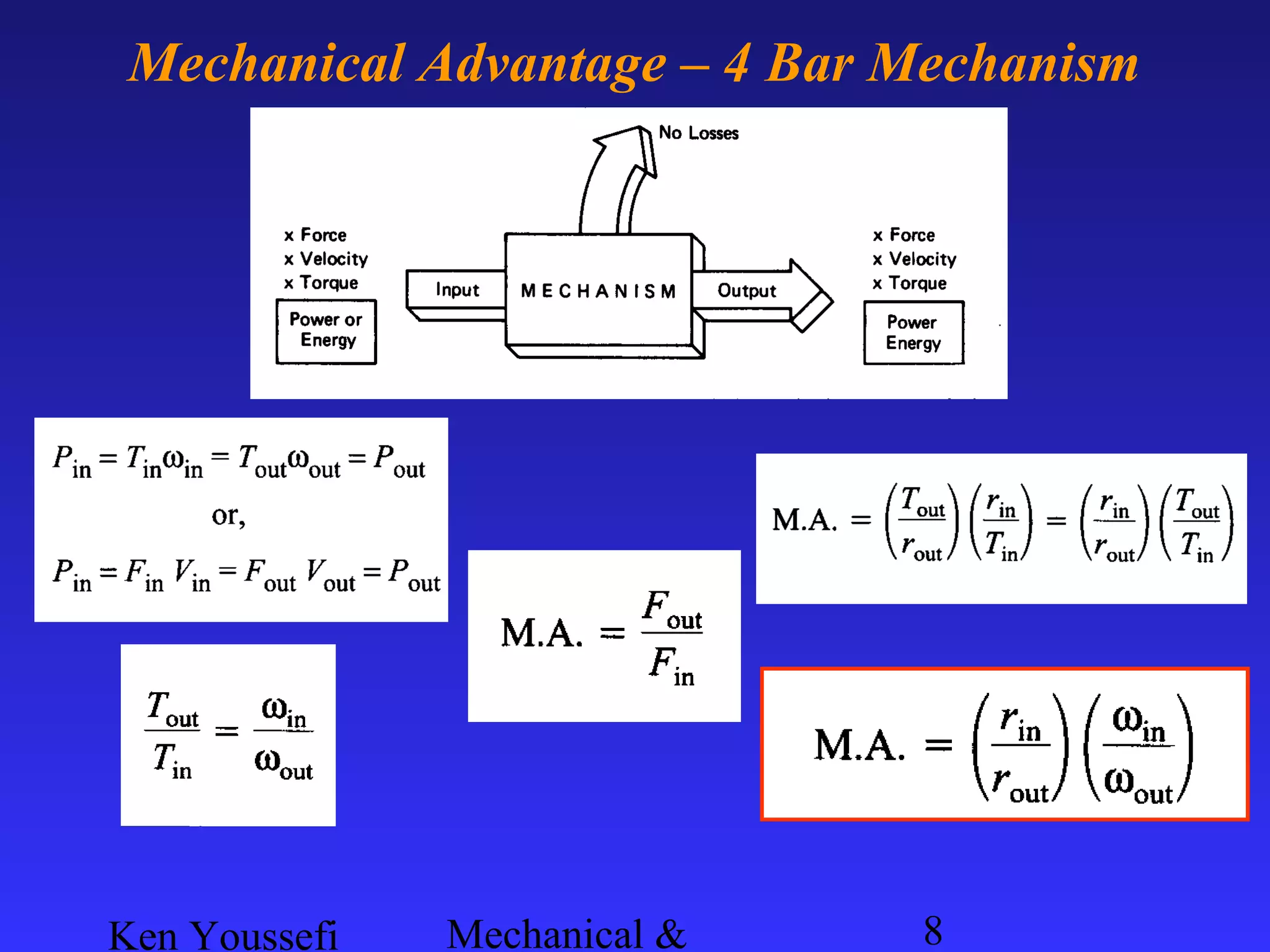
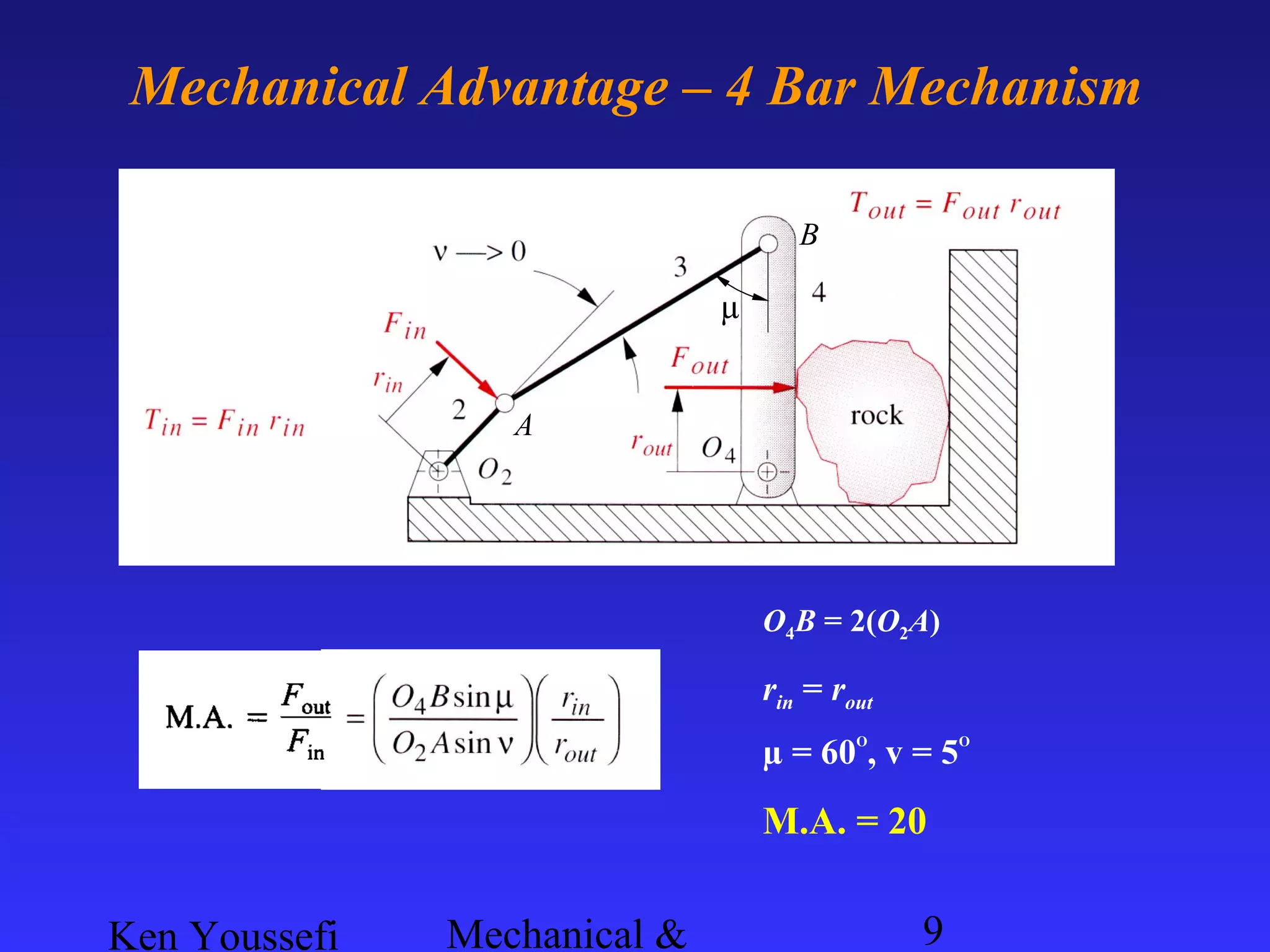
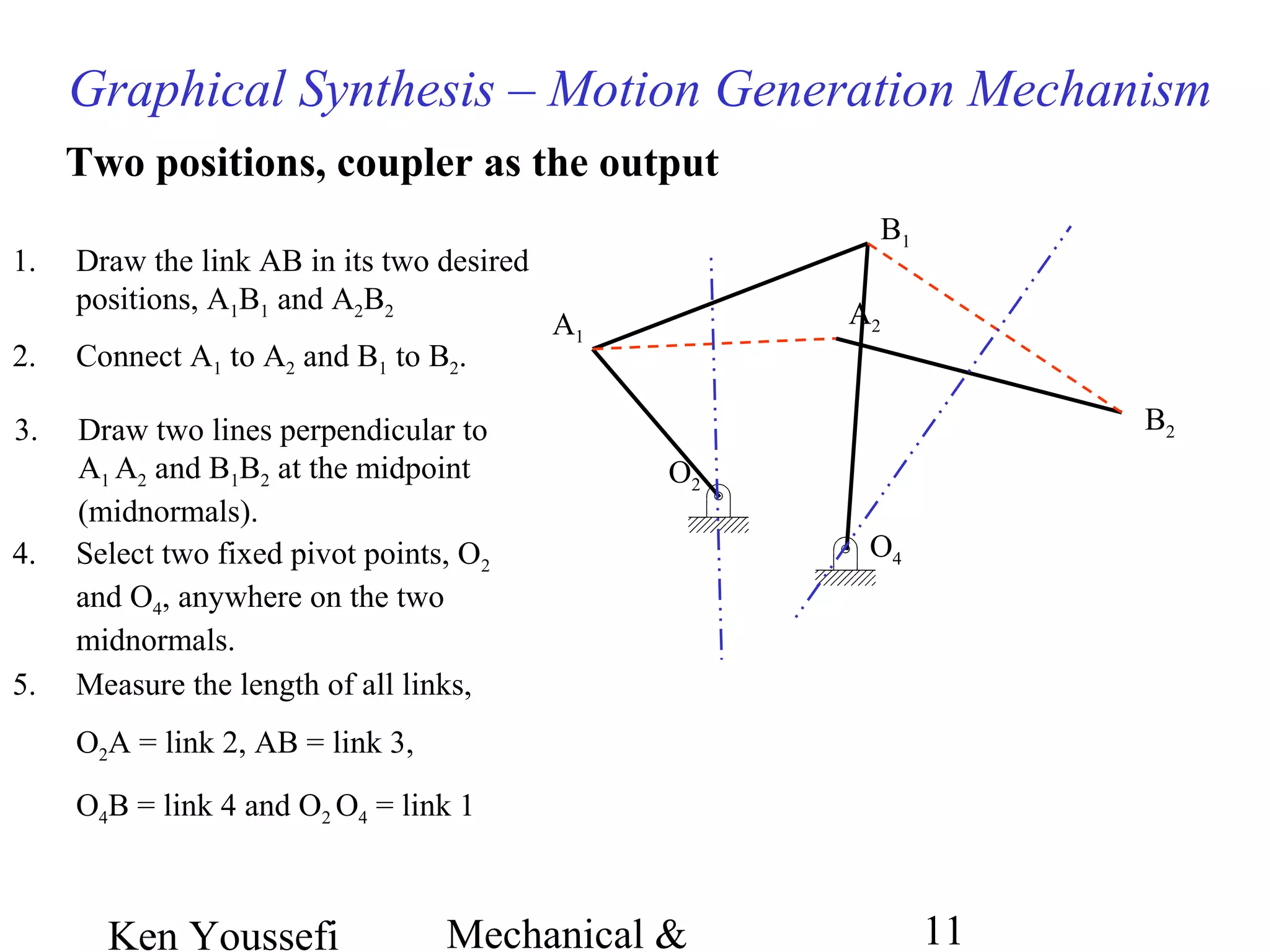
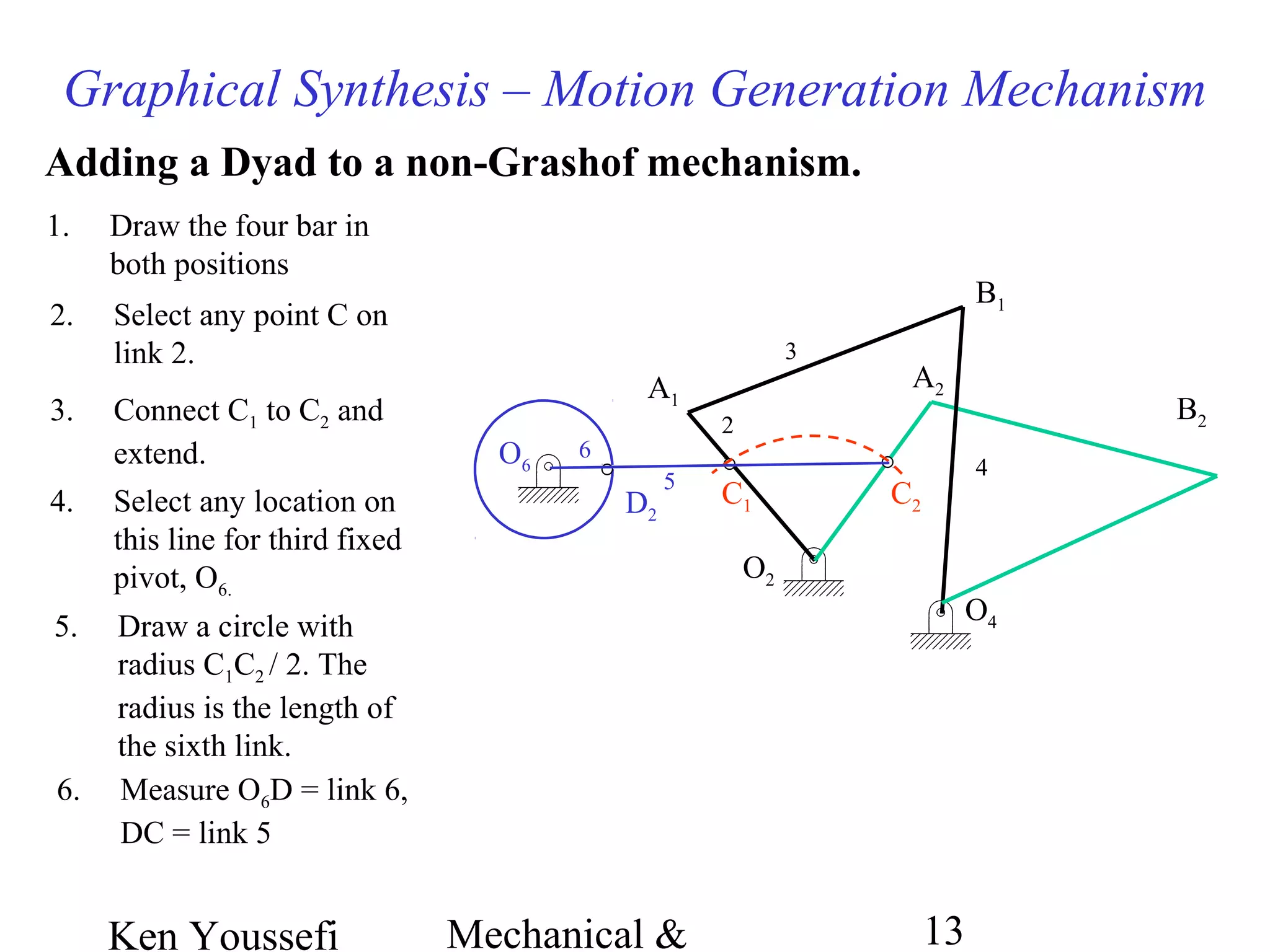
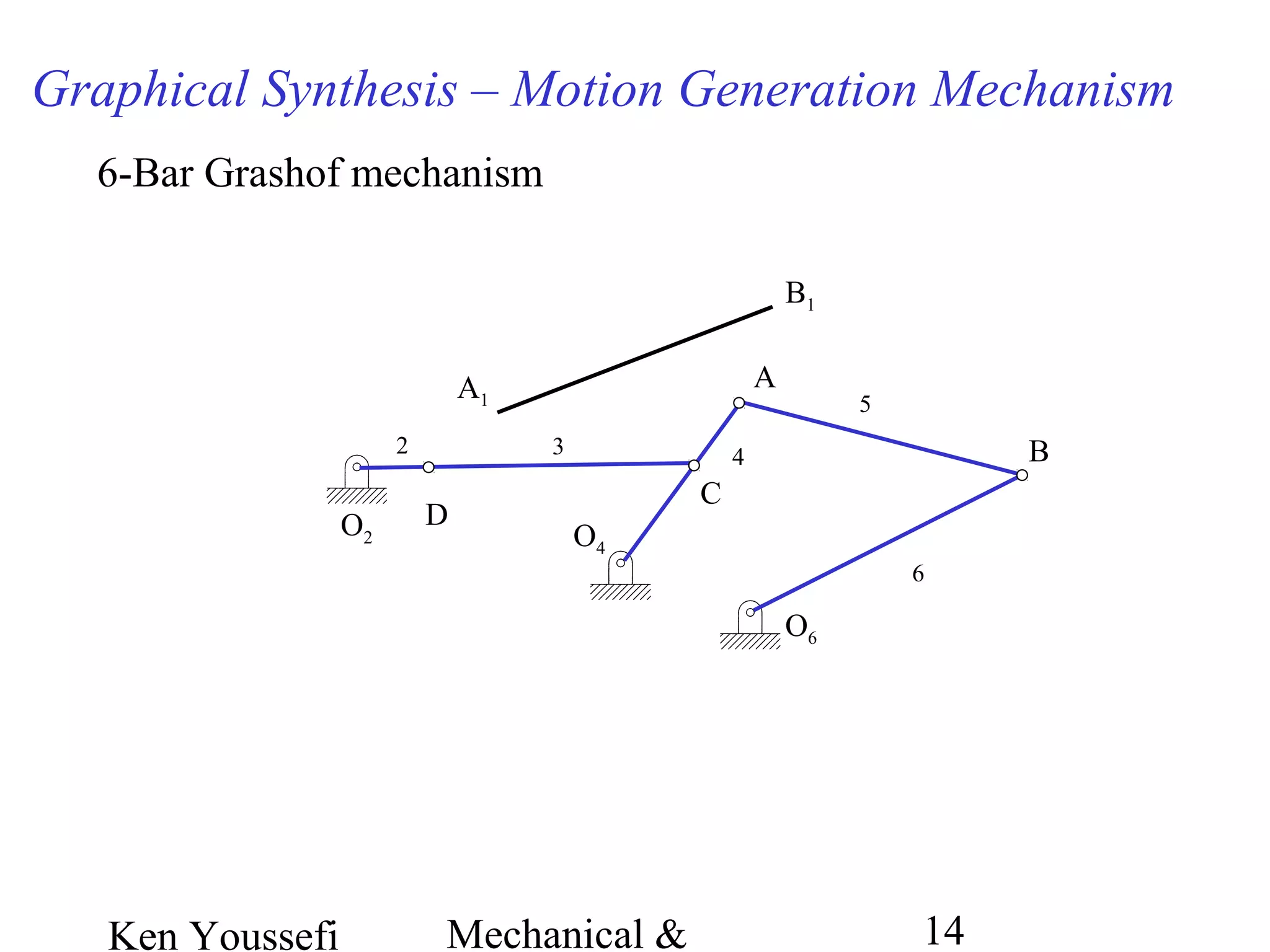
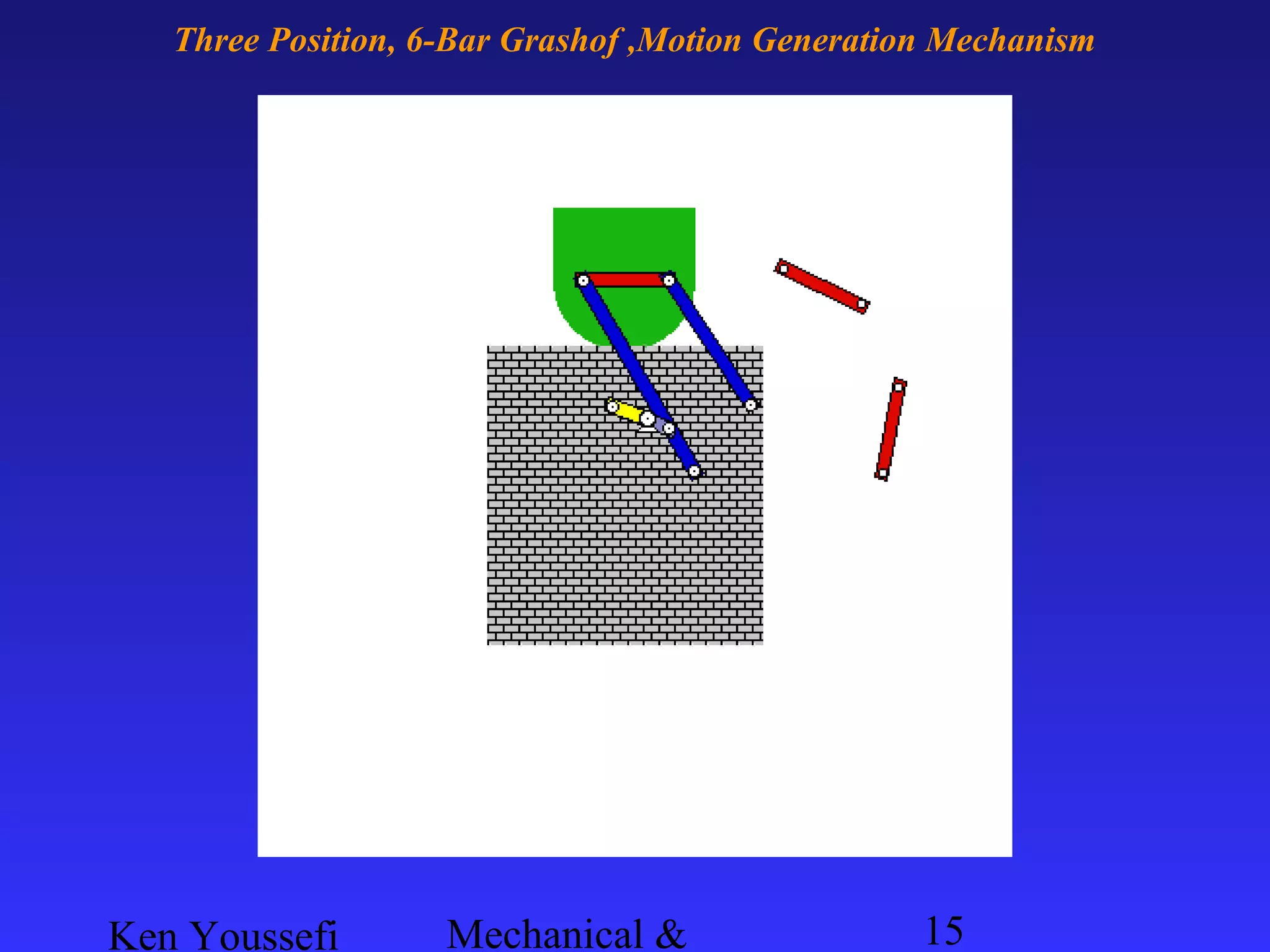
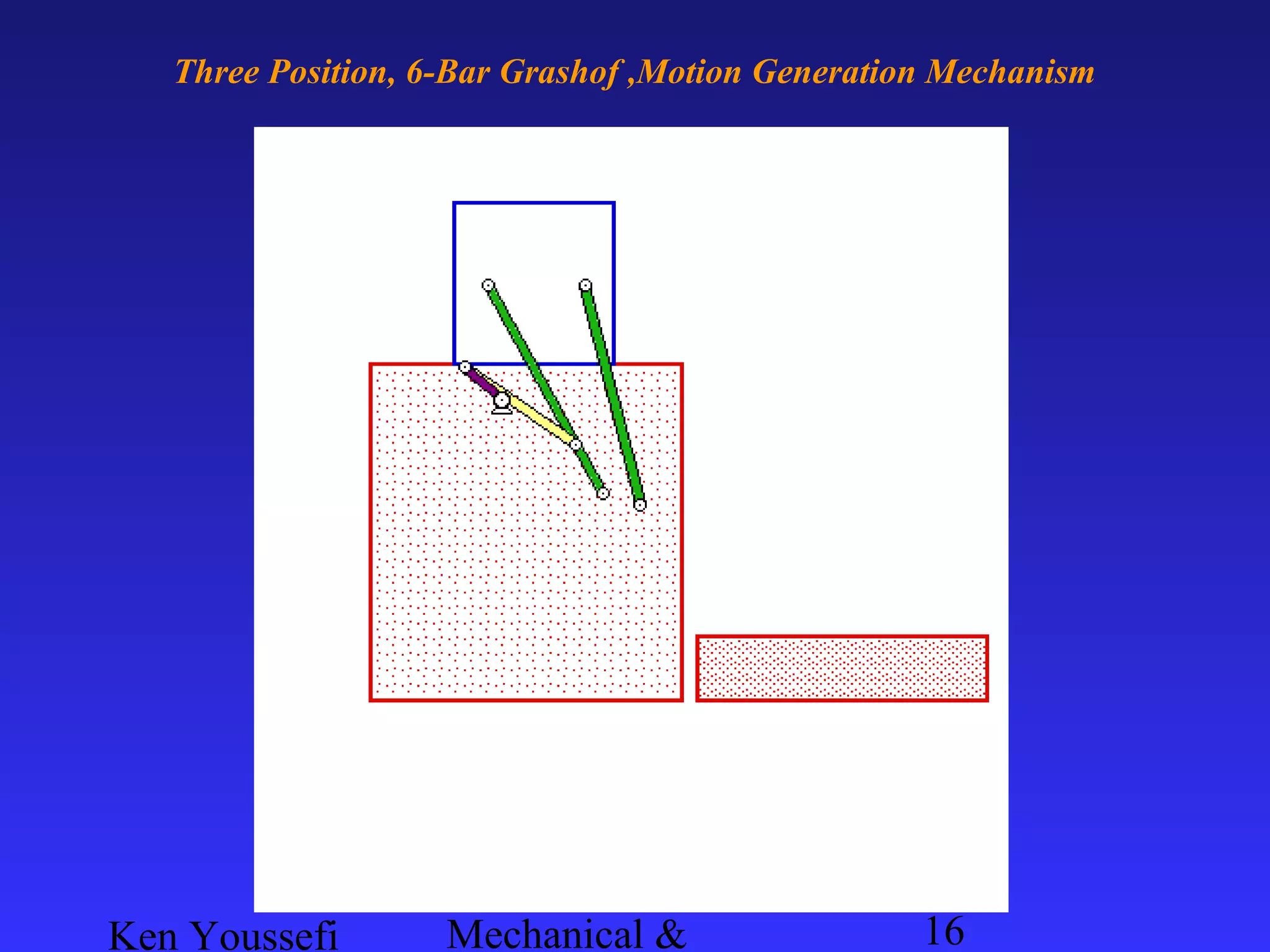
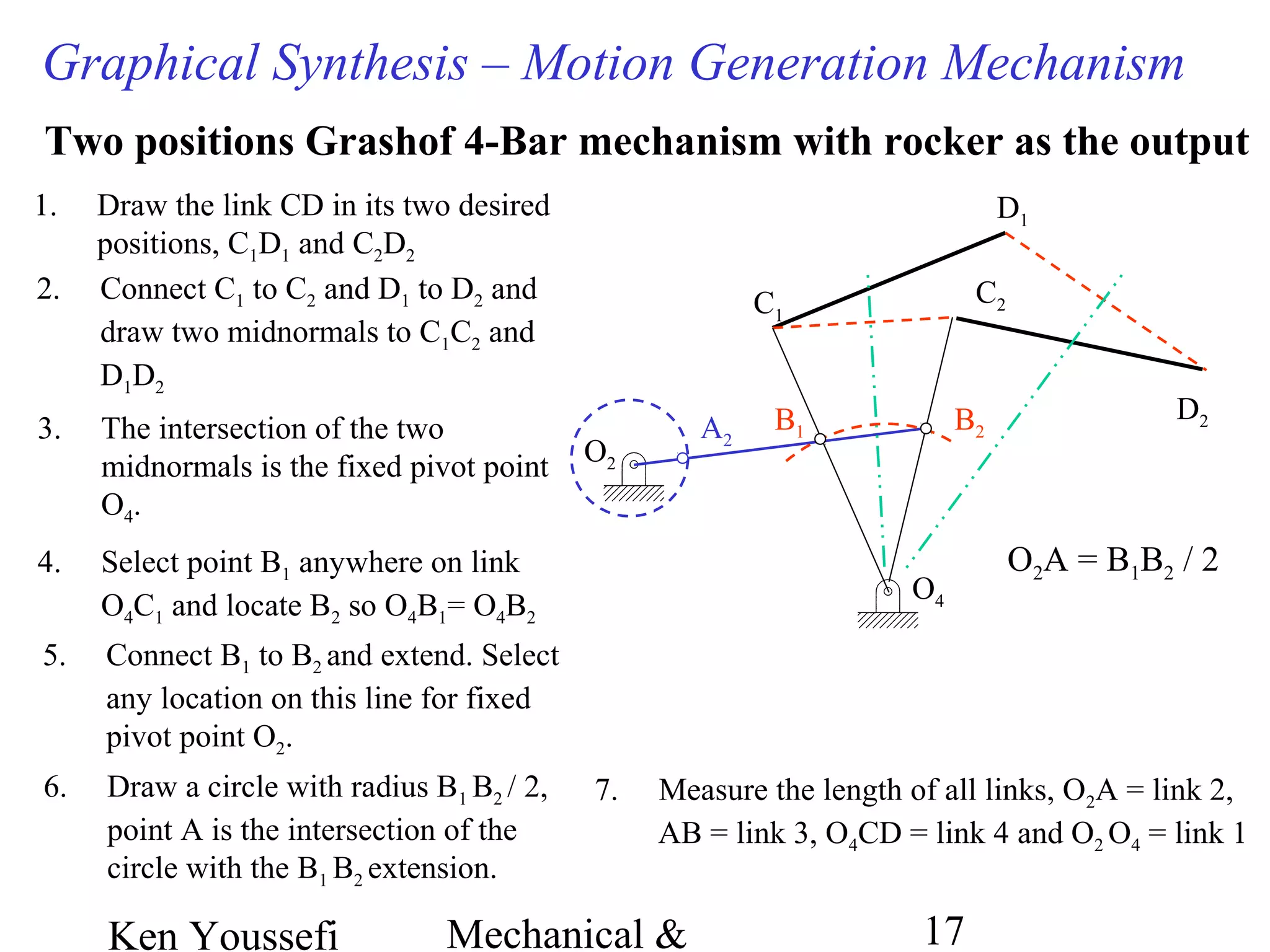
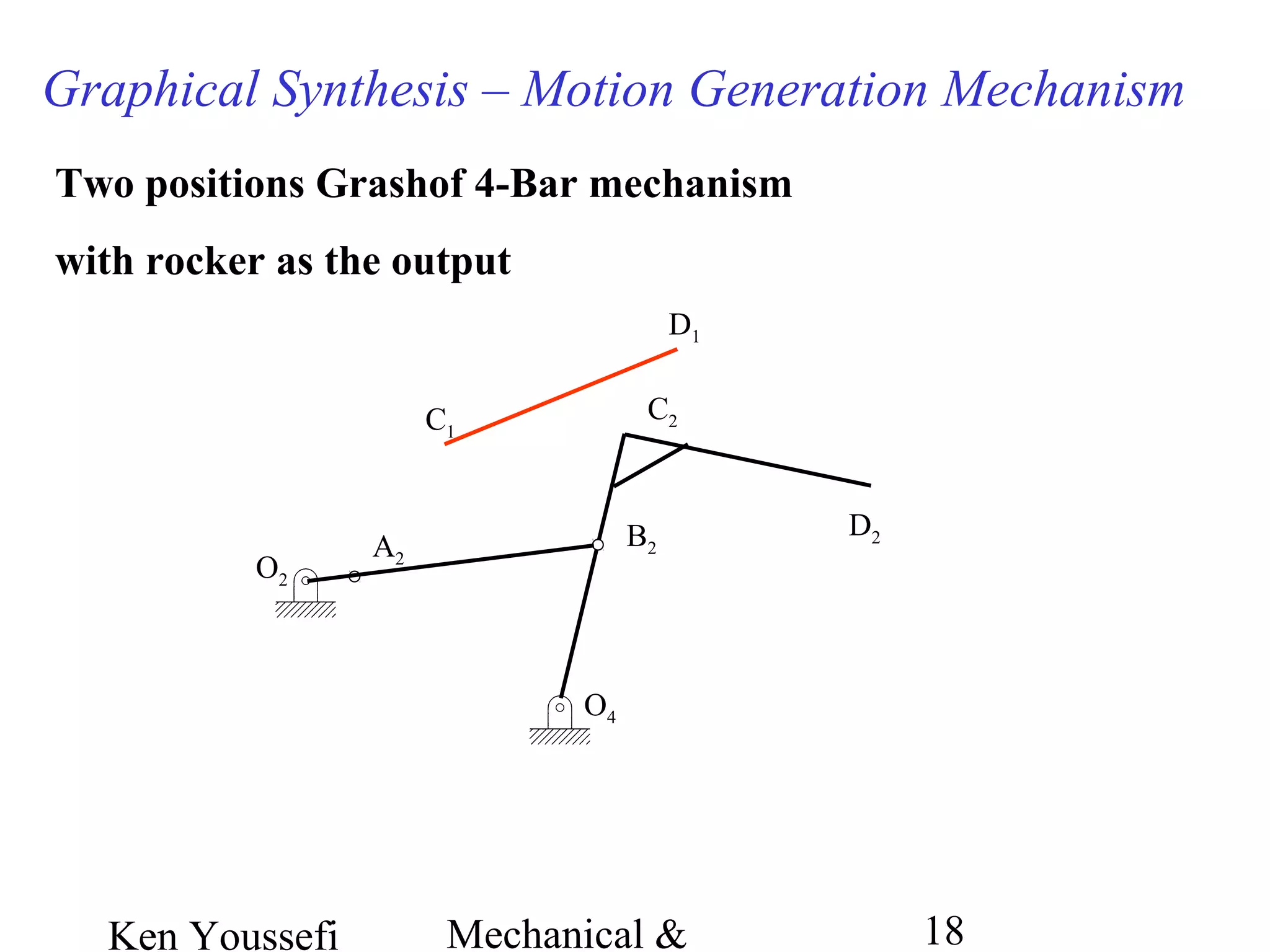
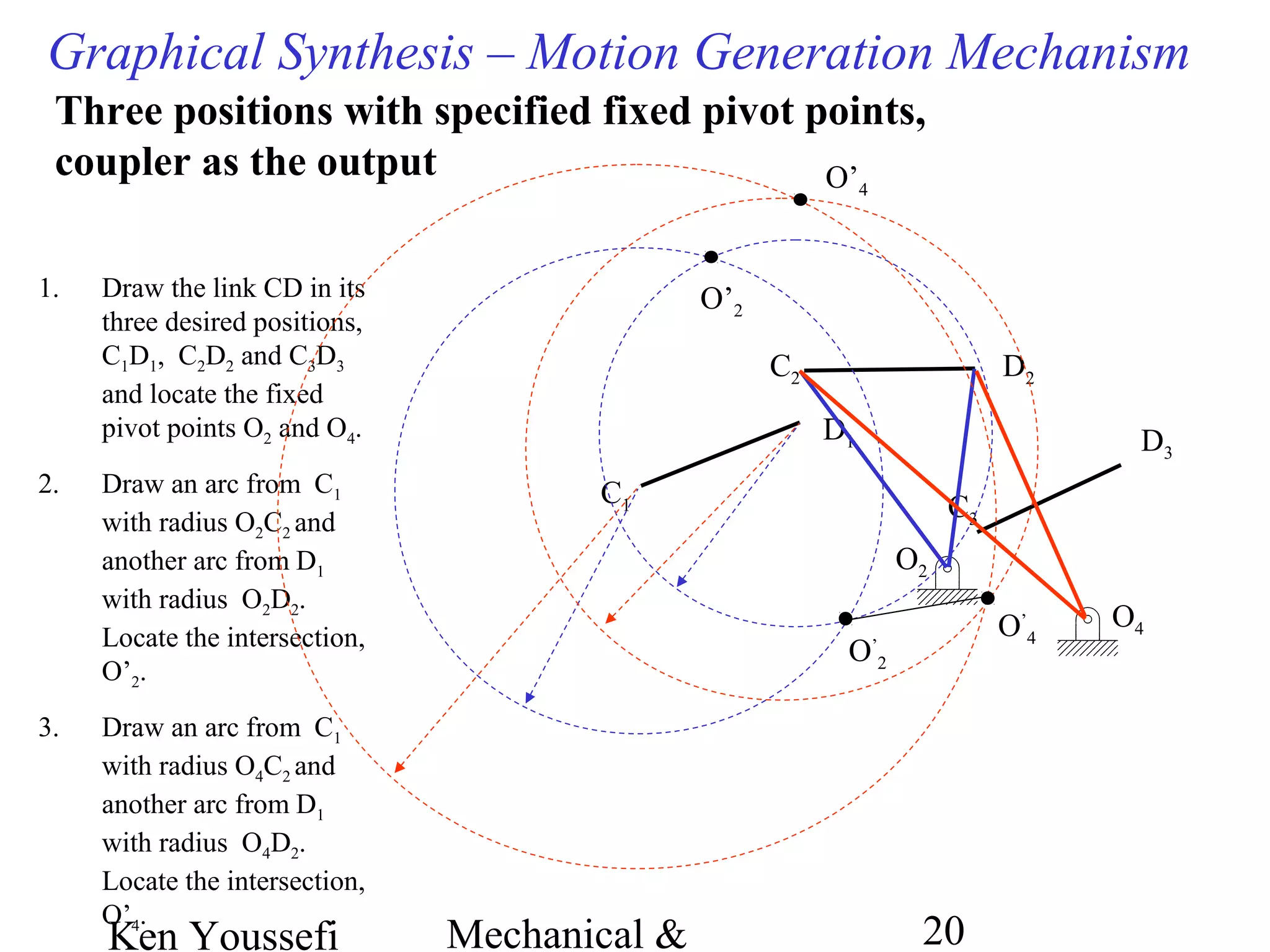
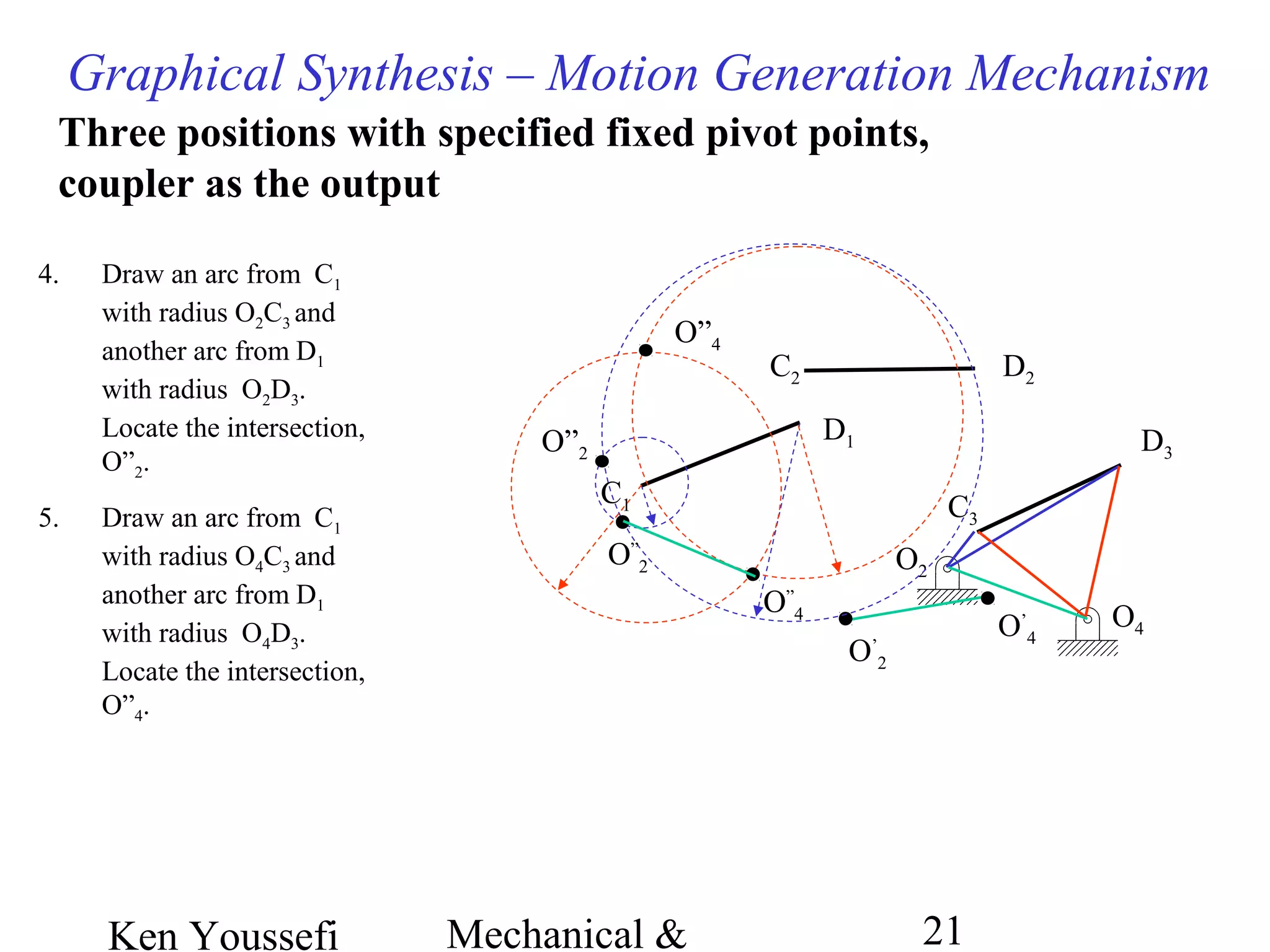
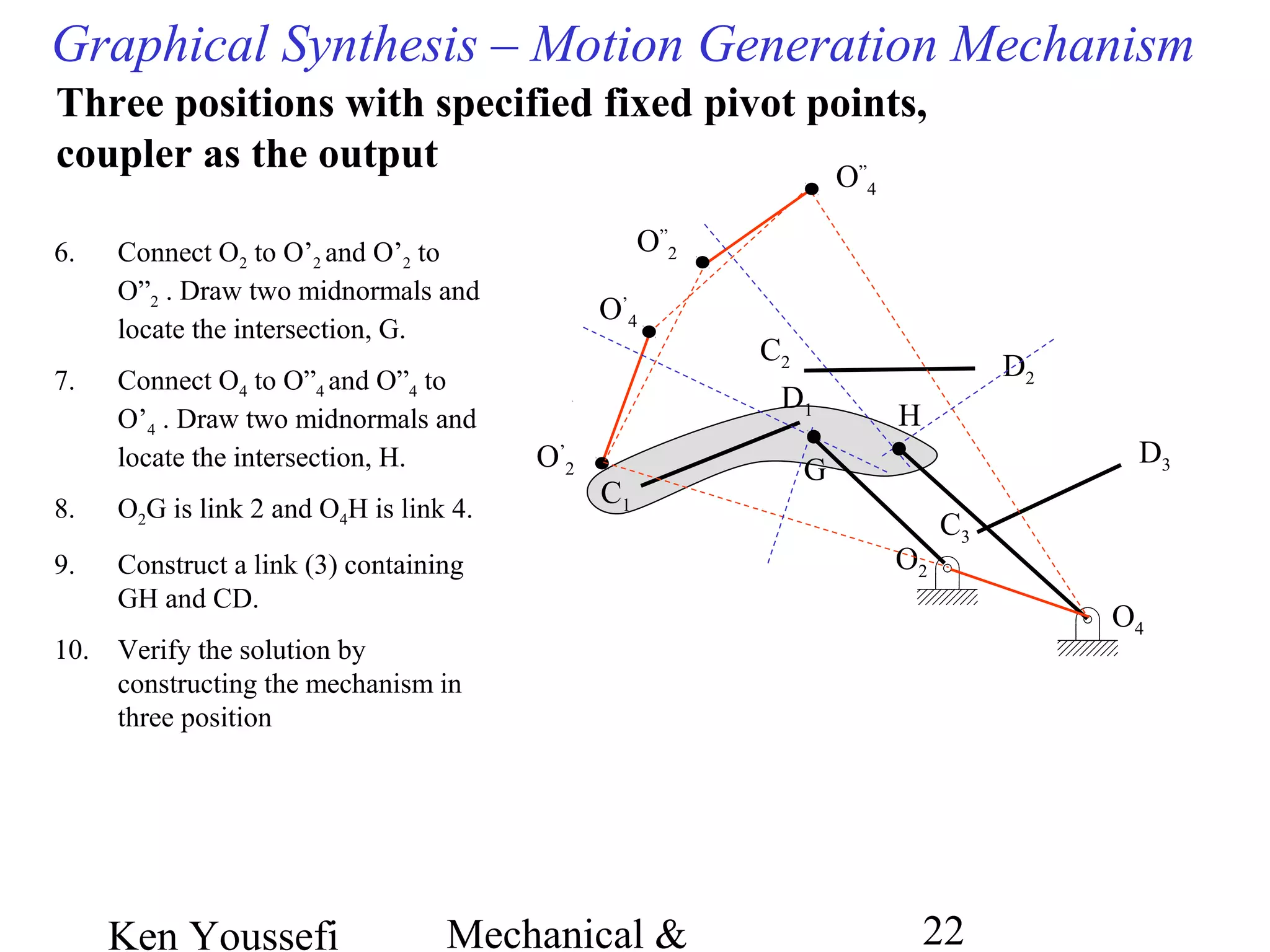
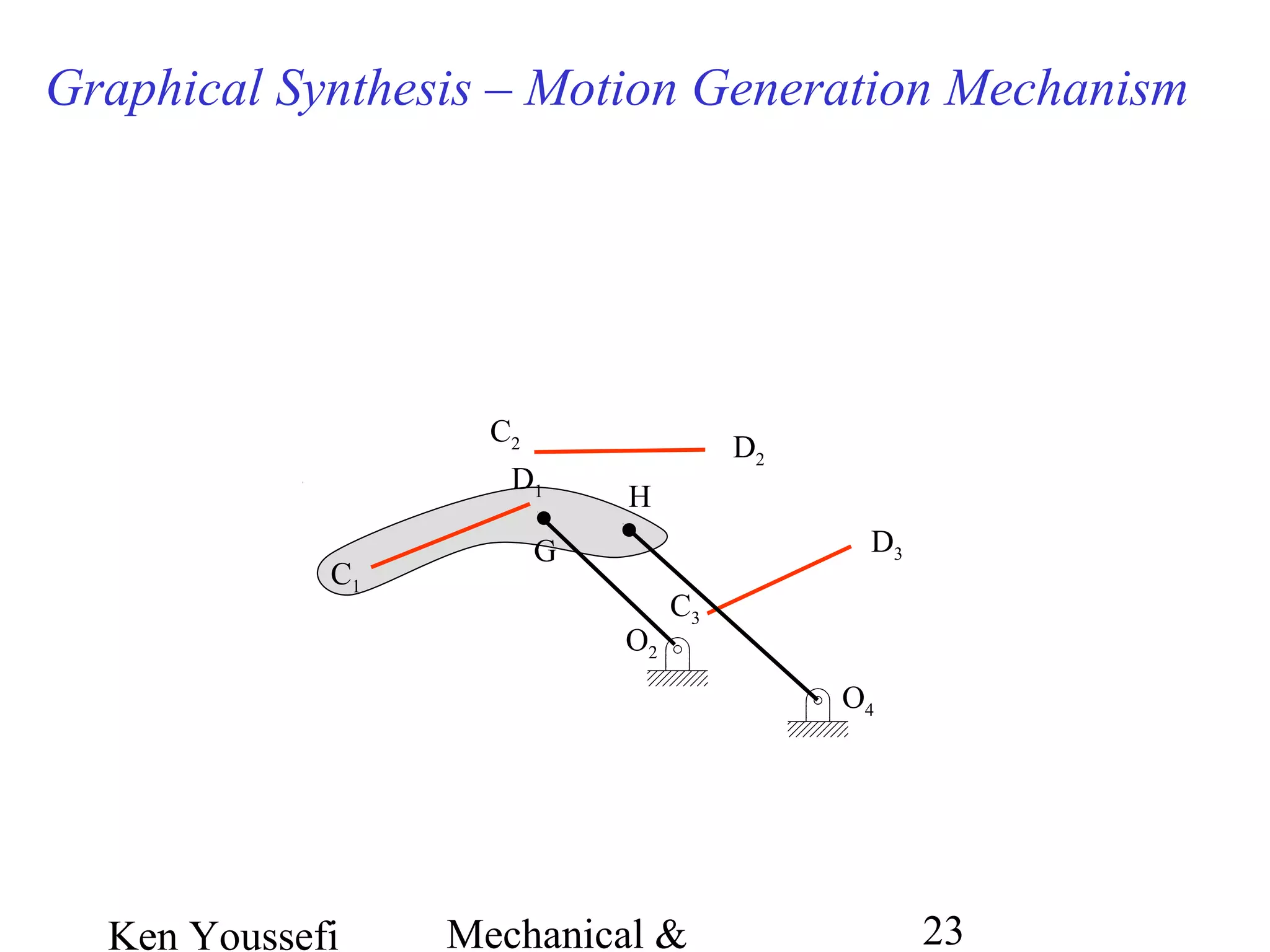
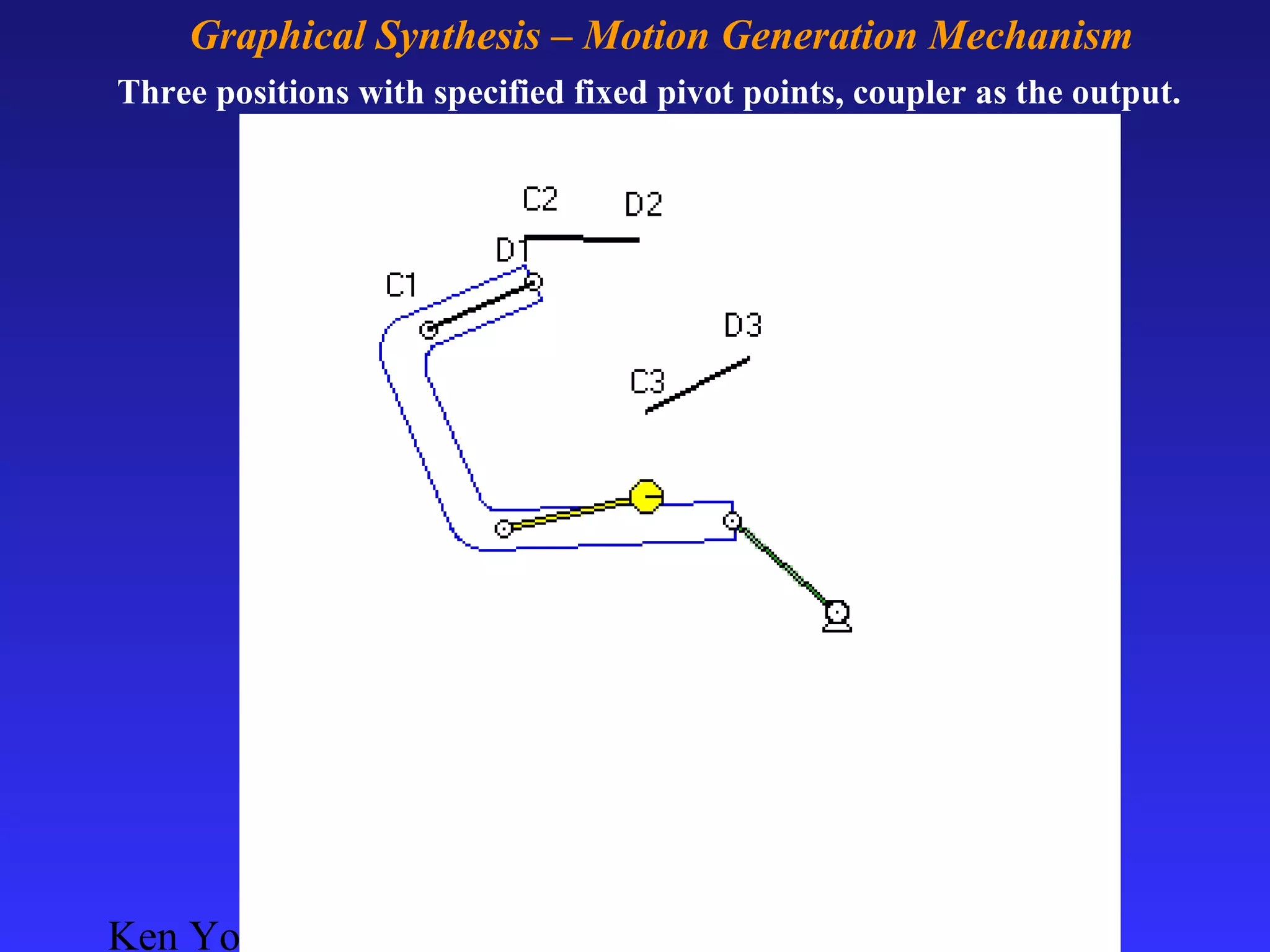
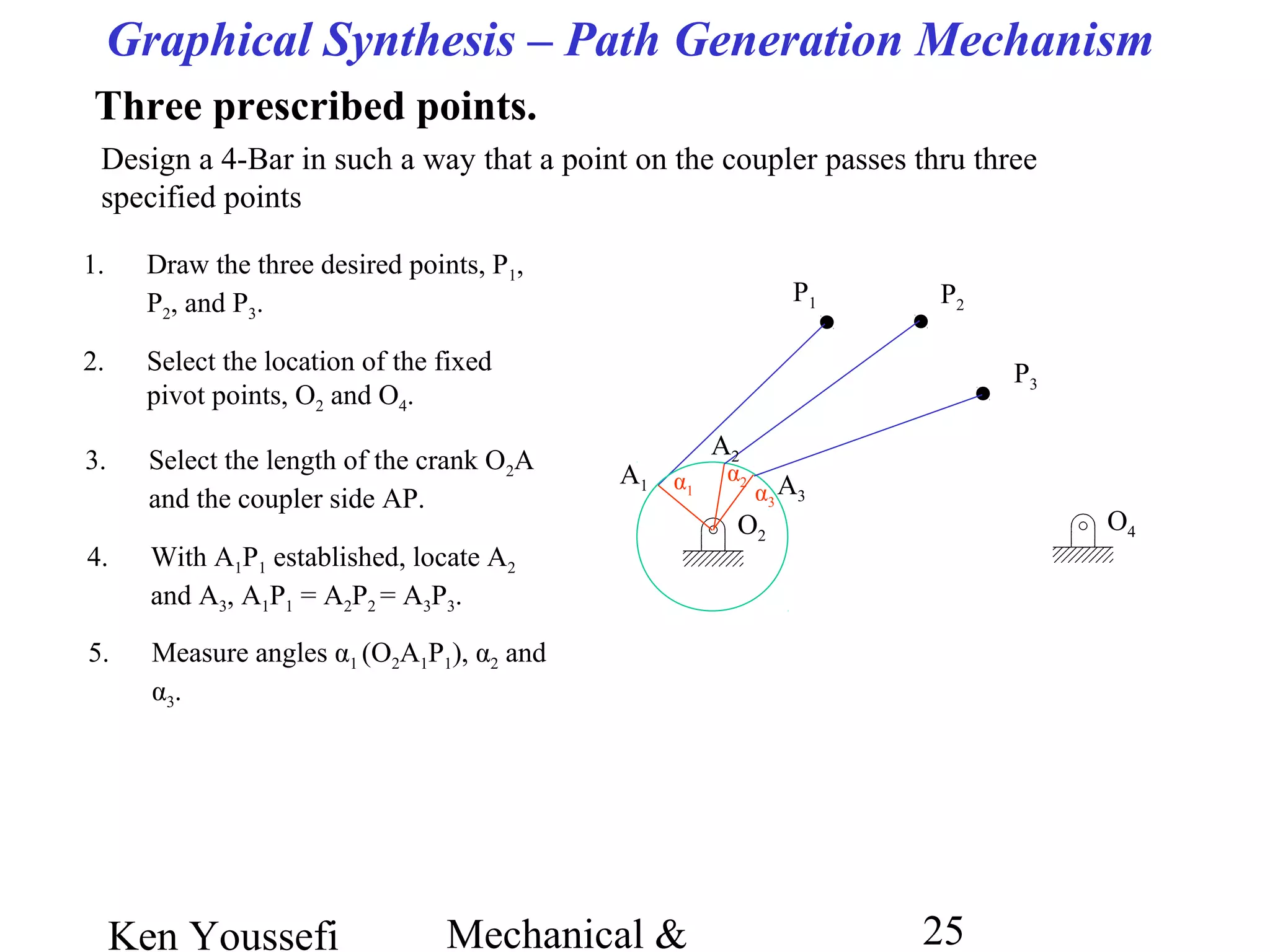
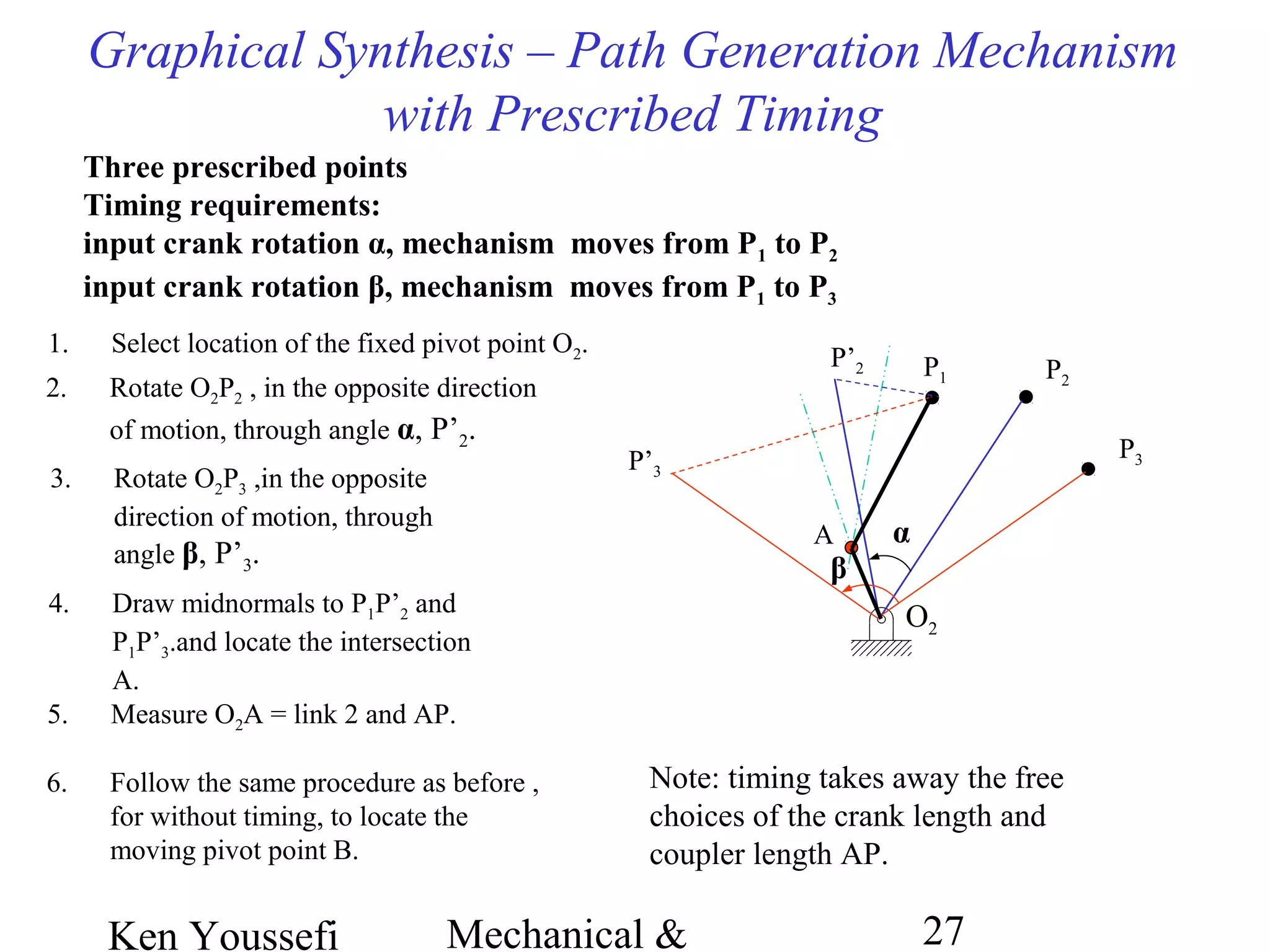
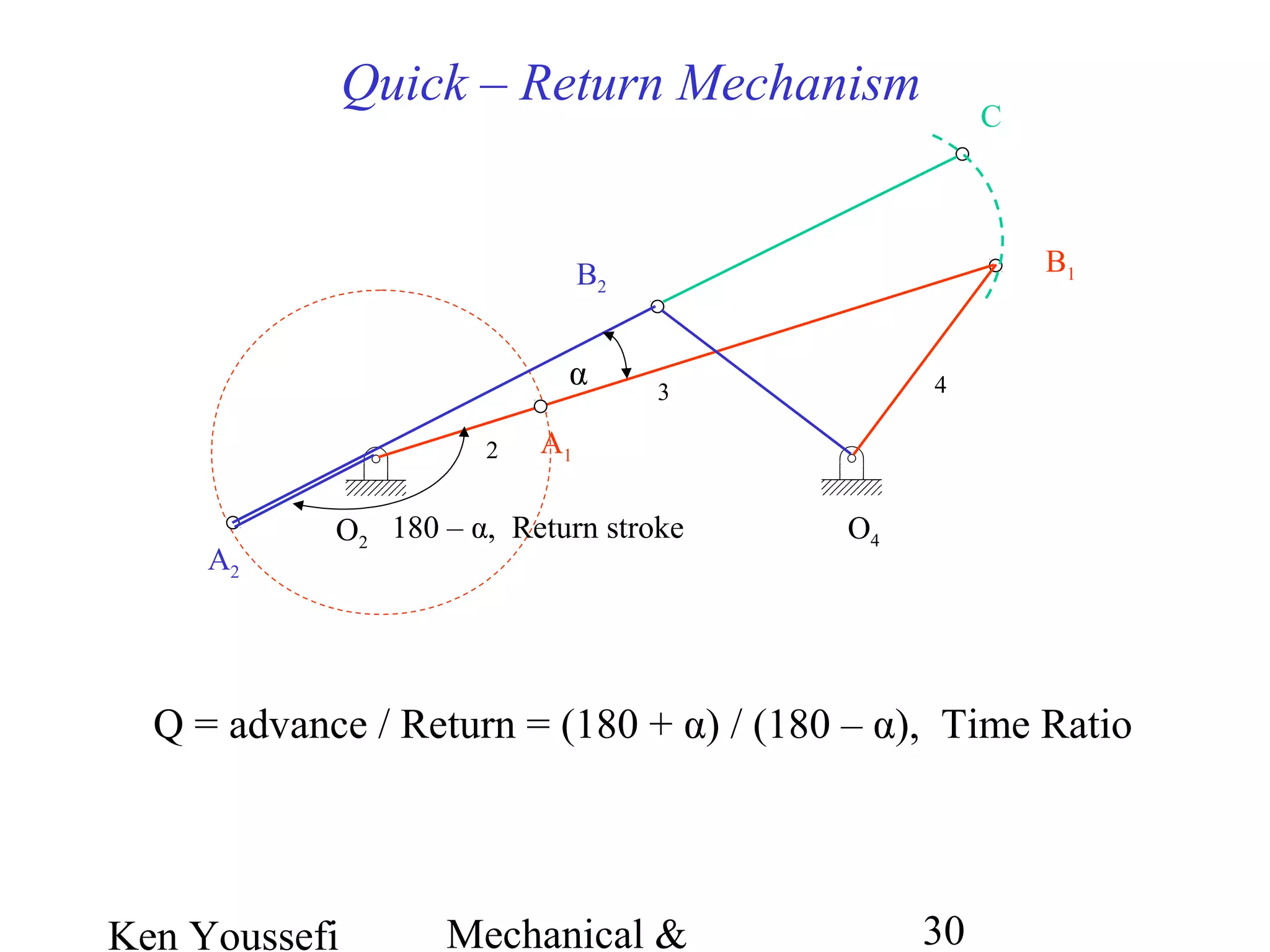
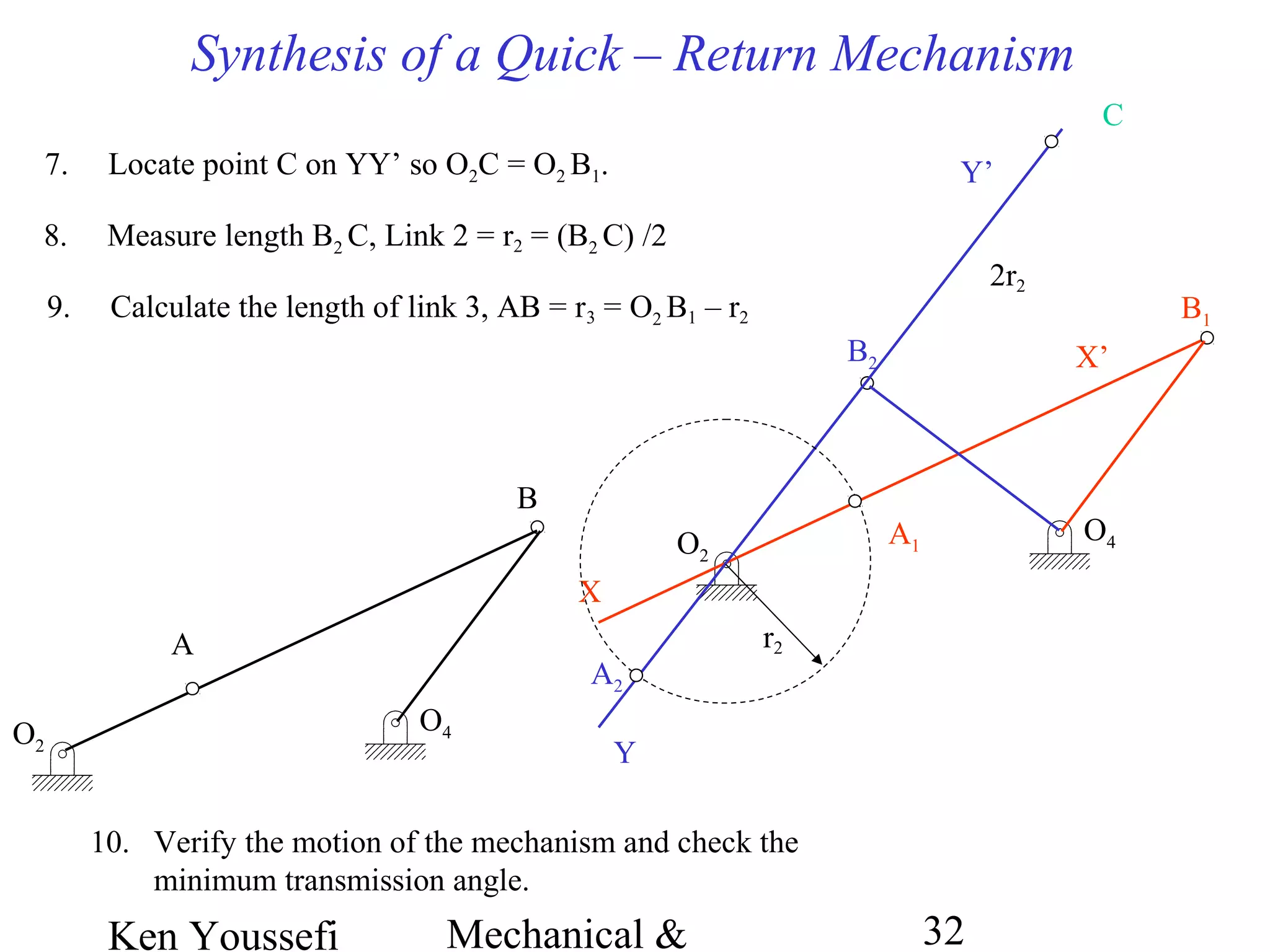
This document provides information on mechanism synthesis and graphical methods for designing mechanisms. It discusses dimensional, number, and type synthesis to design mechanisms for specified motions. Graphical methods are presented for generating both motion and path generating mechanisms with 4-bar and 6-bar linkages using coupler curves. Steps are provided for graphical synthesis including selecting fixed pivot points, locating link lengths, and verifying mechanism positions. Quick-return mechanisms are also discussed.

1. Ken Youssefi Mechanical & 1
Mechanism Design
Graphical Method

2. Ken Youssefi Mechanical & 2
• Dimensional Synthesis
Mechanism Synthesis
Design a mechanism to obtain a specified
motion or force.
– How many links should the
mechanism have? How many degrees of freedom
are desired?
• Number Synthesis
– given the required performance,
what type of mechanism is suitable? Linkages, gears,
cam and follower, belt and pulley and chain and
sprocket.
• Type Synthesis
– deals with determining
the length of all links, gear diameter, cam profile.

3. Ken Youssefi Mechanical & 3
Mechanism Synthesis
Type Synthesis
The Associated Linkage Concept
It is desired to derive various types of mechanisms for driving a
slider with a linear translation along a fixed path in a machine.
Also, assume that the slider must move with a reciprocating
motion.
4-Bar

4. Ken Youssefi Mechanical & 4
Mechanism Synthesis
Type Synthesis - The Associated Linkage Concept (6-Bar)
6-Bar

5. Ken Youssefi Mechanical & 5
Limiting Conditions – 4 Bar Mechanism
Toggle positions of a crank-rocker mechanism. Links 2 and 3
become collinear.

6. Ken Youssefi Mechanical & 6
Transmission Angle – 4 Bar Mechanism
The angle between link 3 and link 4 is
defined as the transmission angle
T4 = F34sin(µ) x (O4D)

7. Ken Youssefi Mechanical & 7
Minimum Transmission Angle – 4 Bar Mechanism
Minimum transmission angle occurs when link 2 (crank) becomes
collinear with link 1 (ground link)
The minimum transmission angle should be greater than 40
o
to avoid
locking or jamming the mechanism
µ
Min. transmission
angle
Max. transmission
angle

8. Ken Youssefi Mechanical & 8
Mechanical Advantage – 4 Bar Mechanism

9. Ken Youssefi Mechanical & 9
Mechanical Advantage – 4 Bar Mechanism
O4B = 2(O2A)
rin = rout
µ = 60O
, v = 5O
M.A. = 20
µ
A
B

10. Ken Youssefi Mechanical & 10
Mechanism Synthesis
Dimensional Synthesis
Graphical Methods – provide the designer with
a quick straightforward method but parameters
cannot easily be manipulated to create new
solutions.
– this approach is suitable
for automatic computation. Once a mechanism is
modeled and coded for computer, parameters are
easily manipulated to create new designs.
Analytical Methods

11. Ken Youssefi Mechanical & 11
O2
O44. Select two fixed pivot points, O2
and O4, anywhere on the two
midnormals.
Graphical Synthesis – Motion Generation Mechanism
Two positions, coupler as the output
A1
A2
B1
B2
1. Draw the link AB in its two desired
positions, A1B1 and A2B2
5. Measure the length of all links,
O2A = link 2, AB = link 3,
O4B = link 4 and O2 O4 = link 1
2. Connect A1 to A2 and B1 to B2.
3. Draw two lines perpendicular to
A1 A2 and B1B2 at the midpoint
(midnormals).

12. Ken Youssefi Mechanical & 12
O4O2
Graphical Synthesis – Motion Generation Mechanism
Three positions, coupler as the output
A1
A2
A3
B1
B2
B3
Same procedure as for two positions.
1. Draw the link AB in three desired
positions.
2. Draw the midnormals to A1A2 and A2A3,
the intersection locates the fixed pivot
point O2. Same for point B to obtain
second pivot point O4.
3. Check the accuracy of the mechanism,
Grashof condition and the transmission
angle.
4. Change the second position of link
AB to vary the locations of the fixed
points

13. Ken Youssefi Mechanical & 13
O6
4. Select any location on
this line for third fixed
pivot, O6.
D2
5. Draw a circle with
radius C1C2 / 2. The
radius is the length of
the sixth link.
Graphical Synthesis – Motion Generation Mechanism
Adding a Dyad to a non-Grashof mechanism.
A1
A2
B1
B2
O2
O4
2
3
4
1. Draw the four bar in
both positions
C1 C2
2. Select any point C on
link 2.
3. Connect C1 to C2 and
extend.
5
6
6. Measure O6D = link 6,
DC = link 5

14. Ken Youssefi Mechanical & 14
Graphical Synthesis – Motion Generation Mechanism
A1
A
B1
O4
O6
C
DO2
B32 4
5
6
6-Bar Grashof mechanism

15. Ken Youssefi Mechanical & 15
Three Position, 6-Bar Grashof ,Motion Generation Mechanism

16. Ken Youssefi Mechanical & 16
Three Position, 6-Bar Grashof ,Motion Generation Mechanism

17. Ken Youssefi Mechanical & 17
Graphical Synthesis – Motion Generation Mechanism
Two positions Grashof 4-Bar mechanism with rocker as the output
D1
C1
C2
D2
O2
5. Connect B1 to B2 and extend. Select
any location on this line for fixed
pivot point O2.
O2A = B1B2 / 2
7. Measure the length of all links, O2A = link 2,
AB = link 3, O4CD = link 4 and O2 O4 = link 1
1. Draw the link CD in its two desired
positions, C1D1 and C2D2
2. Connect C1 to C2 and D1 to D2 and
draw two midnormals to C1C2 and
D1D2
O4
3. The intersection of the two
midnormals is the fixed pivot point
O4.
B1 B2
4. Select point B1 anywhere on link
O4C1 and locate B2 so O4B1= O4B2
A2
6. Draw a circle with radius B1 B2 / 2,
point A is the intersection of the
circle with the B1 B2 extension.

18. Ken Youssefi Mechanical & 18
Graphical Synthesis – Motion Generation Mechanism
Two positions Grashof 4-Bar mechanism
with rocker as the output
D1
C1
C2
A2
O4
O2
B2
D2

19. Ken Youssefi Mechanical & 19
Two Position, 4-Bar Grashof Motion Generation Mechanism

20. Ken Youssefi Mechanical & 20
Graphical Synthesis – Motion Generation Mechanism
Three positions with specified fixed pivot points,
coupler as the output
C1
D1
C2
C3
D2
D3
O4
O2
1. Draw the link CD in its
three desired positions,
C1D1, C2D2 and C3D3
and locate the fixed
pivot points O2 and O4.
2. Draw an arc from C1
with radius O2C2 and
another arc from D1
with radius O2D2.
Locate the intersection,
O’2.
3. Draw an arc from C1
with radius O4C2 and
another arc from D1
with radius O4D2.
Locate the intersection,
O’4.
O’
4
O’
2
O’2
O’4

21. Ken Youssefi Mechanical & 21
Graphical Synthesis – Motion Generation Mechanism
C1
D1
C2
C3
D2
D3
O4
O2
O’
2
O’
4
Three positions with specified fixed pivot points,
coupler as the output
4. Draw an arc from C1
with radius O2C3 and
another arc from D1
with radius O2D3.
Locate the intersection,
O”2.
5. Draw an arc from C1
with radius O4C3 and
another arc from D1
with radius O4D3.
Locate the intersection,
O”4.
O”
2
O”
4
O”2
O”4

22. Ken Youssefi Mechanical & 22
C1
D1
C2
C3
D2
O4
O2
O”
2
O”
4
O’
2
O’
4
G
H
Graphical Synthesis – Motion Generation Mechanism
Three positions with specified fixed pivot points,
coupler as the output
D3
6. Connect O2 to O’2 and O’2 to
O”2 . Draw two midnormals and
locate the intersection, G.
7. Connect O4 to O”4 and O”4 to
O’4 . Draw two midnormals and
locate the intersection, H.
8. O2G is link 2 and O4H is link 4.
9. Construct a link (3) containing
GH and CD.
10. Verify the solution by
constructing the mechanism in
three position

23. Ken Youssefi Mechanical & 23
Graphical Synthesis – Motion Generation Mechanism
C1
D1
C2
C3
D2
O4
O2
G
H
D3

24. Ken Youssefi Mechanical & 24
Graphical Synthesis – Motion Generation Mechanism
Three positions with specified fixed pivot points, coupler as the output.

25. Ken Youssefi Mechanical & 25
O4O2
2. Select the location of the fixed
pivot points, O2 and O4.
Graphical Synthesis – Path Generation Mechanism
Three prescribed points.
5. Measure angles α1 (O2A1P1), α2 and
α3.
α1
α2
α3
P1 P2
P3
1. Draw the three desired points, P1,
P2, and P3.
A1
3. Select the length of the crank O2A
and the coupler side AP. A3
A2
4. With A1P1 established, locate A2
and A3, A1P1 = A2P2 = A3P3.
Design a 4-Bar in such a way that a point on the coupler passes thru three
specified points

26. Ken Youssefi Mechanical & 26
Graphical Synthesis – Path Generation Mechanism
Three prescribed points.
Locate moving pivot B by means of kinematic inversion. Fix coupler AP in
position 1 and rotate O2O4.
O4
O2
P1 P2
P3
A1
11. Verify the mechanism.
B
O”4
O’2
6. Rotate A1O2 about A1 by (α2
– α1) to O’2 .
O’4
7. Draw an arc from O’2 with radius
O2O4 , draw another arc from P1 with
radius P2O4 , locate the intersection,
O’4 .
O”2
8. Rotate A1O2 about A1 by (α3 – α1)
to O”2 .
9. Draw an arc from O”2 with radius
O2O4 , draw another arc from P1
with radius P3O4 , locate the
intersection, O”4 .
10. Connect O4 to O’4 and O’4 to O”4
and draw the midnormals. Locate
the intersection, B.

27. Ken Youssefi Mechanical & 27
O2
1. Select location of the fixed pivot point O2.
Graphical Synthesis – Path Generation Mechanism
with Prescribed Timing
Three prescribed points
Timing requirements:
input crank rotation α, mechanism moves from P1 to P2
input crank rotation β, mechanism moves from P1 to P3
P1 P2
P3
6. Follow the same procedure as before ,
for without timing, to locate the
moving pivot point B.
A
Note: timing takes away the free
choices of the crank length and
coupler length AP.
P’2
α
2. Rotate O2P2 , in the opposite direction
of motion, through angle α, P’2.
P’3
β
3. Rotate O2P3 ,in the opposite
direction of motion, through
angle β, P’3.
4. Draw midnormals to P1P’2 and
P1P’3.and locate the intersection
A.
5. Measure O2A = link 2 and AP.

28. Ken Youssefi Mechanical & 28
Graphical Synthesis; Quick – Return Mechanism
Q = time of advance stroke / time of return stroke
Q > 1 quick-return mechanism
Advance stroke – mechanism operates under the load.
Return stroke – mechanism operates under no load.
4-Bar crank-Rocker mechanism

29. Ken Youssefi Mechanical & 29
Quick – Return Mechanism
Consider the two toggle positions of a
crank-rocker mechanism.
O4O2
B1
2
3 4
A1
B2
A2
C
Locate point C to satisfy the following two conditions;
1) C is on extension of line A2B2.
2) O2C = O2B1 = r2 + r3
B2C = r2 +r3 - (r3 – r2) = 2r2
r3
– r2

30. Ken Youssefi Mechanical & 30
Quick – Return Mechanism
O4O2
B1
2
3 4
A1
B2
A2
C
α
180 – α, Return stroke
Q = advance / Return = (180 + α) / (180 – α), Time Ratio

31. Ken Youssefi Mechanical & 31
Synthesis of a Quick – Return Mechanism
Known or selected;
Rocker angle, φ
Rocker length, r4
Time ratio, Q
Determine; r1, r2, r3
O4
1. Select the location for the fixed
pivot point, O4.
O2
6. The intersection of XX’ and YY’ is
the other fixed pivot, O2
X
4. Construct an arbitrary line XX’
through point B1.
X’
5. Construct the line YY’ through
point B2 making an angle α with
XX’.
Y
Y’
α
2. Draw the two toggle positions,
knowing r4 and φ.
B1
B2
φ
3. Calculate the angle α from known
time ratio Q = (180 + α) / (180 – α)

32. Ken Youssefi Mechanical & 32
Synthesis of a Quick – Return Mechanism
O2
X
Y’
O4
X’
Y
B1
B2
7. Locate point C on YY’ so O2C = O2 B1.
C
9. Calculate the length of link 3, AB = r3 = O2 B1 – r2
8. Measure length B2 C, Link 2 = r2 = (B2 C) /2
2r2
A1
r2
A2
A
O4O2
B
10. Verify the motion of the mechanism and check the
minimum transmission angle.