Vibrations from machines mounted on foundations can damage the foundations if not isolated. Devices like springs and dampers can isolate vibrations by absorbing some of the disturbed energy, reducing the amount transmitted to the foundation. The transmissibility ratio describes the ratio of force transmitted to the foundation compared to the force applied to the machine. It depends on factors like the natural frequency of the system and damping. Similarly, the motion transmissibility ratio describes the ratio of amplitudes of the foundation and machine. An example calculates the displacement of a vehicle based on its mass, spring constant, damping, speed, and road surface variation amplitude and wavelength.

1. FORCE TRANSMITTED TO
THE FOUNDATION

2. ISOLATION
Isolation:
When the high speed engines and machines mounted on the
foundations and supports causes vibration of excessive
amplitude because of unbalanced forces set up during their
working. These disturbing forces damage the foundations on
which the machines are mounted.so the vibrations
transmitted to the foundation should be eliminated or
reduced considerably by using some devices such as
springs, dampers, thermo cool sheets etc. between the
foundation and machine. These devices isolate the vibrations
by observing some disturbed energy and allow only a
fraction of it to pass through them to the foundation.

3. TRANSMISSIBILITY
Transmissibility:
It is the ratio of force transverse to the foundation to the
force applied to the machine is known as Transmissibility.
If spring and dampers are used between machine and
foundation then the resultant force transmitted to the
foundation will be vector sum of spring forces and damping
forces.

4. Spring forces = kA
Damping forces= CωA
Ft the resultant force = (𝑘𝐴)2+(𝐶𝜔𝐴)2
= 𝐴 (𝑘)2+(𝐶𝜔)2
Ft = 𝐴𝑘 1 + (
𝐶𝜔
𝑘
)2
Where
𝐶𝜔
𝑘
= 2ξ
𝜔
ωn
Ft = 𝐴𝑘 1 + (2𝜉
𝜔
ωn)2

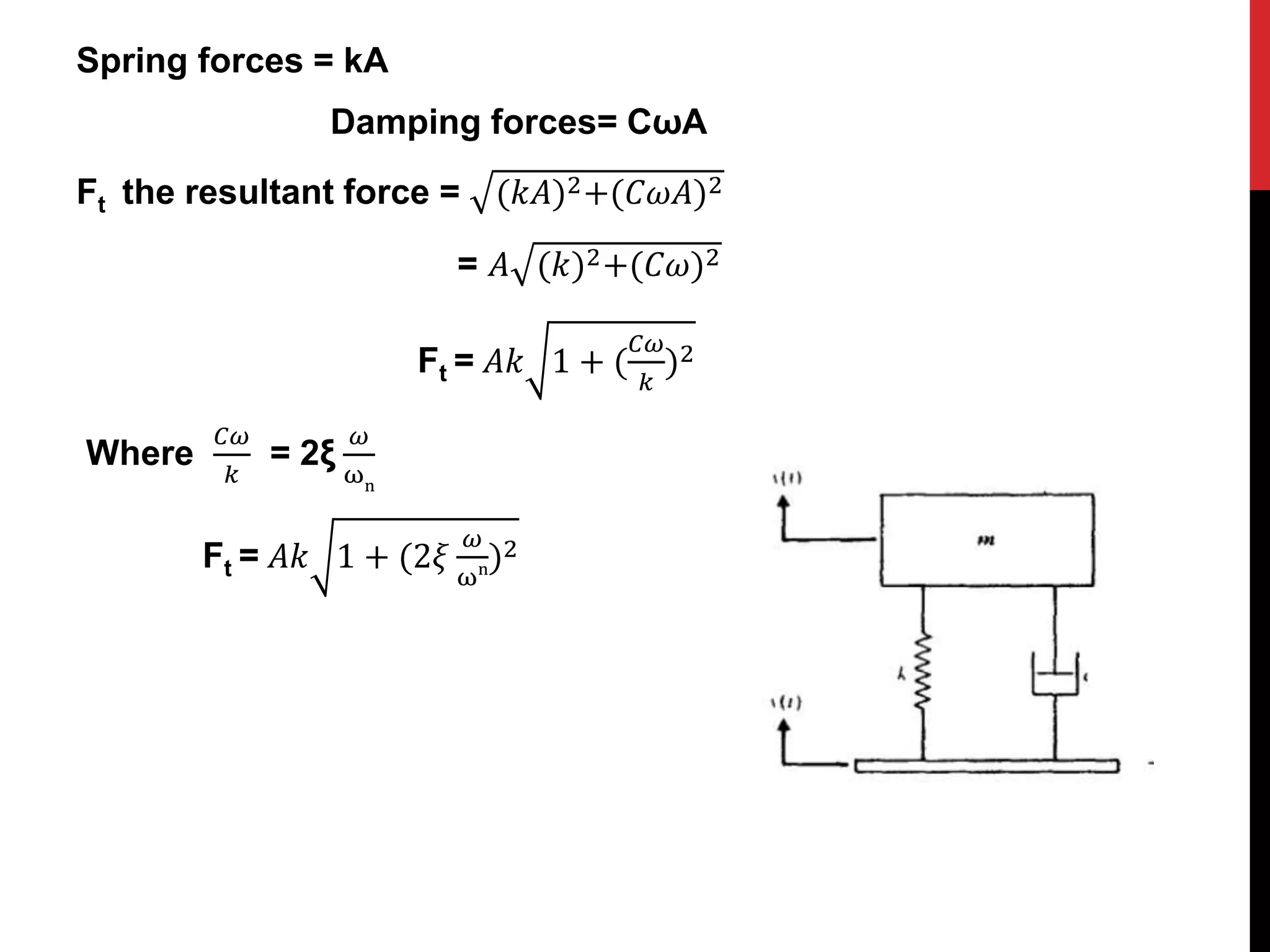
5. The amplitude of forced vibration is
A =
Fo
𝐾
[1−(
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
Fo = 𝐴𝑘 [1 − (
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
Transmissibility ratio T.R =
Ft
Fo
T.R =
𝐴𝑘 1+ 2𝜉
𝜔
ωn
2
𝐴𝑘 [1−(
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
T.R =
1+ 2𝜉
𝜔
ωn
2
[1−(
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
This is the force transmitted to the foundation

6. The motion Transmissibility:
It is the ratio of amplitude of foundation to the amplitude of machine.
When a machine or instrument is to be installed on the platform it under
goes vibration then it is called motion transmissibility.
In case of loco motives vehicles the wheels act as base or support for the
system the wheels can be move vertically up and down on the road surface
during the motion of the vehicle.
Free body diagram:
m𝑥
K(x-y) c(𝑥 − 𝑦)
The equilibrium equation of motion can be written as
𝑚𝑥 + 𝑘(𝑥 − 𝑦) + 𝑐(𝑥 + 𝑦) = 0 ………….. (1)
𝑚𝑥 + 𝑘𝑥 + 𝑐𝑥 = 𝑘𝑦 + 𝑐𝑦 …………..(2)

7. The support is subjected to the harmonic vibration with
amplitude B
𝑦 = 𝐵𝑠𝑖𝑛𝜔𝑡
𝑦 = 𝜔𝐵𝑐𝑜𝑠𝜔𝑡
Put these two equations in equation (2)
𝑚𝑥 + 𝑘𝑥 + 𝑐𝑥 = 𝑘𝐵𝑠𝑖𝑛 𝜔𝑡 + 𝐶𝐵𝑐𝑜𝑠 𝜔𝑡
𝑚𝑥 + 𝑘𝑥 + 𝑐𝑥 = 𝐵(𝑘𝑠𝑖𝑛 𝜔𝑡 + 𝐶𝑐𝑜𝑠 𝜔𝑡)
Multiplying numerator and denominator with 𝑘2 + 𝑐𝜔2
𝑚𝑥 + 𝑘𝑥 + 𝑐𝑥 = 𝐵 𝑘2 + 𝑐𝜔2[
𝑘
𝑘2+𝑐𝜔2 Sin𝜔𝑡 +
𝑐𝜔
𝑘2+𝑐𝜔2
𝑐𝑜𝑠𝜔𝑡]

8. 𝐵 𝑘2 + 𝑐𝜔2
kB 𝑐𝑜𝑠𝛼 =
𝐶𝜔
𝑘2+𝑐𝜔2
CωB 𝑠𝑖𝑛𝛼 =
𝑘
𝑘2+𝑐𝜔2
𝑥 + 𝑘𝑥 + 𝑐𝑥 = 𝐵 𝑘2 + 𝑐𝜔2[𝑆𝑖𝑛𝛼. Sin𝜔𝑡 + 𝑐𝑜𝑠𝛼. 𝑐𝑜𝑠𝜔𝑡]
Assume F = 𝐵 𝑘2 + 𝑐𝜔2
𝑥 + 𝑘𝑥 + 𝑐𝑥 = 𝐹𝑆𝑖𝑛(𝜔𝑡 + 𝛼)
Here amplitude =
𝐹
𝑘

9. A =
F
𝐾
[1−(
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
𝐴 =
𝐵 𝑘2+𝑐𝜔2
𝑘
[1−(
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
𝐴
𝐵
=
1 + 2𝜉
𝜔
ωn
2
[1 − (
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
This is also called as Base excitation equation.

10. A simple example
A simple model of motor vehicle that can be vibrate in
vertical direction while travelling over a rough road the
vehicle has a mass of 1200kg the suspension system has a
spring constant of 400 kN/m and damping factor of 0.5 if the
vehicle speed is 20km/h, determine the displacement of the
vehicle the road surface varies sinusoidal with an amplitude
of 0.05m and a wavelength of 6mts.
Solution:

11. m= 1200kg
k= 400kN/m
ξ= 0.5
v= 20km/h
y=0.05m
λ=6m
𝐴
𝐵
=
1+ 2𝜉
𝜔
ω
n
2
[1−(
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
Natural frequency ωn=
𝑘
𝑚
ωn =
400∗1000
1200

12. ωn =18.257rad/sec
Angular frequency ω = 2πf f =
𝑣
𝜆
ω = 2π
𝑣
𝜆
ω =2*π*
20000
6∗3600
ω=5.18 rad/sec
The amplitude can be found from the equation
𝑥
𝑦
=
1 + 2𝜉
𝜔
ωn
2
[1 − (
𝜔
𝜔𝑛
)2]2+[2𝜉
𝜔
𝜔𝑛
]2
𝑥
𝑦
=
1 + 2 ∗ 0.5 ∗ (
5.817
18.257
)
2
[1 − (
5.817
18.257
)2]2+[2 ∗ 0.5 ∗
5.817
18.257
]2
𝑥
𝑦
= 1.10
𝑥
0.05
= 1.10
𝑥 = 0.07345 𝑚𝑡𝑠

13. THANK YOU