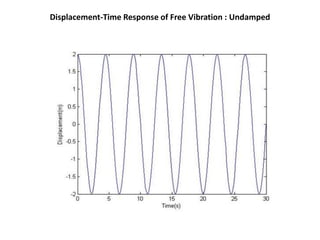
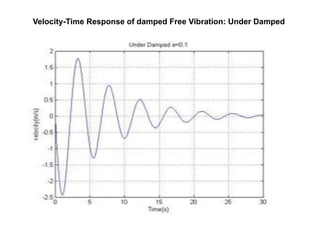
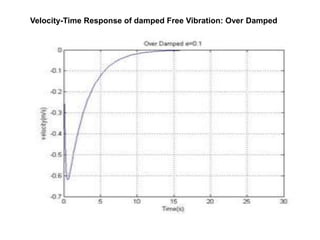
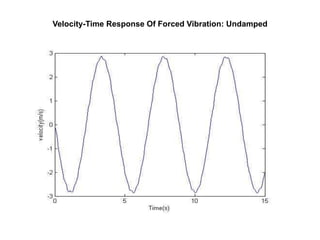
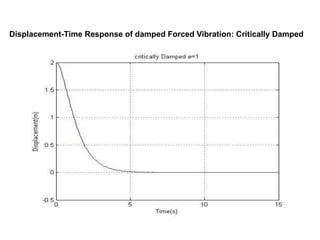
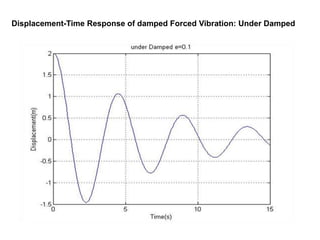
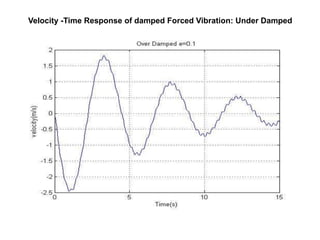
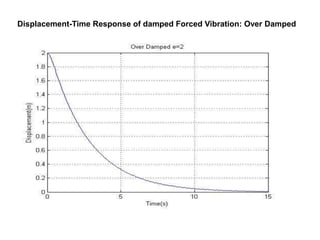
The document presents an analysis of mechanical vibrations in spring mass damper models and machining processes for a Bachelor of Technology thesis in Mechanical Engineering. It discusses types of vibrations, damping influences, and includes experimental results comparing various vibration scenarios and their analysis using MATLAB. Key findings emphasize the significance of vibration monitoring in machining and the use of devices like VibXpert for effective vibration analysis.

1. Analysis of Mechanical Vibration in
spring mass damper model and
Machining Processes
for the partial fulfillment to the degree of Bachelor of Technology
in
Mechanical Engineering
by
Ankur Shukla (2K12/ME/044)
Ankur Gupta (2K12/ME/043)
Aman Handa (2K12/ME/028)
Under the supervision of
Dr. R.C. Singh Shri Rooplal
Mechanical Engineering Department
Delhi Technological University,Delhi-110042

2. INTRODUCTION

3. • Vibration is a mechanical phenomenon
whereby oscillations occur about an
equilibrium point.
• The oscillations may be periodic such as the
motion of a pendulum or random such as the
movement of a tire on a gravel road.
• Vibration is undesirable, wasting energy and
creating unwanted sound – noise.

4. Types of Vibrations
• FREE VIBRATION occurs when a mechanical system is set
off with an initial input and then allowed to vibrate
freely.
• FORCED VIBRATION is when a time-varying disturbance
(load, displacement or velocity) is applied to a
mechanical system. The disturbance can be a periodic,
steady-state input, a transient input, or a random input.

5. DAMPING
• Damping is an influence within or upon an oscillatory system that
has the effect of reducing, restricting or preventing its oscillations.
• OVERDAMPED: The system returns (exponentially decays) to
equilibrium without oscillating.
• CRITICALLY DAMPED: The system returns to equilibrium as quickly
as possible without oscillating.
• UNDERDAMPED: The system oscillates (at reduced frequency
compared to the undamped case) with the amplitude gradually
decreasing to zero.
• UNDAMPED: The system oscillates at its natural resonant frequency
(ωo).

6. SCOPE AND DESCRIPTION OF WORK

7. • In this study we analyzed very basic form of vibrations
such as free, forced vibration with and without damping.
• We have included our experimentation results and these
results are compared with results obtained via MATLAB, to
plot the model natural frequency curve.
• In this study we have represented a vibration analyser,
which is able to analyse the chatter vibration in machining
processes and machine parts and represent it in an easy
and understandable form.
• The objective to conduct this study is to analyse the
different type of vibration in machining processes by
presented vibration analyser.

8. LITERATURE REVIEW

9. • Vibration can be regarded as a branch of dynamics that deals with periodic
and oscillatory motion. Common example of vibration problems are the
response of civil engineering structures to dynamic loading, ambient
condition and earthquakes, vibration of the unbalanced rotating machines
and vibration of power line due to wind excitations, and aircraft wings
[11].
• Vibrations are produced in machine having unbalanced masses. These
vibrations will be transmitted to the foundation upon which the machine
is installed. This is usually undesirable. To diminish the transmitted
vibration, machines are usually mounted on spring or dampers, or on
some other vibration isolating material [12].
• Phani Srikantha A., Woodhouse J. [9] studied parametric identification of
viscous damping models in the context of linear vibration theory.
Frequency domain identification methods based on measured frequency
response functions (FRFs) are considered.

10. •Jiao Chunwang, Liu Jie, Guo Dameng and Wang Qianqian [10] studied that
It is of paramount importance to acquire the response of many nonlinear
forced vibration system. They developed a new method to explore the
approximate analytical solution of forced vibration system which is named
harmonic iteration method (HIM).
•Hao Jiang, Xinhua Long, and Guang Meng [13] said Cutting vibration is
unavoidable during a machining process and has great impact on the
machined surface. With the increase of the demand on the highquality of
surface finish, the effects of cutting vibrationon surface generationattract a
lot of attentions.
•A great deal of research has been carried out on the chatter problem since
the late 1950s, when Tobias and Fishwick [3], Tlusty and Polacek [6] and
Merrit [7] presented the first research results focused on this phenomenon.
Lots of significant advances have been made over the years. Advances in
computers, sensors and actuators have increased understanding of the
phenomena, and developed and improved strategies to solve the problem
[2].

11. NUMERICAL FORMULATION

12. Natural frequency for free vibration without damping
k
m
1
2
푑2푥
푑푡2

13. Natural frequency for free vibration with damping
c
2
m
Time response:

14. FORCED VIBRATION WITHOUT DAMPING

15. Forced Vibration with damping

16. Two Degrees of Freedom: Vibration
Equations of Motion:
Using matrix notation:

17. Definition of matrices:
Mass Matrix (M):
Stiffness Matrix (k):
General Equation:
General Solution:

18. Two Degree of Freedom: Vibration
with damping
Equations of motion:
This can be rewritten in matrix format:

19. More compact form:
This differential equation can be solved by assuming the following type of
solution:
Now equation becomes an eigen value problem
The solution to the problem results in N eigenvalues (i.e. ), where N
corresponds to the number of degrees of freedom.
Note: This method can applied for multiple degree of vibration.

20. MODELLING

21. Simscape Model

22. Simulink Model

23. MATLAB : Time Response For
Different Types of Vibration

24. Displacement-Time Response of Free Vibration : Undamped

25. Velocity-Time Responce of Free Vibration: Undamped

26. Displacement-Time Responce of damped Free Vibration: Critically Damped

27. Velocity-Time Responce of damped Free Vibration: Critically Damped

28. Displacement-Time Responce of damped Free Vibration: Under Damped

29. Velocity-Time Response of damped Free Vibration: Under Damped

30. Displacement-Time Response of damped Free Vibration: Over Damped

31. Velocity-Time Response of damped Free Vibration: Over Damped

32. Displacement-Time Response of Forced Vibration: Undamped

33. Velocity-Time Response Of Forced Vibration: Undamped

34. Displacement-Time Response of damped Forced Vibration: Critically Damped

35. Velocity-Time Response of damped Forced Vibration: Critically Damped

36. Displacement-Time Response of damped Forced Vibration: Under Damped

37. Velocity -Time Response of damped Forced Vibration: Under Damped

38. Displacement-Time Response of damped Forced Vibration: Over Damped

39. Velocity -Time Response of damped Forced Vibration: Over Damped

40. VIBRATION ANALYSIS

41. • The frequency analysis involves a frequency spectrum which
provides us with the detailed information of the signal sources not able
to be obtained from the time signal.
• It provides information on the vibrations caused due to rotating
parts and tooth meshing.
• Process involves sending a signal through a filter and at the same
time sweeping the filter over the frequency range of filters, it gives us
the frequency spectrum.
• Monitoring of a fan: The most likely fault to occur is unbalance, This
will normally also be the highest level in the spectrum. To see if
unbalance is developing, it is therefore sufficient to measure the
overall level at regular intervals

42. • The overall level will reflect the increase just as well as the
spectrum.
• Monitoring of a gearbox: Damaged or worn gears will show up as
an increase in the vibration level at the tooth meshing frequencies
(shaft RPM number of teeth) and their harmonics.
• The levels at these frequencies are normally much lower than the
highest level in the frequency spectrum, so it is necessary to use a
full spectrum comparison to reveal a developing fault.
• Presenting the data: The data is presented in the form of linear
scales with ranges dictated by the range of data but it does not
allow to see some important data ,Hence logarithmic scales are
used.

43. VIBXPERT
• VIBXPERT is a device that helps in vibrations analysis. It provides us
with many key functions.
• Route based data collection ,Vibration diagnosis ,Field balancing ,
Multimeter ,Data logging ,Visual inspection ,Print reports on USB
stick ,Time waveform ,Amplitude spectrum , Static shaft position
(for balancing) ,Long term recording ,Printing of measurement
reports are the functions it performs

44. Refrences

45. Bibliography
[1]. Tobias, S.A. Machine Tool Vibration. Spain : UMRO, 1961.
[2]. Chatter in machining process: A review. Guillem Quintana, Joquim Ciurana. 2011, International Journal of
Machine tools and Manufacture, pp. 363-376.
[3]. S.A. Tobais, W. Fishwick. Theory of regenerative machine tool chatter. s.l. : The Engineer, 1958.
[4]. A review of chatter vibration research in turning. M. Siddhpura, R. Paurobally. 1, s.l. : ELSEVIER, 2012,
International Journal of machine tools and manufacture, Vol. 61, pp. 27-47.
[5]. On the art of cutting metals. F.Taylor. 1907, Transactions of ASME , Vol. 28.
[6]. The stability of machine tools against self-excited vibrations in machining. J. Tlusty, M. Polacek. 1963,
International Research in Production Engineering, pp. 465–474.
[7]. Theory of self-excited machine-tool chatter-contribution to machine tool chatter research—1. Merrit, H.E.
1965, ASME Journal of Engineering for Industry, pp. 447-454.
[8]. Robust Analysis of Stability in Internal Turning. Giovanni Totis, Marco Sortino. Udine, Italy : ELSEVIER, 2014.
24th DAAAM International Symposium on Intelligent Manufacturing and Automation. Vol. 69, pp. 1306-1315.
[9]. Viscous damping identification in linear vibration. S. Adhikari, J. Woodhouse. 2007, Journal of Sound and
Vibration , Vol. 303, pp. 475-500.
[10]. Jiao Chunwang, Liu Jie, Guo Dameng and Wang Qianqian. A New Method for Solving Nonlinear Forced
Vibration System Response. 2010.
[11]. Wahab, M. A. Dynamics and Vibration: An Introduction. s.l. : John Wiley & Sons Ltd., 2008.
[12]. Rattan, S.S. Theory of Machines. 3. New Delhi : McGraw Hill Education (India) Private Ltd., 2009.
[13]. Study of the correlation between surface generation and cutting vibrations in peripheral milling. Hao
Jiang, Xinhua Long, Guang Meng. Shanghai, China : s.n., 2008, journal of materials processing technology, Vol.
208, pp. 229-238.