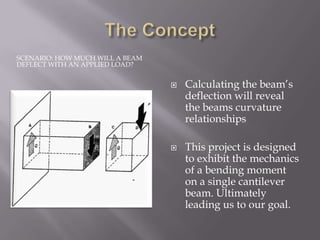
The document outlines an experiment to investigate how aluminum and brass beams deflect under various applied loads, utilizing a cantilever beam setup. The goals include calculating Young’s modulus based on measured deflections and comparing it with tabulated values, with results indicating higher than expected deflections and an error margin of 10-20%. The structure and analysis, including MATLAB code for deflection calculations, are detailed alongside initial results and conclusions regarding the mechanical properties of the materials tested.

1. Mechanics of Materials: Beam DeflectionsEngineered by Group 20 Christopher Webb, Anthony Williams, Carlaton Wong, Jonathan Wong03/03/2010

2. The ConceptScenario: How much will a beam deflect with an applied load?Calculating the beam’s deflection will reveal the beams curvature relationshipsThis project is designed to exhibit the mechanics of a bending moment on a single cantilever beam. Ultimately leading us to our goal.

3. Goals & ObjectivesExperimental GoalsHow much will aluminum and brass deflect with various applied loads?Determine the Young’s Modulus based on the deflection measuredDoes our calculated Young’s Modulus equal tabulated values?

4. Beam Failures

5. What is Beam Deflection?When loads are applied to a beam, the beam’s axis that was once straight will become curved. The displacements from the initial axis are called bending or flexural deflections.

6. Apparatus Design & OperationThe beam in use will be fixed onto the standing wooden plank by securing it at the top of the apparatus with a c-clamp.

7. At the end of the beam there will be an attachment to serve as the applied load.

8. This experiment used strategically filled water bottles for the applied loads.Apparatus Design & Operation (cont.)The deflection of the beam by the applied load can be recorded at the point of loading.

9. Cantilever beams are interchangeable allowing for supplemental testing of differing materials & structural make-ups .

10. Negligible factors:

11. Load’s tiny distance from free end of member

12. Small bend in beam after multiple loadsCost Factors Involved

13. Our Cantilever Beam

14. Superposition Table

15. MatLab Codehold on; grid onplot(x/in_m,v2*100,'g-*',x/in_m,v1*100,'ro-',x/in_m,v1*100+v2*100,'b*-')title('Beam Deflection of Brass w/ 0.3lb Load')xlabel('Beam Length (in)')ylabel('Deflection (cm)')legend('DistributedLoad','ConcentratedLoad','Total Deflection',3)V_max=(q*L+F)/(b*h);%Max shear stresssigma_max=(.5*q*L^2+F*L)*(h*0.5)/I;v_max_tot=(v1(end)+v2(end))*100; %Analysis of Aluminum Beamclose all;clearall;clc%Conversion Factorsin_m=0.0254; %inch to meter lb_N=0.22481;%Pound force to Newton %Material PropertiesE=69*10^9;%Pa Aluminum%Geometric Properties(in SI units)%Al bar datah=(1/8)*in_m;%Cross section heightb=(3/4)*in_m;%Cross sect widthL=15*in_m;%Length of Beam (m)I=(b*h^3)/12; %second momemnt of inertia(m^4)%Analysis of Brass beamclose all;clearall;clc%Conversion Factorsin_m=0.0254; %inch to meter lb_N=0.22481;%Pound force to Newton %Material PropertiesE=100*10^9;%Pa Brass%Geometric Properties(in SI units)%Brass Bar datah=(.064)*in_m;%Cross section heightb=(3/4)*in_m;%Cross sect widthL=9*in_m;%Length of Beam (m)I=(b*h^3)/12; %second momemnt of inertia(m^4)%Applied forceF=(.3)/lb_N; %(N)%Calculating deflectionx=linspace(0,L,50);v1=(F*x.^3/6 - F*L*x.^2/2)/(E*I);%Deflection due to concentrated loadq=79.7*10^-3*9.81/(12*.0254);v2=zeros(1,length(x));for i=1:length(x)v2(i)=-q*x(i)^2/(24*E*I)*(6*L^2-4*L*x(i) + x(i)^2);%Deflection due to weight of barend%Applied forceF=(.3)/lb_N;%Calculating deflection %Concetrated loadx=linspace(0,L,50); v1=(F*x.^3/6 - F*L*x.^2/2)/(E*I);%Deflection in (m) %Distributed weightq=74*10^-3*9.81/(18.5*.0254); v2=zeros(1,length(x)); for i=1:length(x) v2(i)=-q*x(i)^2/(24*E*I)*(6*L^2-4*L*x(i) + x(i)^2); endhold on;grid on; plot(x/in_m,v1*100,'ro',x/in_m,v2*100,'g*',x/in_m,v1*100+v2*100,'b*')title('Beam Deflection of Aluminum w/ 0.3lb Load')xlabel('Beam Length (in)')ylabel('Deflection (cm)')legend('DistributedLoad','ConcentratedLoad','Total Deflection',3)V_max=(q*L+F)/(b*h)%Max shear stresssigma_max=(.5*q*L^2+F*L)*(h*0.5)/I;v_max_tot=(v1(end)+v2(end))*100;

17. Experiment Variables Second Moment of Inertia (I) determined by measuring geometry of the beams.

18. Calculated Linear Weight Density by weighing the beams on a scale.

19. Water bottles with a known mass used to calculate forces applied to the beam.Results – Initial Height

20. Results – Brass Bar.3 Lbs Force.4 Lbs Force.5 Lbs Force

21. Results – Aluminum Bar.3 Lbs Force.4 Lbs Force.5 Lbs Force

22. Experimental ResultsAluminum :Expected Young’s Modulus:69 GPaBrass:Expected Young’s Modulus:100 GPa