Downloaded 67 times
Uploaded byClearCalcs
Worked Examples for Timber Beam Design to AS1720.1 Webinar
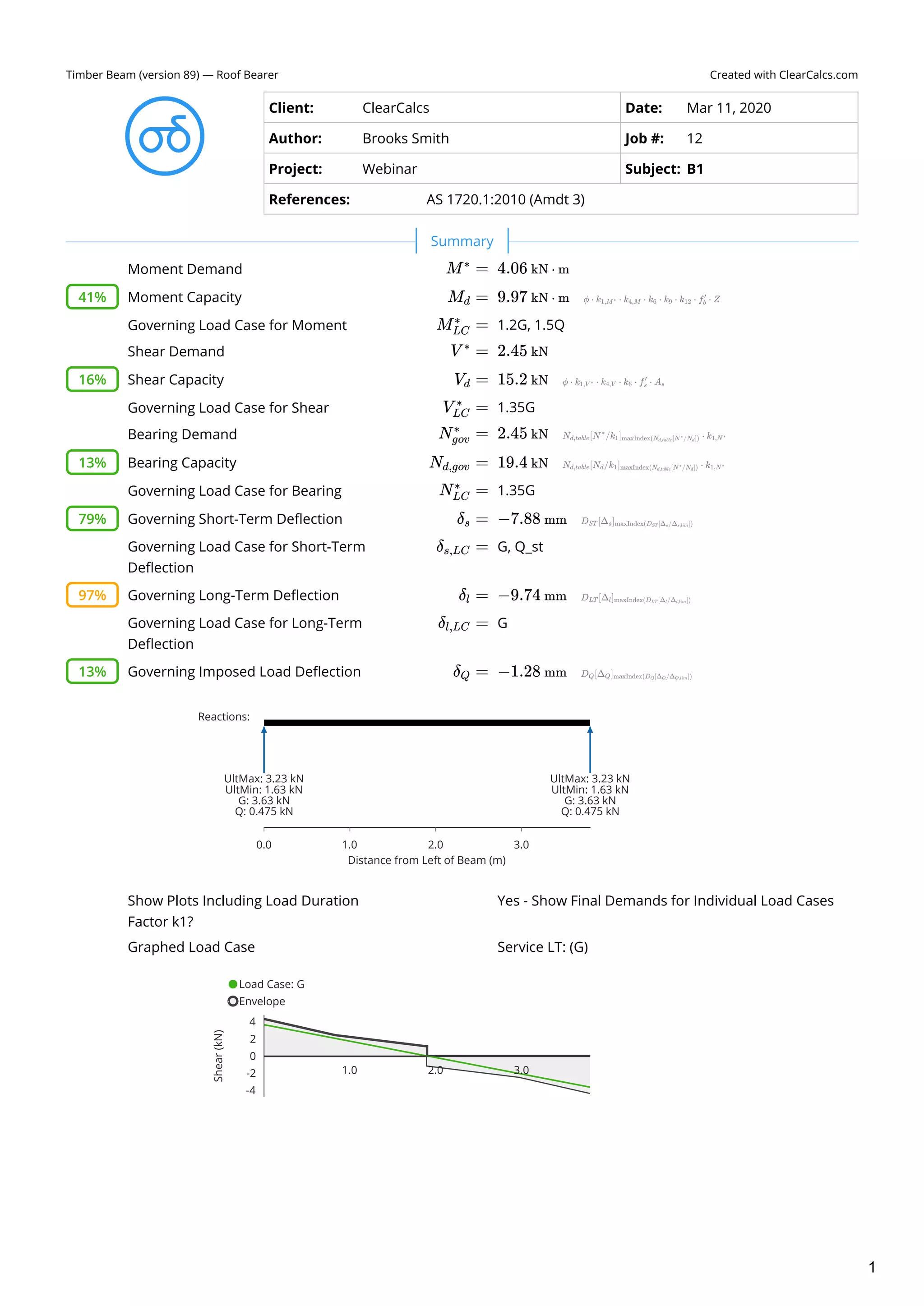
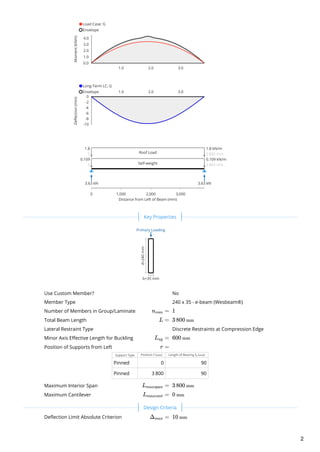
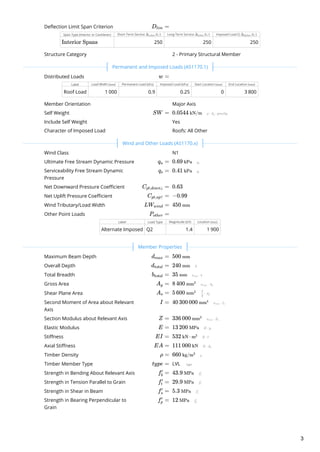
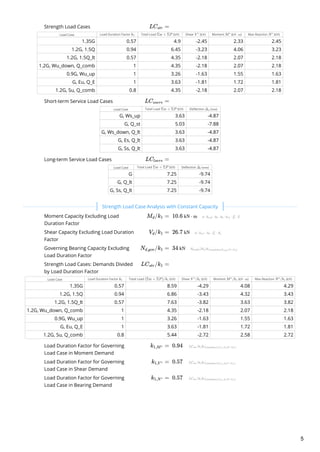
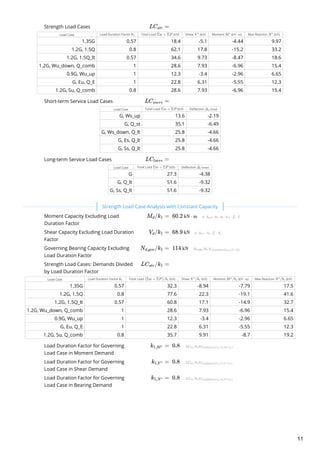
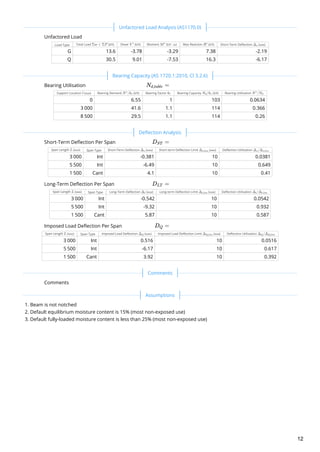
This document analyzes a timber beam used as a floor bearer. It summarizes the demands on the beam from different load cases, including moment, shear, bearing and deflection. The governing load cases are identified as 1.2G, 1.5Q for moment, shear and bearing demands. Short-term deflection is governed by load case G, Q_st, while long-term deflection is governed by G, Q_lt. The beam properties, load cases, demands and capacities are analyzed according to AS1720.1:2010 timber design standard.
More Related Content
Similar to Worked Examples for Timber Beam Design to AS1720.1 Webinar
Worked Examples for Timber Beam Design to AS1720.1 Webinar
- 1. Created with ClearCalcs.comTimberBeam (version 89) — Roof Bearer Client: ClearCalcs Date: Mar 11, 2020 Author: Brooks Smith Job #: 12 Project: Webinar Subject: B1 References: AS 1720.1:2010 (Amdt 3) Moment Demand Moment Capacity Governing Load Case for Moment 1.2G, 1.5Q Shear Demand Shear Capacity Governing Load Case for Shear 1.35G Bearing Demand Bearing Capacity Governing Load Case for Bearing 1.35G Governing Short-Term Deflection Governing Load Case for Short-Term Deflection G, Q_st Governing Long-Term Deflection Governing Load Case for Long-Term Deflection G Governing Imposed Load Deflection Show Plots Including Load Duration Factor k1? Graphed Load Case M =∗ 4.06 kN ⋅ m 41% M =d 9.97 kN ⋅ m M =LC ∗ V =∗ 2.45 kN 16% V =d 15.2 kN V =LC ∗ N =gov ∗ 2.45 kN 13% N =d,gov 19.4 kN N =LC ∗ 79% δ =s −7.88 mm δ =s,LC 97% δ =l −9.74 mm δ =l,LC 13% δ =Q −1.28 mm Reactions: Distance from Left of Beam (m) 0.0 1.0 2.0 3.0 UltMax: 3.23 kN UltMin: 1.63 kN G: 3.63 kN Q: 0.475 kN UltMax: 3.23 kN UltMin: 1.63 kN G: 3.63 kN Q: 0.475 kN Yes - Show Final Demands for Individual Load Cases Service LT: (G) Load Case: G Envelope 1.0 2.0 3.0 Shear(kN) -4 -2 0 2 4 Summary 1
- 2. Use Custom Member? MemberType Number of Members in Group/Laminate Total Beam Length Lateral Restraint Type Minor Axis Effective Length for Buckling Position of Supports from Left Support Type Position ( ) Length of Bearing ( ) Pinned 0 90 Pinned 3 800 90 Maximum Interior Span Maximum Cantilever Deflection Limit Absolute Criterion Load Case: G Envelope 1.0 2.0 3.0 Moment(kNm) 0.0 1.0 2.0 3.0 4.0 Long-Term LC: G Envelope 1.0 2.0 3.0 Deflection(mm) -10 -8 -6 -4 -2 0 Distance from Left of Beam (mm) 0 1,000 2,000 3,000 Self-weight 0.109 0 3 800 mm 0.109 kN/m Roof Load 1.8 0 3 800 mm 1.8 kN/m 3.63 kN 3.63 kN d=240mm b=35 mm Primary Loading No 240 x 35 - e-beam (Wesbeam®) n =com 1 L = 3 800 mm Discrete Restraints at Compression Edge L =ay 600 mm r = l mm l b mm L =maxspan 3 800 mm L =maxcant 0 mm Δ =max 10 mm Key Properties Design Criteria 2
- 3. Deflection Limit SpanCriterion Span Type (Interior or Cantilever) Short-Term Service ( ) Long-Term Service ( ) Imposed Load Q ( ) 250 250 250 Structure Category Distributed Loads Label Load Width ( ) Permanent Load ( ) Imposed Load ( ) Start Location ( ) End Location ( ) Roof Load 1 000 0.9 0.25 0 3 800 Member Orientation Self Weight Include Self Weight Character of Imposed Load Wind Class Ultimate Free Stream Dynamic Pressure Serviceability Free Stream Dynamic Pressure Net Downward Pressure Coefficient Net Uplift Pressure Coefficient Wind Tributary/Load Width Other Point Loads Label Load Type Magnitude ( ) Location ( ) Alternate Imposed Q2 1.4 1 900 Maximum Beam Depth Overall Depth Total Breadth Gross Area Shear Plane Area Second Moment of Area about Relevant Axis Section Modulus about Relevant Axis Elastic Modulus Stiffness Axial Stiffness Timber Density Timber Member Type LVL Strength in Bending About Relevant Axis Strength in Tension Parallel to Grain Strength in Shear in Beam Strength in Bearing Perpendicular to Grain D =lim Δ s,lim L/ Δ l,lim L/ Δ Q,lim L/ Interior Spans 2 - Primary Structural Member w = mm kPa kPa mm mm Major Axis SW = 0.0544 kN/m Yes Roofs: All Other N1 q =u 0.69 kPa q =s 0.41 kPa C =pt,down↓ 0.63 C =pt,up↑ −0.99 LW =wind 450 mm P =other kN mm d =max 500 mm d =total 240 mm b =total 35 mm A =g 8 400 mm2 A =s 5 600 mm2 I = 40 300 000 mm4 Z = 336 000 mm3 E = 13 200 MPa EI = 532 kN ⋅ m2 EA = 111 000 kN ρ = 660 kg/m3 type = f =b ′ 43.9 MPa f =t ′ 29.9 MPa f =s ′ 5.3 MPa f =p ′ 12 MPa Permanent and Imposed Loads (AS1170.1) Wind and Other Loads (AS1170.x) Member Properties 3
- 4. Capacity Factor InitialMoisture Content Seasoned Initial Moisture Content from Member Selection Equilibrium Moisture Content (Annual Average) Partial Seasoning Factor for Bending Partial Seasoning Factor for Shear Partial Seasoning Factor for Modulus of Elasticity Temperature Factor Number of Discrete Parallel Members Geometric Factor in a Combined Parallel System Geometric Factor in a Discrete System Strength Sharing Factor Slenderness Coefficient Design Action Ratio Material Constant in Beams Stability Factor Creep Factor Table Long-Duration Creep ≤1 day 1 week 1 month 3 months ≥1 year 1 1.33 1.58 1.76 2 0.5 0.665 0.788 0.881 1 Creep Factor for Permanent and Long- Term Imposed Loads Load Duration Factors Load Duration: 5 seconds 5 minutes 5 hours 5 days 5 months 50+ years Variable (5d - 5mo) 1 1 0.97 0.94 0.8 0.57 0.94 1 1 1.03 1.06 1.25 1.75 1.06 Character of Imposed Load Factors Imposed Load Type Short-Term Factor Long-Term Factor Combination Factor Earthquake Factor 0.7 0 0 0 1 0 0 0 ϕ = 0.9 mc = IMC = 15 % EMC = 15 % k =4,M 1 k =4,V 1 j =6 1 k =6 1 1 or 2 g =31 1 g =32 1 k =9 1 S =1 13.6 r =ub 0.25 ρ =b 1.03 k =12 0.799 j =2,table Factor: j 2 Fraction of max: j /j 2 2,max j =2,max 2 k =1,table Factor: k 1 Inverse: 1/k 1 CharQ = Ψ s ψ l Ψ c Ψ E Distributed Concentrated Modification Factors (AS1720.1, Cl 2.4) Load Case Analysis (AS1170.0) 4
- 5. Strength Load Cases LoadCase Load Duration Factor Total Load ( ) Shear ( ) Moment ( ) Max Reaction ( ) 1.35G 0.57 4.9 -2.45 2.33 2.45 1.2G, 1.5Q 0.94 6.45 -3.23 4.06 3.23 1.2G, 1.5Q_lt 0.57 4.35 -2.18 2.07 2.18 1.2G, Wu_down, Q_comb 1 4.35 -2.18 2.07 2.18 0.9G, Wu_up 1 3.26 -1.63 1.55 1.63 G, Eu, Q_E 1 3.63 -1.81 1.72 1.81 1.2G, Su, Q_comb 0.8 4.35 -2.18 2.07 2.18 Short-term Service Load Cases Load Case Total Load ( ) Deflection ( ) G, Ws_up 3.63 -4.87 G, Q_st 5.03 -7.88 G, Ws_down, Q_lt 3.63 -4.87 G, Es, Q_lt 3.63 -4.87 G, Ss, Q_lt 3.63 -4.87 Long-term Service Load Cases Load Case Total Load ( ) Deflection ( ) G 7.25 -9.74 G, Q_lt 7.25 -9.74 G, Ss, Q_lt 7.25 -9.74 Moment Capacity Excluding Load Duration Factor Shear Capacity Excluding Load Duration Factor Governing Bearing Capacity Excluding Load Duration Factor Strength Load Cases: Demands Divided by Load Duration Factor Load Case Load Duration Factor Total Load ( ) Shear ( ) Moment ( ) Max Reaction ( ) 1.35G 0.57 8.59 -4.29 4.08 4.29 1.2G, 1.5Q 0.94 6.86 -3.43 4.32 3.43 1.2G, 1.5Q_lt 0.57 7.63 -3.82 3.63 3.82 1.2G, Wu_down, Q_comb 1 4.35 -2.18 2.07 2.18 0.9G, Wu_up 1 3.26 -1.63 1.55 1.63 G, Eu, Q_E 1 3.63 -1.81 1.72 1.81 1.2G, Su, Q_comb 0.8 5.44 -2.72 2.58 2.72 Load Duration Factor for Governing Load Case in Moment Demand Load Duration Factor for Governing Load Case in Shear Demand Load Duration Factor for Governing Load Case in Bearing Demand LC =str k 1 Σw + ΣP kN V ∗ kN M∗ kN ⋅ m N∗ kN LC =sserv Σw + ΣP kN Δ s mm LC =lserv Σw + ΣP kN Δ l mm M /k =d 1 10.6 kN ⋅ m V /k =d 1 26.7 kN N /k =d,gov 1 34 kN LC /k =str 1 k 1 (Σw + ΣP)/k 1 kN V /k ∗ 1 kN M /k ∗ 1 kN ⋅ m N /k ∗ 1 kN k =1,M∗ 0.94 k =1,V ∗ 0.57 k =1,N∗ 0.57 Strength Load Case Analysis with Constant Capacity 5
- 6. Unfactored Load Load TypeTotal Load ( ) Shear ( ) Moment ( ) Max Reaction ( ) Short-Term Deflection ( ) G 3.63 -1.81 1.72 1.81 -4.87 Q 0.95 -0.475 0.451 0.475 -1.28 Bearing Utilisation Support Location ( ) Bearing Demand ( ) Bearing Factor Bearing Capacity ( ) Bearing Utilisation 0 4.29 1 34 0.126 3 800 4.29 1 34 0.126 Short-Term Deflection Per Span Span Length ( ) Span Type Short-Term Deflection ( ) Short-term Deflection Limit ( ) Deflection Utilisation 3 800 Int -7.88 10 0.788 Long-Term Deflection Per Span Span Length ( ) Span Type Long-Term Deflection ( ) Long-term Deflection Limit ( ) Deflection Utilisation 3 800 Int -9.74 10 0.974 Imposed Load Deflection Per Span Span Length ( ) Span Type Imposed Load Deflection ( ) Imposed Load Deflection Limit ( ) Deflection Utilisation 3 800 Int -1.28 10 0.128 Comments Beam is not notched Default equilibrium moisture content is 15% (most non-exposed use) Default fully-loaded moisture content is less than 25% (most non-exposed use) Σw + ΣP kN V ∗ kN M∗ kN ⋅ m R∗ kN Δ s mm N =d,table l mm N /k ∗ 1 kN k 7 N /k d 1 kN N /N ∗ d D =ST L mm Δ s mm Δ s,lim mm Δ /Δ s s,lim D =LT L mm Δ l mm Δ l,lim mm Δ /Δ l l,lim D =Q L mm Δ Q mm Δ Q,lim mm Δ /Δ Q Q,lim 1. 2. 3. Unfactored Load Analysis (AS1170.0) Bearing Capacity (AS 1720.1:2010, Cl 3.2.6) Deflection Analysis Comments Assumptions 6
- 7. Created with ClearCalcs.comTimberBeam (version 89) — Floor Bearer Client: ClearCalcs Date: Mar 11, 2020 Author: Brooks Smith Job #: 12 Project: Webinar Subject: B2 References: AS 1720.1:2010 (Amdt 3) Moment Demand Moment Capacity Governing Load Case for Moment 1.2G, 1.5Q Shear Demand Shear Capacity Governing Load Case for Shear 1.2G, 1.5Q Bearing Demand Bearing Capacity Governing Load Case for Bearing 1.2G, 1.5Q Governing Short-Term Deflection Governing Load Case for Short-Term Deflection G, Q_st Governing Long-Term Deflection Governing Load Case for Long-Term Deflection G, Q_lt Governing Imposed Load Deflection Show Plots Including Load Duration Factor k1? Graphed Load Case M =∗ −15.2 kN ⋅ m 32% M =d 48.2 kN ⋅ m M =LC ∗ V =∗ 17.8 kN 32% V =d 55.1 kN V =LC ∗ N =gov ∗ 33.2 kN 37% N =d,gov 90.9 kN N =LC ∗ 65% δ =s −6.49 mm δ =s,LC 93% δ =l −9.32 mm δ =l,LC 62% δ =Q −6.17 mm Reactions: Distance from Left of Beam (m) 0 2 4 6 8 10 UltMax: 5.24 kN UltMin: 1.42 kN G: 3.17 kN Q: 2.23 kN UltMax: 33.2 kN UltMin: 6.65 kN G: 14.8 kN Q: 16.3 kN UltMax: 23.6 kN UltMin: 4.2 kN G: 9.33 kN Q: 12 kN No - Show Envelope Plots Divided by k1 Strength: (1.2G, 1.5Q) Load Case: 1.2G, 1.5Q Envelope 2 4 6 8 10 Shear(kN) -20 -10 0 10 20 Summary 7
- 8. Use Custom Member? TimberGrade Timber Species Depth of Custom Section Breadth of Single Member/Laminate in Custom Member Number of Members in Group/Laminate Total Beam Length Lateral Restraint Type Minor Axis Effective Length for Buckling Position of Supports from Left Support Type Position ( ) Length of Bearing ( ) Pinned 0 90 Pinned 3 000 90 Pinned 8 500 90 Maximum Interior Span Maximum Cantilever Deflection Limit Absolute Criterion Load Case: 1.2G, 1.5Q Envelope 2 4 6 8 10 Moment(kNm) -20 -10 0 10 Distance from Left of Beam (mm) 0 2,000 4,000 6,000 8,000 10,000 Self-weight 0.273 0 10 000 mm 0.273 kN/m Floor Load 7.13 0 10 000 mm 7.13 kN/m B1-2 3.61 kN Alternate Imposed 3.38 kN 6.55 kN 41.6 kN 29.5 kN width=135 mm height=250mm Primary Loading Yes F17 Pine, Radiata (Australia & New Zealand, heart-in material included) - Seasoned d = 250 mm b = 45 mm n =com 3 L = 10 000 mm Discrete Restraints at Compression Edge L =ay 450 mm r = l mm l b mm L =maxspan 5 500 mm L =maxcant 1 500 mm Δ =max 10 mm Key Properties Design Criteria 8
- 9. Deflection Limit SpanCriterion Span Type (Interior or Cantilever) Short-Term Service ( ) Long-Term Service ( ) Imposed Load Q ( ) 300 300 300 150 150 150 Structure Category Distributed Loads Label Load Width ( ) Permanent Load ( ) Imposed Load ( ) Start Location ( ) End Location ( ) Floor Load 2 000 0.5 1.5 0 10 000 Point Loads Label Permanent Load ( ) Imposed Load ( ) Location ( ) B1-2 1.81 0.475 1 500 Member Orientation Self Weight Include Self Weight Character of Imposed Load Wind Class Ultimate Free Stream Dynamic Pressure Serviceability Free Stream Dynamic Pressure Net Downward Pressure Coefficient Net Uplift Pressure Coefficient Wind Tributary/Load Width Other Point Loads Label Load Type Magnitude ( ) Location ( ) Alternate Imposed Q2 1.8 10 000 Maximum Beam Depth Overall Depth Total Breadth Gross Area Shear Plane Area Second Moment of Area about Relevant Axis Section Modulus about Relevant Axis Elastic Modulus Stiffness Axial Stiffness Timber Density Timber Member Type Sawn High Grade Strength in Bending About Relevant Axis Strength in Tension Parallel to Grain D =lim Δ s,lim L/ Δ l,lim L/ Δ Q,lim L/ Interior Spans Cantilevers 2 - Primary Structural Member w = mm kPa kPa mm mm P = kN kN mm Major Axis SW = 0.182 kN/m Yes Floors: Residential and Domestic N1 q =u 0.69 kPa q =s 0.41 kPa C =pt,down↓ 0 C =pt,up↑ 0 LW =wind 450 mm P =other kN mm d =max 500 mm d =total 250 mm b =total 135 mm A =g 33 800 mm2 A =s 22 500 mm2 I = 176 000 000 mm4 Z = 1 410 000 mm3 E = 14 000 MPa EI = 2 460 kN ⋅ m2 EA = 473 000 kN ρ = 550 kg/m3 type = f =b ′ 42 MPa f =t ′ 22 MPa Permanent and Imposed Loads (AS1170.1) Wind and Other Loads (AS1170.x) Member Properties 9
- 10. Strength in Shearin Beam Strength in Bearing Perpendicular to Grain Capacity Factor Initial Moisture Content Seasoned Initial Moisture Content from Member Selection Equilibrium Moisture Content (Annual Average) Partial Seasoning Factor for Bending Partial Seasoning Factor for Shear Partial Seasoning Factor for Modulus of Elasticity Temperature Factor Number of Discrete Parallel Members Geometric Factor in a Combined Parallel System Geometric Factor in a Discrete System Strength Sharing Factor Slenderness Coefficient Design Action Ratio Material Constant in Beams Stability Factor Creep Factor Table Long-Duration Creep ≤1 day 1 week 1 month 3 months ≥1 year 1 1.33 1.58 1.76 2 0.5 0.665 0.788 0.881 1 Creep Factor for Permanent and Long- Term Imposed Loads Load Duration Factors Load Duration: 5 seconds 5 minutes 5 hours 5 days 5 months 50+ years Variable (5d - 5mo) 1 1 0.97 0.94 0.8 0.57 0.8 1 1 1.03 1.06 1.25 1.75 1.25 Character of Imposed Load Factors Imposed Load Type Short-Term Factor Long-Term Factor Combination Factor Earthquake Factor 0.7 0.4 0.4 0.3 1 0.4 0.4 0.3 f =s ′ 3.6 MPa f =p ′ 10 MPa ϕ = 0.85 mc = IMC = 15 % EMC = 15 % k =4,M 1 k =4,V 1 j =6 1 k =6 1 1 or 2 g =31 1.2 g =32 1.2 k =9 1.2 S =1 3.11 r =ub 0.25 ρ =b 0.985 k =12 1 j =2,table Factor: j 2 Fraction of max: j /j 2 2,max j =2,max 2 k =1,table Factor: k 1 Inverse: 1/k 1 CharQ = Ψ s ψ l Ψ c Ψ E Distributed Concentrated Modification Factors (AS1720.1, Cl 2.4) Load Case Analysis (AS1170.0) 10
- 11. Strength Load Cases LoadCase Load Duration Factor Total Load ( ) Shear ( ) Moment ( ) Max Reaction ( ) 1.35G 0.57 18.4 -5.1 -4.44 9.97 1.2G, 1.5Q 0.8 62.1 17.8 -15.2 33.2 1.2G, 1.5Q_lt 0.57 34.6 9.73 -8.47 18.6 1.2G, Wu_down, Q_comb 1 28.6 7.93 -6.96 15.4 0.9G, Wu_up 1 12.3 -3.4 -2.96 6.65 G, Eu, Q_E 1 22.8 6.31 -5.55 12.3 1.2G, Su, Q_comb 0.8 28.6 7.93 -6.96 15.4 Short-term Service Load Cases Load Case Total Load ( ) Deflection ( ) G, Ws_up 13.6 -2.19 G, Q_st 35.1 -6.49 G, Ws_down, Q_lt 25.8 -4.66 G, Es, Q_lt 25.8 -4.66 G, Ss, Q_lt 25.8 -4.66 Long-term Service Load Cases Load Case Total Load ( ) Deflection ( ) G 27.3 -4.38 G, Q_lt 51.6 -9.32 G, Ss, Q_lt 51.6 -9.32 Moment Capacity Excluding Load Duration Factor Shear Capacity Excluding Load Duration Factor Governing Bearing Capacity Excluding Load Duration Factor Strength Load Cases: Demands Divided by Load Duration Factor Load Case Load Duration Factor Total Load ( ) Shear ( ) Moment ( ) Max Reaction ( ) 1.35G 0.57 32.3 -8.94 -7.79 17.5 1.2G, 1.5Q 0.8 77.6 22.3 -19.1 41.6 1.2G, 1.5Q_lt 0.57 60.8 17.1 -14.9 32.7 1.2G, Wu_down, Q_comb 1 28.6 7.93 -6.96 15.4 0.9G, Wu_up 1 12.3 -3.4 -2.96 6.65 G, Eu, Q_E 1 22.8 6.31 -5.55 12.3 1.2G, Su, Q_comb 0.8 35.7 9.91 -8.7 19.2 Load Duration Factor for Governing Load Case in Moment Demand Load Duration Factor for Governing Load Case in Shear Demand Load Duration Factor for Governing Load Case in Bearing Demand LC =str k 1 Σw + ΣP kN V ∗ kN M∗ kN ⋅ m N∗ kN LC =sserv Σw + ΣP kN Δ s mm LC =lserv Σw + ΣP kN Δ l mm M /k =d 1 60.2 kN ⋅ m V /k =d 1 68.9 kN N /k =d,gov 1 114 kN LC /k =str 1 k 1 (Σw + ΣP)/k 1 kN V /k ∗ 1 kN M /k ∗ 1 kN ⋅ m N /k ∗ 1 kN k =1,M∗ 0.8 k =1,V ∗ 0.8 k =1,N∗ 0.8 Strength Load Case Analysis with Constant Capacity 11
- 12. Unfactored Load Load TypeTotal Load ( ) Shear ( ) Moment ( ) Max Reaction ( ) Short-Term Deflection ( ) G 13.6 -3.78 -3.29 7.38 -2.19 Q 30.5 9.01 -7.53 16.3 -6.17 Bearing Utilisation Support Location ( ) Bearing Demand ( ) Bearing Factor Bearing Capacity ( ) Bearing Utilisation 0 6.55 1 103 0.0634 3 000 41.6 1.1 114 0.366 8 500 29.5 1.1 114 0.26 Short-Term Deflection Per Span Span Length ( ) Span Type Short-Term Deflection ( ) Short-term Deflection Limit ( ) Deflection Utilisation 3 000 Int -0.381 10 0.0381 5 500 Int -6.49 10 0.649 1 500 Cant 4.1 10 0.41 Long-Term Deflection Per Span Span Length ( ) Span Type Long-Term Deflection ( ) Long-term Deflection Limit ( ) Deflection Utilisation 3 000 Int -0.542 10 0.0542 5 500 Int -9.32 10 0.932 1 500 Cant 5.87 10 0.587 Imposed Load Deflection Per Span Span Length ( ) Span Type Imposed Load Deflection ( ) Imposed Load Deflection Limit ( ) Deflection Utilisation 3 000 Int 0.516 10 0.0516 5 500 Int -6.17 10 0.617 1 500 Cant 3.92 10 0.392 Comments Beam is not notched Default equilibrium moisture content is 15% (most non-exposed use) Default fully-loaded moisture content is less than 25% (most non-exposed use) Σw + ΣP kN V ∗ kN M∗ kN ⋅ m R∗ kN Δ s mm N =d,table l mm N /k ∗ 1 kN k 7 N /k d 1 kN N /N ∗ d D =ST L mm Δ s mm Δ s,lim mm Δ /Δ s s,lim D =LT L mm Δ l mm Δ l,lim mm Δ /Δ l l,lim D =Q L mm Δ Q mm Δ Q,lim mm Δ /Δ Q Q,lim 1. 2. 3. Unfactored Load Analysis (AS1170.0) Bearing Capacity (AS 1720.1:2010, Cl 3.2.6) Deflection Analysis Comments Assumptions 12