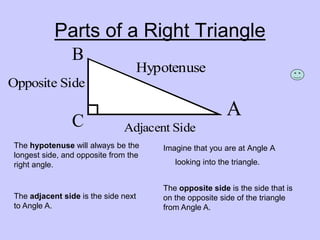
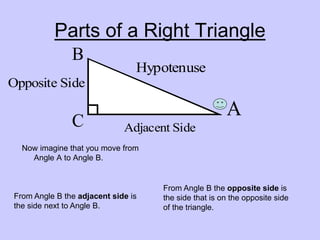
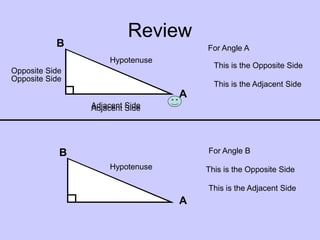
Trigonometric ratios relate the sides of a right triangle to an angle of the triangle. There are three basic ratios: sine, cosine, and tangent. Sine is the ratio of the opposite side to the hypotenuse. Cosine is the ratio of the adjacent side to the hypotenuse. Tangent is the ratio of the opposite side to the adjacent side. These ratios can be remembered using the mnemonic "SOH-CAH-TOA". Trigonometric ratios will be the same for any similar triangles, as the ratios of corresponding sides will be equivalent.

1. 9.4/9.5 Trig Ratios
EQ: How do I set up Trig Ratios in a right triangle?

2. Parts of a Right Triangle
A
Adjacent Side
C
Opposite Side
B
Hypotenuse
Imagine that you are at Angle A
looking into the triangle.
The adjacent side is the side next
to Angle A.
The opposite side is the side that is
on the opposite side of the triangle
from Angle A.
The hypotenuse will always be the
longest side, and opposite from the
right angle.

3. Parts of a Right Triangle
A
Adjacent Side
C
Opposite Side
B
Hypotenuse
Now imagine that you move from
Angle A to Angle B.
From Angle B the adjacent side is
the side next to Angle B.
From Angle B the opposite side is
the side that is on the opposite side
of the triangle.

4. Review
Hypotenuse
Hypotenuse
Opposite Side
Adjacent Side
A
B
For Angle A
This is the Opposite Side
This is the Adjacent Side
For Angle B
A
This is the Adjacent Side
This is the Opposite Side
Opposite Side
Adjacent Side
B

5. Trig Ratios
• Each of the 3 ratios has a name
• The names also refer to an angle
Opposite
Sine of Angle A =
Hypotenuse
Adjacent
Cosine of Angle A =
Hypotenuse
Opposite
Tangent of Angle A =
Adjacent
Hypotenuse
Adjacent
Opposite
A

6. Trig Ratios
B
Opposite
=
Hypotenuse
Adjacent
=
Hypotenuse
Opposite
=
Adjacent
Hypotenuse
Adjacent
Opposite
A
If the angle changes from A to B
The way the ratios are made is the
same
B
B
B
Cosine of Angle
Sine of Angle
Tangent of Angle

7. SOHCAHTOA
Adjacent
A
B
Opposite
Hypotenuse
Here is a way to remember how
to make the 3 basic Trig Ratios
1) Identify the Opposite and Adjacent
sides for the appropriate angle
2) SOHCAHTOA is pronounced “Sew Caw Toe A” and it means
Sin is Opposite over Hypotenuse, Cos is Adjacent over Hypotenuse,
and Tan is Opposite over Adjacent
Put the underlined letters to make
SOH-CAH-TOA

8. Examples of Trig Ratios
Sin P
Cos P
12
20
16
Q
P
Tan P Tan Q
Cos Q
Sin Q
16
20

12
20

16
12

12
20

16
20

12
16

First we will find the Sine, Cosine and
Tangent ratios for Angle P.
Next we will find the Sine, Cosine, and
Tangent ratios for Angle Q
Opposite
Adjacent
Remember SohCahToa

9. Similar Triangles and Trig Ratios
ABC QPR

3
5
4
A
B
12
20
16
Q
P
R
C
They are similar triangles, since
ratios of corresponding sides are
the same
Let’s look at the 3 basic Trig
ratios for these 2 triangles
Tan Q
Cos Q
Sin Q
12
20

16
20

12
16
 Tan A
Cos A
Sin A
3
5

4
5

3
4

Notice that these ratios are equivalent!!

10. Similar Triangles and Trig Ratios
• Triangles are similar if the ratios of the
lengths of the corresponding side are the
same.
• Triangles are similar if they have the same
angles
• All similar triangles have the same trig
ratios for corresponding angles