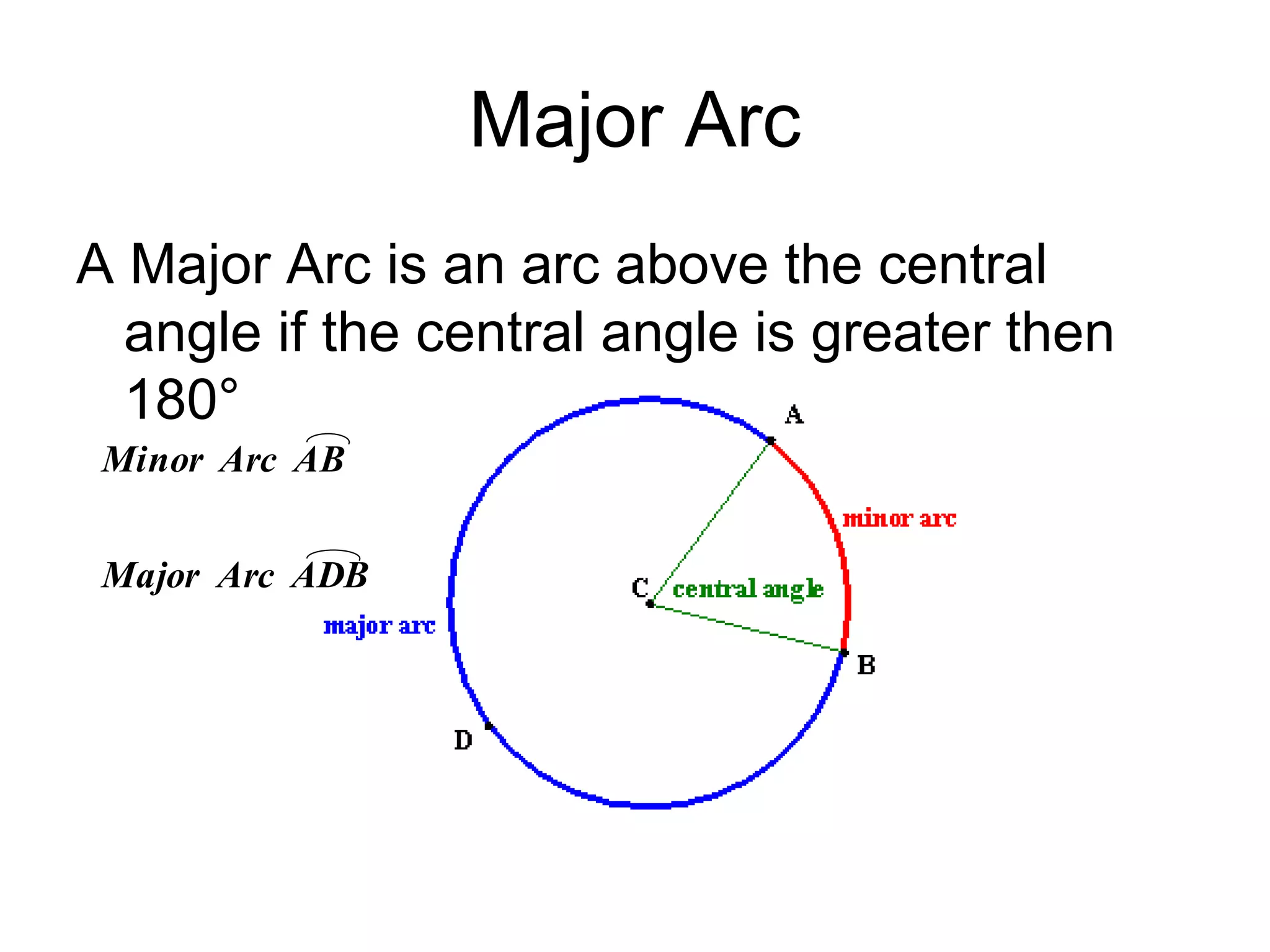
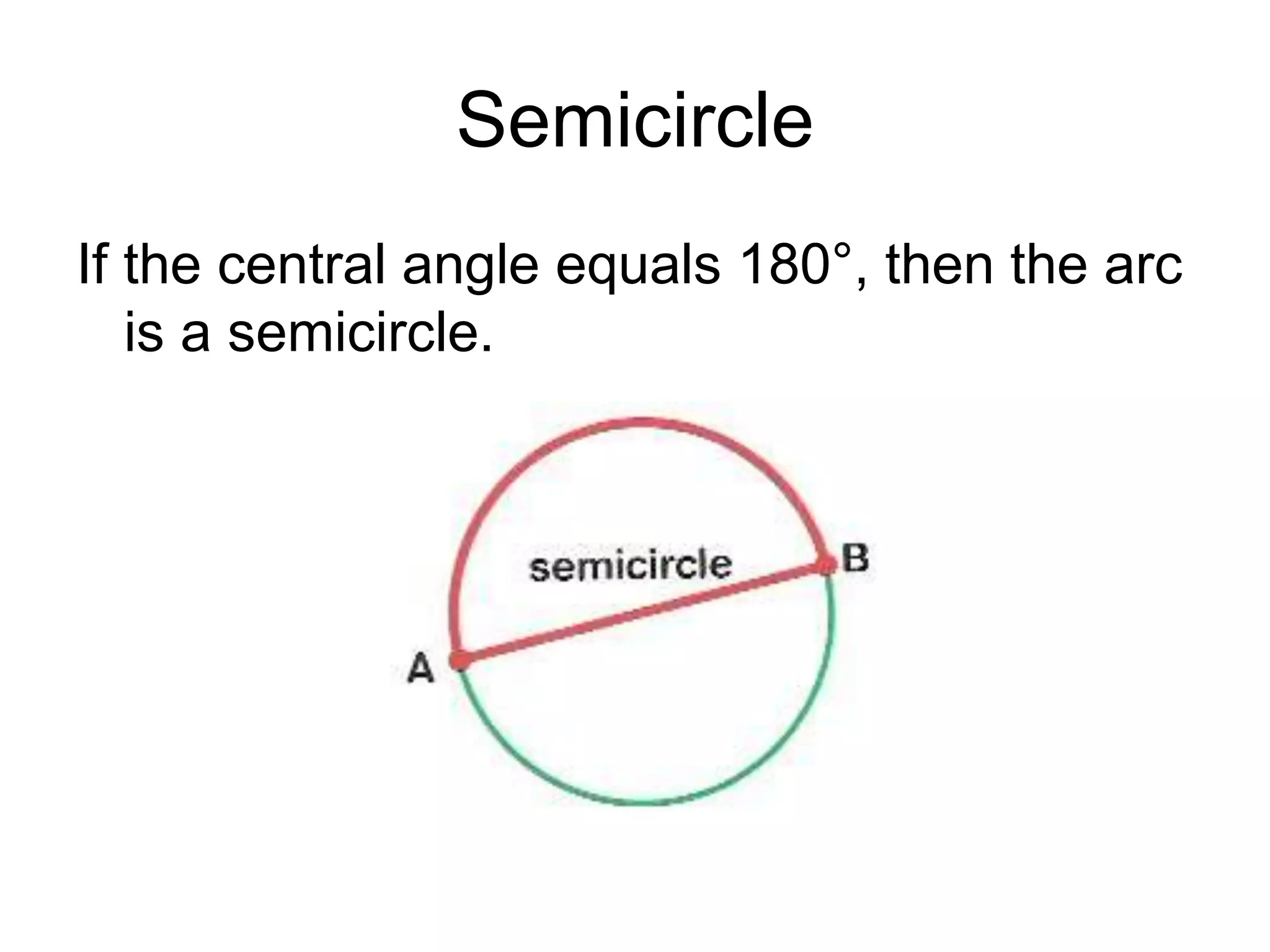
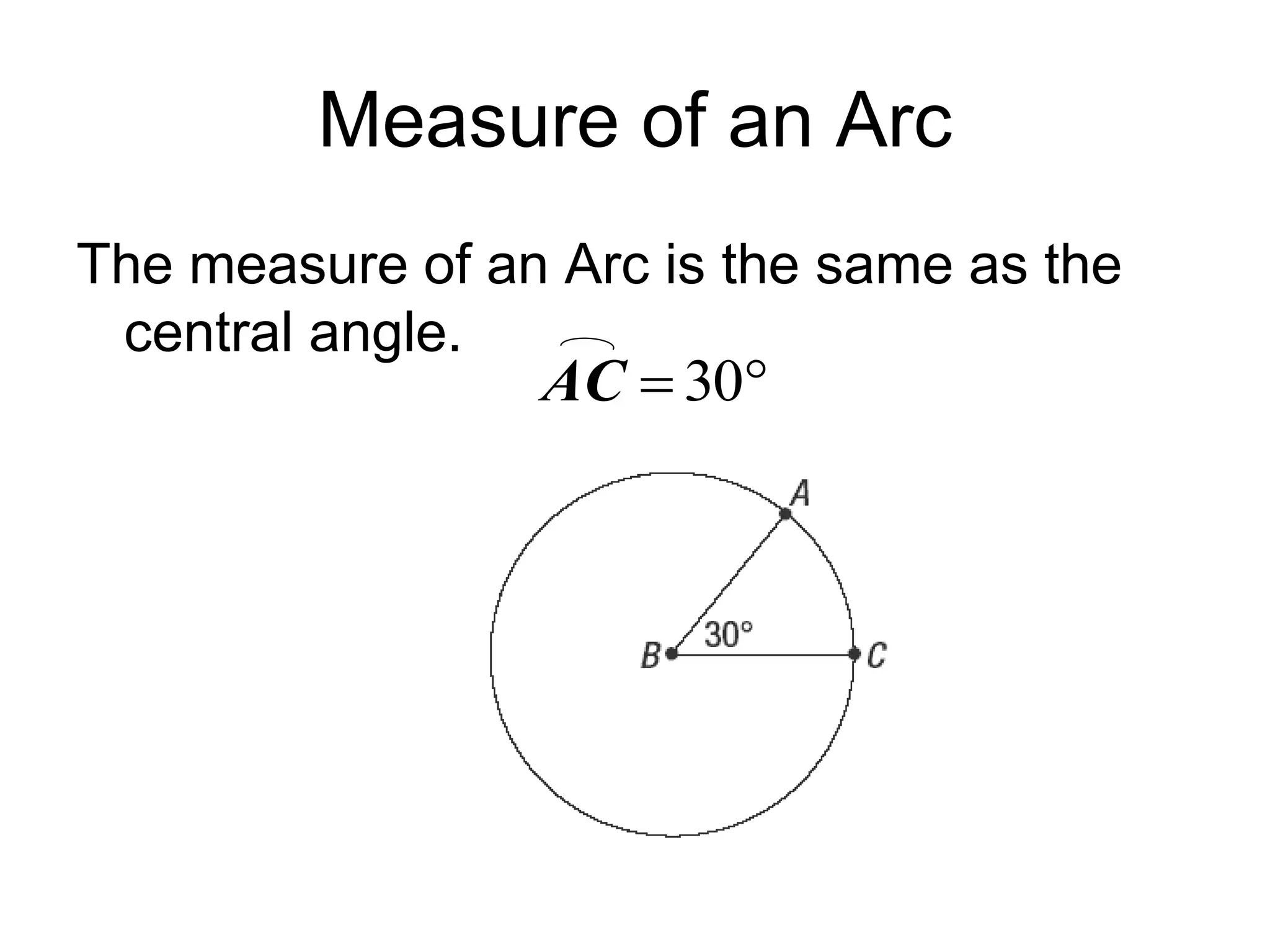
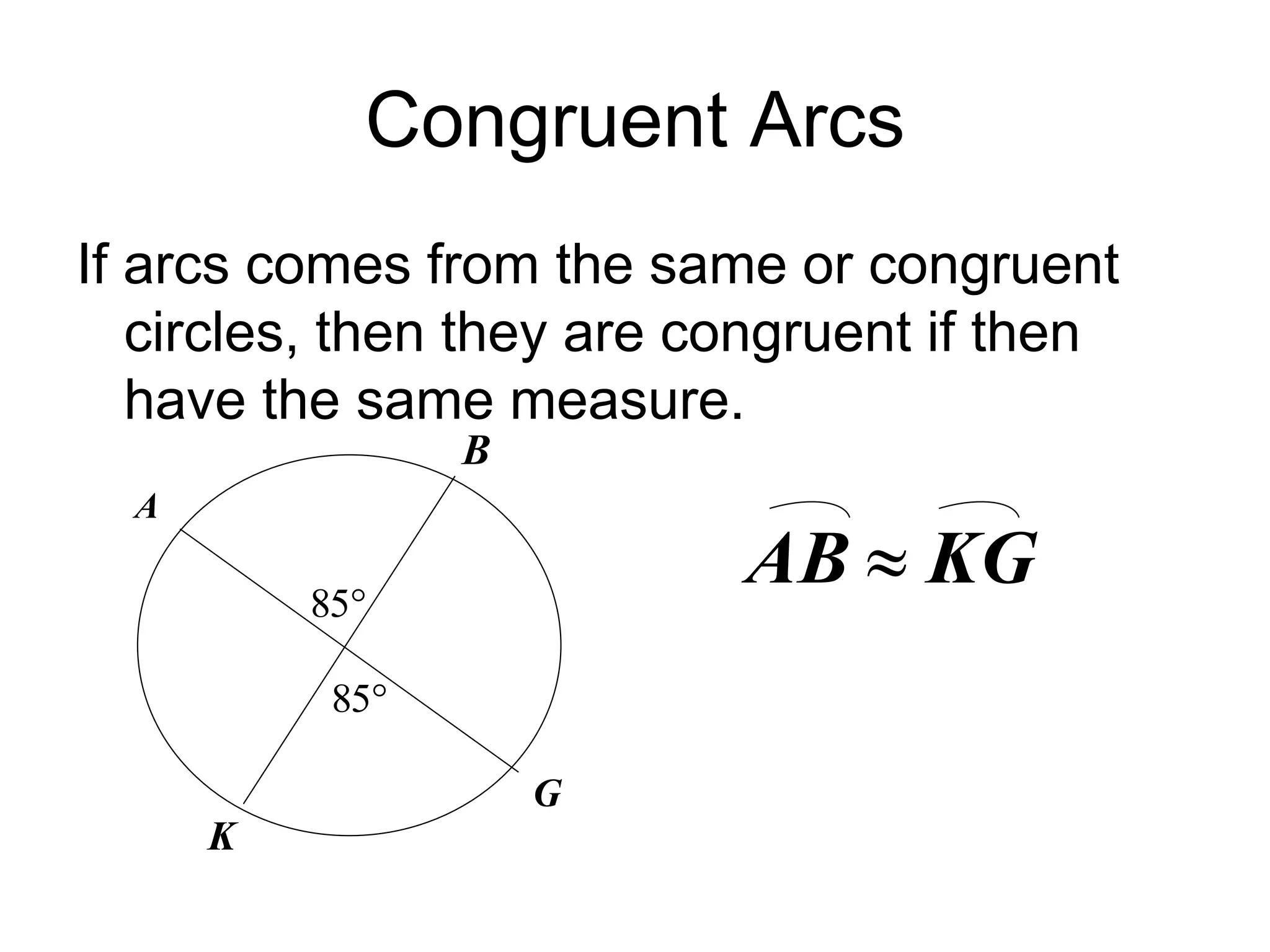
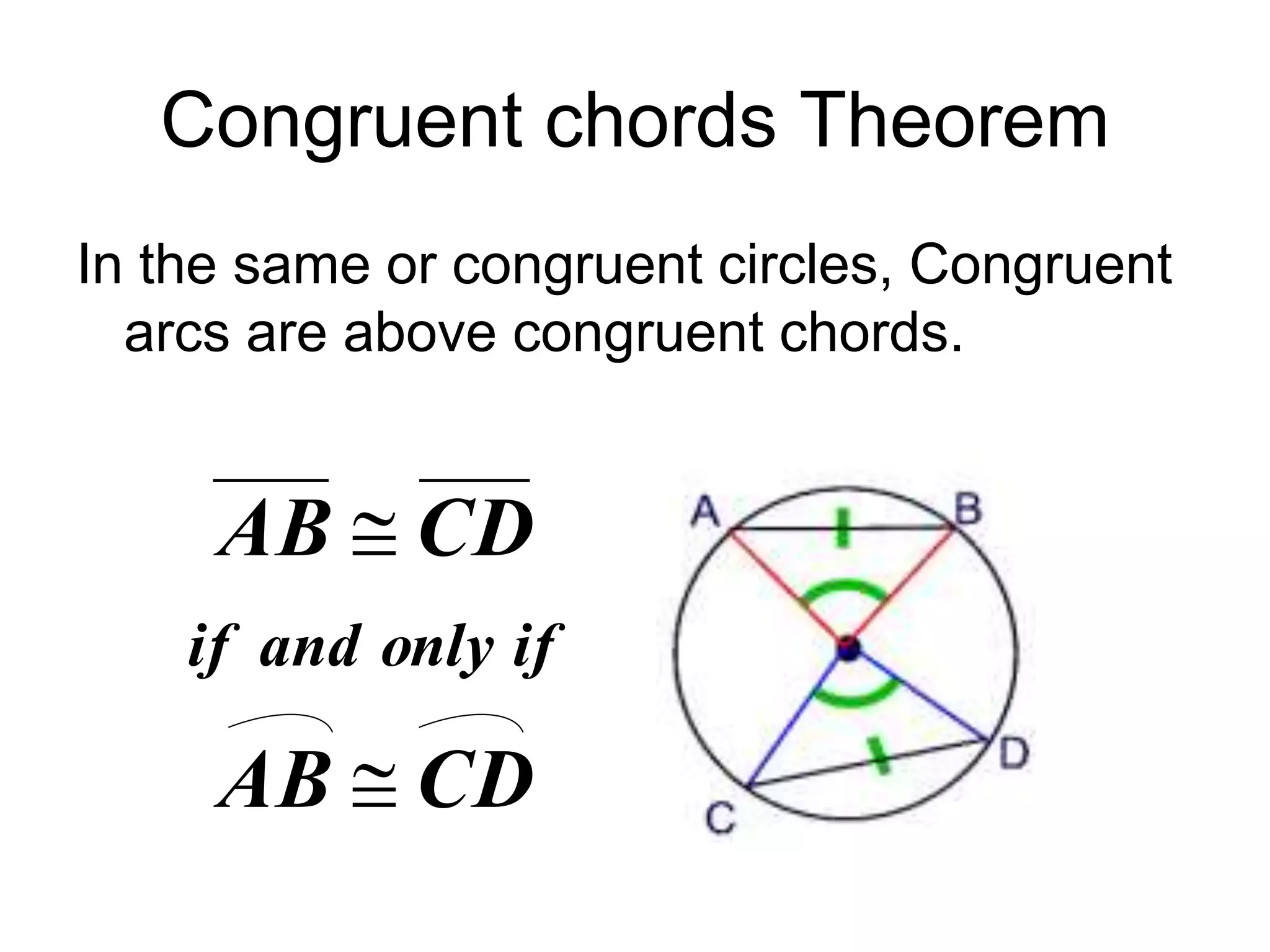
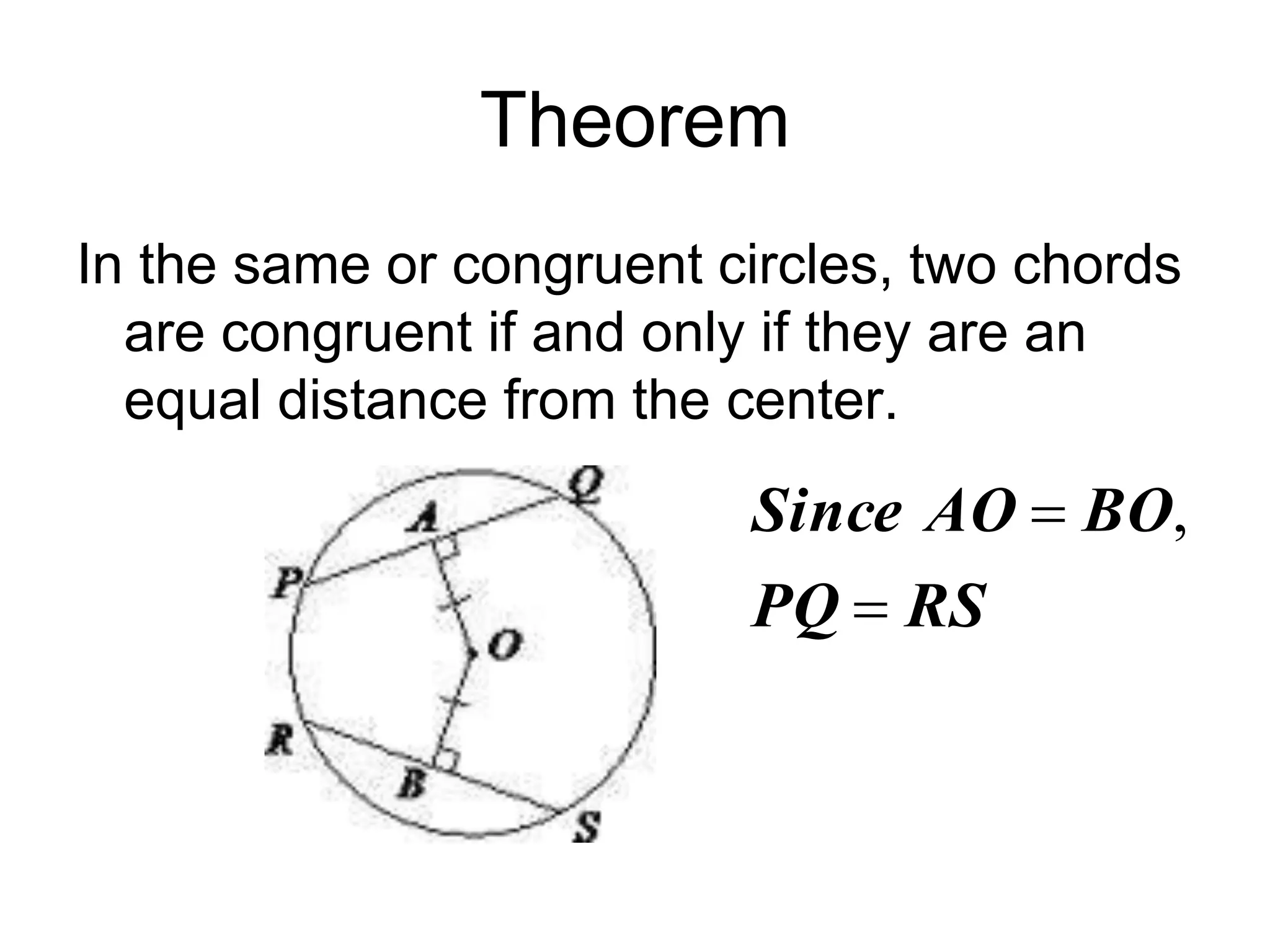
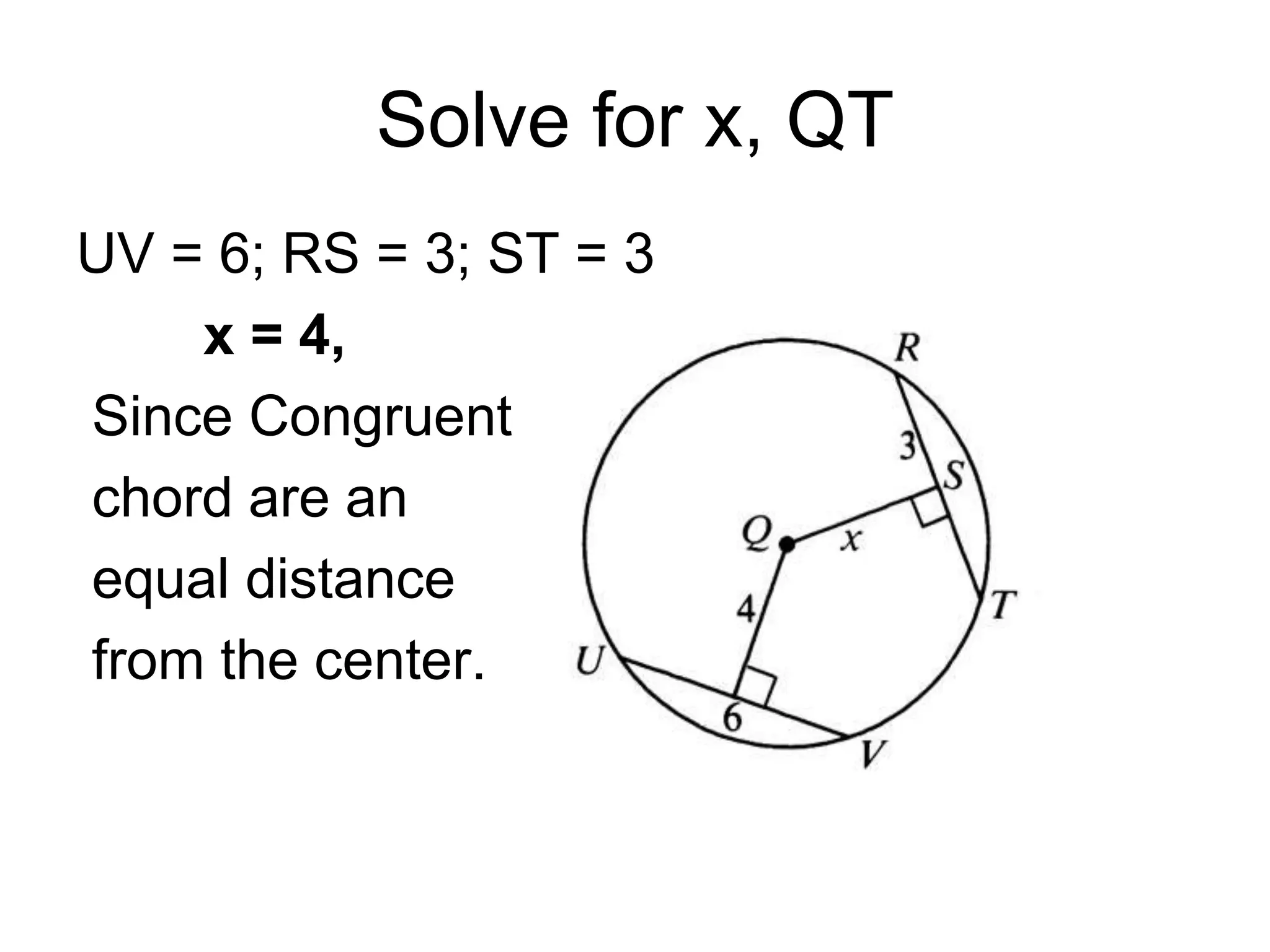
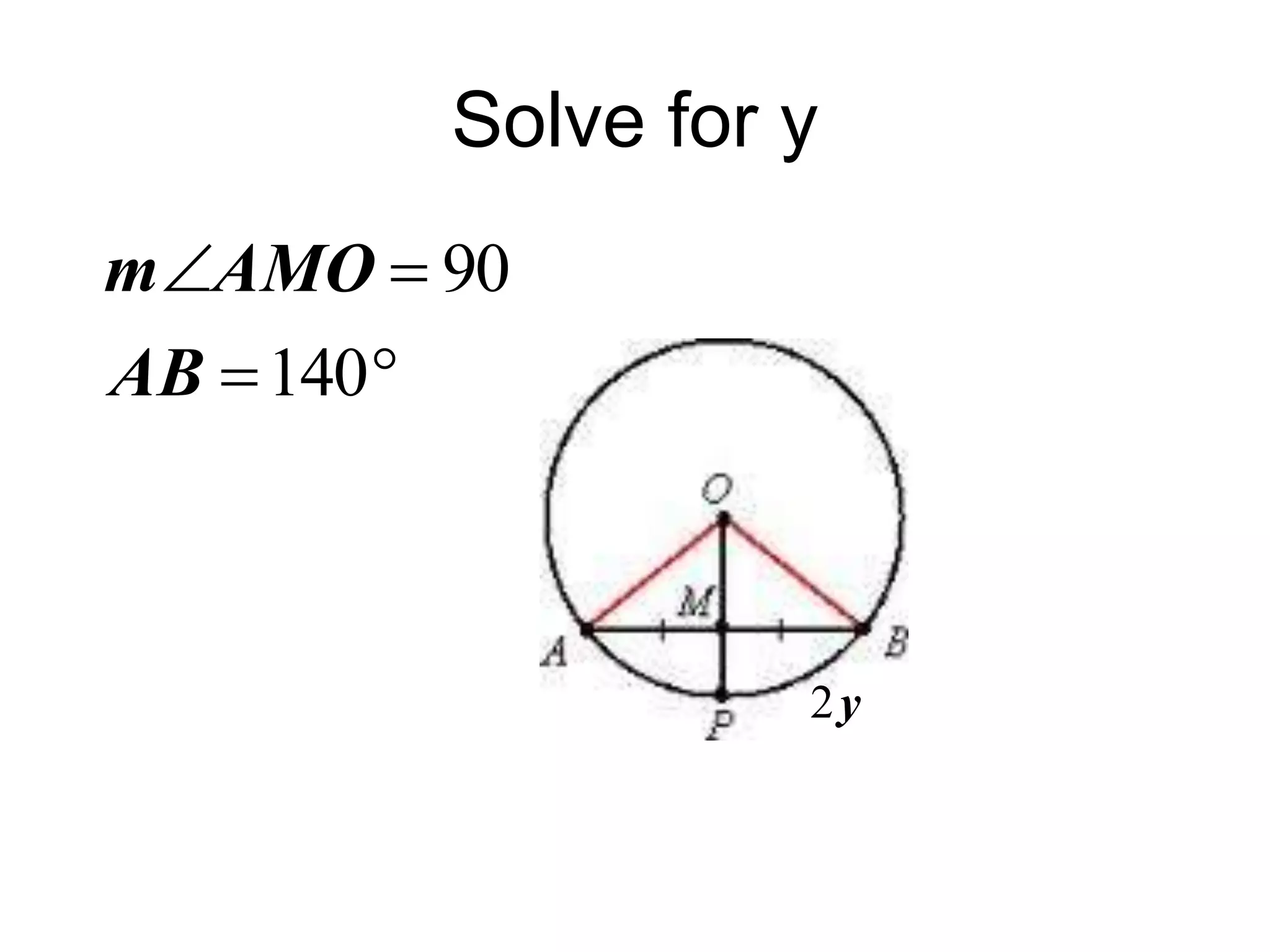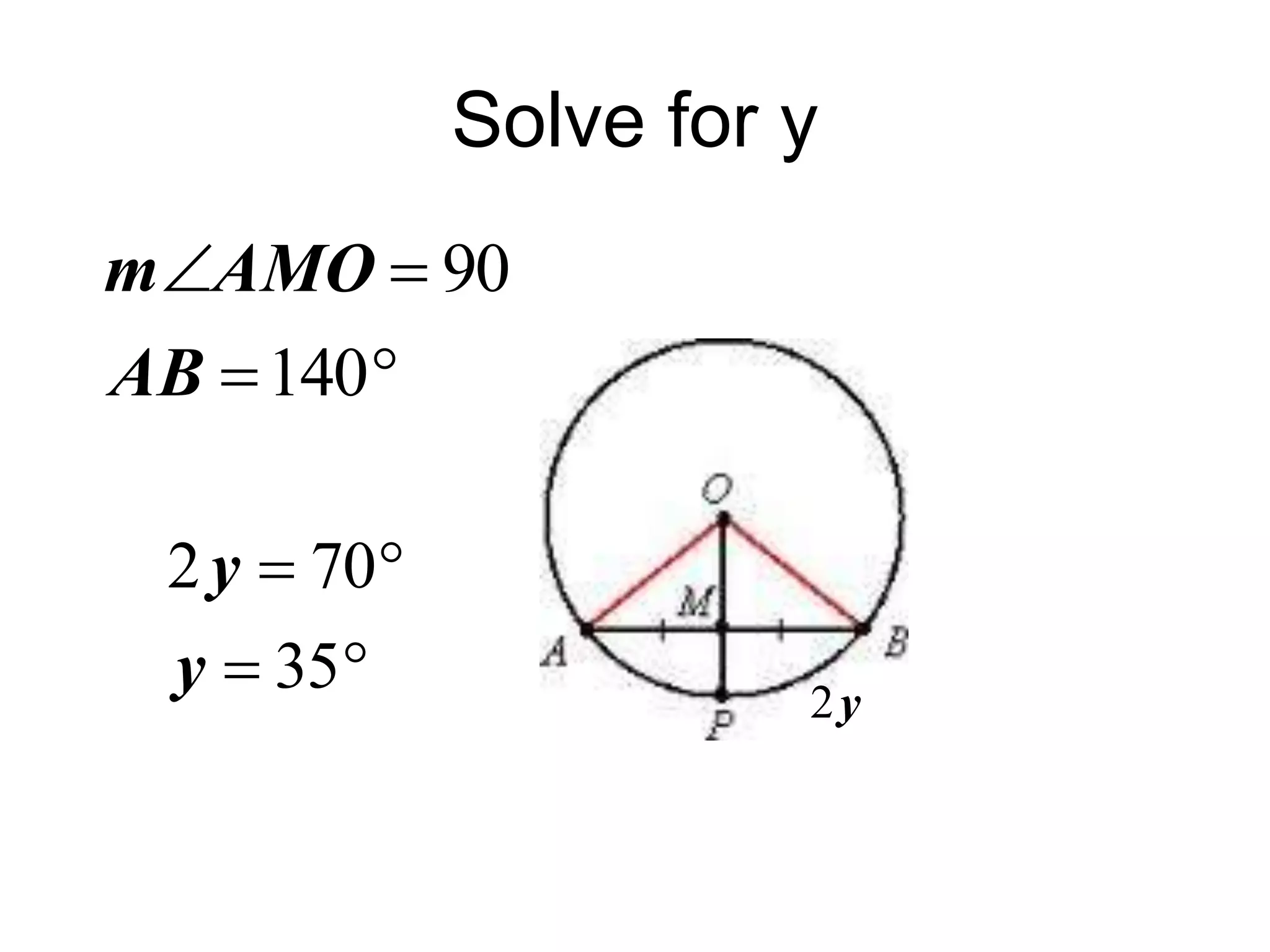This document discusses arcs and chords in circles. It defines central angles, minor arcs, major arcs, and semicircles. It states that the measure of an arc is equal to the measure of its central angle. Arcs can be added together. Congruent arcs have the same measure and are above congruent chords. If a diameter is perpendicular to a chord, it bisects the chord and arc. The document also includes theorems about chords and solving problems involving arcs and chords. It concludes with homework problems assigning specific exercise numbers to complete.

1. 10.2 Arcs and Chords
Central angle
Minor Arc
Major Arc

2. Central angle
A central angle is an angle which vertex is
the center of a circle

3. Minor Arc
An Arc is part of the circle.
A Minor Arc is an arc above the central
angle if the central angle is less then 180°

4. Major Arc
A Major Arc is an arc above the central
angle if the central angle is greater then
180°
ADB
Arc
Major
AB
Arc
Minor

5. Semicircle
If the central angle equals 180°, then the arc
is a semicircle.

6. Semicircle
If the central angle equals 180°, then the arc
is a semicircle.

7. Measure of an Arc
The measure of an Arc is the same as the
central angle.

 30
AC

8. Measure of an Arc
The measure of an Arc is the same as the
central angle.

120
AB






240
120
360
ADB
ADB
D
A
B

9. Postulate: Arc Addition
Arcs can be added together.






110
27
83
QR
RP
QP

83

27

10. Congruent Arcs
If arcs comes from the same or congruent
circles, then they are congruent if then
have the same measure.
A
B
K
G

85

85
KG
AB 

11. Congruent chords Theorem
In the same or congruent circles, Congruent
arcs are above congruent chords.
CD
AB
CD
AB


if
only
and
if

12. Theorem
If a diameter is perpendicular to a chord ,
then it bisects the chord and its arc.
BC
AC
BE
AE



13. Theorem
If a chord is the perpendicular bisector of
another chord (BC), then the chord is a
diameter.
EC
BE
DC
BD



14. Solve for y




140
90
AB
AMO
m
y
2

15. Solve for y




140
90
AB
AMO
m
y
2




35
70
2
y
y

16. Theorem
In the same or congruent circles, two chords
are congruent if and only if they are an
equal distance from the center.
RS
PQ
BO
AO
Since

 ,

17. Solve for x, QT
UV = 6; RS = 3; ST = 3

18. Solve for x, QT
UV = 6; RS = 3; ST = 3
x = 4,
Since Congruent
chord are an
equal distance
from the center.

19. Solve for x, QT
UV = 6; RS = 3; ST = 3
x = 4,
5
9
16
3
4 2
2
2





QT
QT 4

20. Find the measure of the arc
Solve for x and y

52

52
 
 6
2y
 
10
x

21. Find the measure of the arc
Solve for x and y

52

52
 
 6
2y
 
10
x
23
2
46
)
6
2
(
52
44
10
52









y
y
y
x
x

22. Homework
Page 607 – 608
# 12 - 38

23. Homework
Page 608 -609
# 39 – 47,
49 – 51,
69, 76 - 79