Group 3 measures of central tendency and variation - (mean, median, mode, range standard deviation and variance)


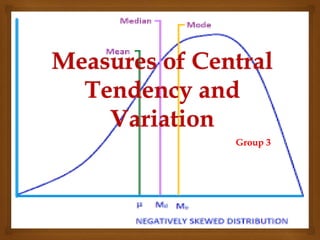
Measures of Central
Tendency and Variation
Central tendency: indicates where the center of
the distribution tends to be
(88% grade)
(compact, disperse)
Measures of central tendency answers whether
the scores are generally high or general low.


Measures of Central
Tendency and Variation
Average Height is 6’4” Average Height is 5’4”


Use of Central Tendency
 Simplification: one number
 Prediction: Predict other scores
Chairs, Classrooms, Books, School needs.
 Determining which off central
tendency to use depends on:
Scale of measurement
Nominal, Ordinal, interval,
Ratio
(NOIR)
Shape of Distribution
Skew
Kurtosis
Average Children: 2.3

Prepared by :
Mrs. Analie M. Sunga


Median is what divides the scores in
the distribution into two equal parts.
Fifty percent (50%) lies below the
median value and 50% lies above the
median value.
It is also known as the middle score or
the 50th percentile.
MEDIAN


The median is a single value from the data
set that measures the central item in the data.
This single value is the middlemost or most
central item in the set of scores. Half of the
scores lie above this point and other half lie
below it.
MEDIAN


 MEDIAN OF UNGROUPED DATA
1. Arrange the scores(from lowest to highest or highest to
lowest).
2. If the data has odd numbered items, the median is middle
item of the array. However, if it has even number of items,
the median is the average of the two middle items.
MEDIAN


X (score)
19
17
16
15
10
5
2
Example 1:
Find the media score of 7 students in an
English class.

x(score)
30
19
17
16
15
10
5
2
Example 2:
Find the media score of 8 students in an
English class.
x=
16 +15
2
x= 15.5


MEDIAN OF GROUPED DATA
FORMULA:
𝑥 = 𝐿B +
𝑛
2
− 𝑐𝑓<
𝑓𝑚
× c.i
MEDIAN
𝒙 = median value
MC = median class is a category
containing
𝑛
2
LB = lower boundary of the
median class (MC)
cf< = cumulative frequency
before the median class if
the scores are arranged from
lowest to highest value
Fm = frequency of the median
class
c.i = size of the class interval
n= number of scores


1. Complete the table for <cf.
2. Get
𝑛
2
of the scores in the distribution
so that you can identify MC.
3. Determine LB, cfp, fm and c.i.
4. Solve the median using the formula.
Steps in Solving Median
for Grouped Data

X F <cf
10-14 5 5
15-19 2 7
20-24 3 10
25-29 5 15
30-34 2 17
35-39 9 26
40-44 6 32
45-49 3 35
50-54 5 40
n=40
Example:
Scores of 40 students in a science class consist of 60 items
and they are tabulated below. The highest score is 54
and the lowest score is 10.

𝑛
2
=
40
2
= 20 (The category containing
𝑛
2
is 35-39)
LB= 34.5 (Lower Limit of the MC = 35)
Cf<= 17
fm=9
c.I = 5
𝑥 = 𝐿B +
𝑛
2
− 𝑐𝑓<
𝑓𝑚
× c.i
= 34.5 +
20 − 17
9
× 5
= 34.5 +
15
9
𝑥 = 36.17
𝑥 = 𝐿B +
𝑛
2
− 𝑐𝑓<
𝑓𝑚
× c.i


Mode or Modal Score
is the measure of central tendency
that identifies the category or score
that occurs the most frequently
within the distribution of data


Classification of Mode
Unimodal- is a distribution of scores
that consist of only one mode.
Bimodal- is a distribution of scores
that consists of two modes.
Trimodal- is a distribution of scores
that consist of three modes or
multimodal a distribution of scores
that consists of more than two modes.


Example: Score of 10
students in Section
A,B and C (
Ungrouped Data)
A B C
25 25 25
24 24 25
24 24 25
20 20 22
20 18 21
20 18 21
16 17 21
12 10 18
10 9 18
7 7 18


Sample (Grouped Data)
x f
10-14 5
15-19 2
20-24 3
25-29 5
30-34 2
35-39 9
40-44 6
45-49 3
50-54 5
N=40
Scores of 40 students in a students in a science
class consist of 60 items and they are tabulated
below:


Terms
Lb= Lower boundary of the modal
class
Modal Class (MC)= is a category
containing the highest frequency
D1= difference between the frequency
of the modal class and the frequency
above it, when the scores are arranged
from lowest to highest.


D2= difference between the frequency
of the modal class and the frequency
below it, when the scores are arranged
from lowest to highest.
C.i size of class interval
= LB +
d1
d1 + d2
𝑥 𝐶. 𝑖X̂

Range
It is the difference between the
lowest and highest values.
Example: In 4,6,9,3,7 the lowest
value is 3, and the highest is 9.
Solution:
9 - 3 = 6


Standard deviation
 It is a number used to tell how measurements
for a group are spread out from the average
(mean) or expected value.
 Low standard deviation means that most of
the numbers are close to the average.
 High standard deviation means that the
numbers are more spread out .


Standard deviation for
ungrouped data
SD= Standard deviation
∑= sum of
X= each value in the data set
X= mean of all values in the data set
n= number of value in the data set


How to Calculate the
Standard Deviation for
Ungrouped Data
1.Find the Mean.
2.Calculate the difference between each score
and the mean.
3.Square the difference between each score and
the mean.


Ungrouped Data
4.Add up all the squares of the difference
between each score and the mean.
5.Divide the obtained sum by n – 1.
6.Extract the positive square root of the
obtained quotient.


Find the standard
deviation


Grouped Data
1.Calculate the mean.
2.Get the deviations by finding the difference of
each midpoint from the mean.
3.Square the deviations and find its summation.
4.Substitute in the formula.


Find the standard
deviation
100 99 106 86 104 113 103 98 105 95 79
101 92 103 91 124 89 100 105 87 110
122 95 118 96 104 108 84 113 99 93 109
102 106 80 116 90 111 101 115 110 109
78 88 107 114 75 127 102 72


How to get class
intervals
Class Limits/ Interval
Range= Highest – Lowest
= 127- 72
= 55


How to get number of
class
Number of Class= ( Range ÷ Class Size) +
1
= (55 ÷ 5 )
+ 1
= 12
Class Limits/ Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74


How to get midpoint
 Midpoint(X)= (upper
limit +lower limit) ÷ 2
=
(125 + 129) ÷ 2
=
127
Class Limits/
Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74
Midpoint
127
122
117
112
107
102
97
92
87
82
77
72


Frequency
Class Limits/
Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74
Midpoint
127
122
117
112
107
102
97
92
87
82
77
72
Frequency
1
2
3
6
8
10
6
4
4
2
3
1
N= 50


Class Limits/
Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74
Midpoint
127
122
117
112
107
102
97
92
87
82
77
72
Frequency
1
2
3
6
8
10
6
4
4
2
3
1
N= 50
fX
127
244
351
672
856
1020
582
368
348
164
231
72
∑fX= 5035


Class Limits/
Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74
Midpoint
127
122
117
112
107
102
97
92
87
82
77
72
Frequency
1
2
3
6
8
10
6
4
4
2
3
1
N= 50
fX
127
244
351
672
856
1020
582
368
348
164
231
72
∑fX= 5035
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35


Class
Limits/
Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74
Midpoint
127
122
117
112
107
102
97
92
87
82
77
72
Frequenc
y
1
2
3
6
8
10
6
4
4
2
3
1
N= 50
fX
127
244
351
672
856
1020
582
368
348
164
231
72
∑fX= 5035
X
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
Mp-
X
76.6
5
71.6
5
66.6
5
61.6
5
56.6
5
51.6
546.
65
41.6
5
36.6


Class
Limits/
Interval
125- 129
120- 124
115- 119
110-114
105- 109
100- 104
95- 99
90- 94
85-89
80-84
75- 79
70- 74
Midpoint
127
122
117
112
107
102
97
92
87
82
77
72
Frequenc
y
1
2
3
6
8
10
6
4
4
2
3
1
N= 50
fX
127
244
351
672
856
1020
582
368
348
164
231
72
∑fX= 5035
X
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
50.35
(mp-
x)²
587.22
5133.7
2
4442.2
2
3800.7
2
2667.7
2
2176.2
2
1734.7
2
1343.7
2
1001.7
Mp-
X
76.6
5
71.6
5
66.6
5
61.6
5
56.6
5
51.6
546.
65
41.6
5
36.6


(mp-
x)²
587.22
5133.7
2
4442.2
2
3800.7
2
2667.7
2
2176.2
2
1734.7
2
1343.7
2
1001.7
F(mp-x) ²
5875.22
10267.45
13326.67
22804.34
25673.78
26677.23
13057.34
6938.89
5372.89
2003.44
2130.67
468.72
∑f(mp-x) ²
= 134596.6
SD= √134596.6
50-2
= √ 134596.6
49
= √2746.86
= 52.41


Variance
is the square of the standard deviation.
It is a measure of how dispersed or spread out the
set is, something that the “average” (mean or
median) is not designed to do.


Variance of ungrouped
data


Variance for Ungrouped
Data
1.Find the Mean.
2.Calculate the difference between each score and the
mean.
3.Square the difference between each score and the
mean.
4.Add up all the squares of the difference between
each score and the mean.
5.Divide the obtained sum by n – 1


Variance for Grouped Data
1.Calculate the mean.
2. Get the deviations by finding the
difference of each midpoint from the
mean.
3.Square the deviations and find its
summation.
4.Substitute in the formula.


Find the variance
s²= √134596.6
50-2
s² = √ 134596.6
49
s² = 2746.86


 Jonathan Profeta
 Analie Sunga
 Reymart Tabelisma
 Valerio, Pammelle
Group 3

Group 3 measures of central tendency and variation - (mean, median, mode, range standard deviation and variance)

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Group 3 measures of central tendency and variation - (mean, median, mode, range standard deviation and variance)

Similar to Group 3 measures of central tendency and variation - (mean, median, mode, range standard deviation and variance) (20)

Recently uploaded

Recently uploaded (20)

Group 3 measures of central tendency and variation - (mean, median, mode, range standard deviation and variance)