The document discusses matrix chain multiplication and algorithms for finding the optimal parenthesization of matrices. It explains that the product of matrices is associative but different parenthesizations may have different costs. It presents an algorithm called MATRIX-CHAIN-ORDER that uses dynamic programming to find a parenthesization with minimum calculation cost in O(n^3) time by trying all possible split points. The algorithm returns both the minimum cost and the optimal splitting positions.

1. Md. Mosharof Hosen
Id # 151002051

2. Matrix Chain Multiplication
 Matrix multiplication is assosiative and so all
parenthesizations yield the same product.
 For example, if the chain of matrices is
then the product can be fully
paranthesized in five distinct way:
(A1(A2(A3A4)))
(A1((A2A3)A4))
((A1A2)(A3A4))
((A1(A2A3))A4)
(((A1A2)A3)A4)
4321 AAAA
421 ...AAA

3. Matrix Multiply
MATRIX-MULTIPLY (A,B)
if columns [A] ≠ rows [B]
then error “incompatible dimensions”
else for i←1 to rows [A]
do for j←1 to columns [B]
do C[i, j]←0
for k←1 to columns [A]
do C[ i, j ]← C[ i, j] +A[ i, k]*B[ k, j]
return C

4. Example:
For example, we are going to multiply 4 matrices:
M1 = 2 x 3
M2 = 3 x 4
M3 = 4 x 5
M4 = 5 x 7
And we have conditions for multiplying matrices:
• We can multiply only two matrices at a time.
• When we go to multiply 2 matrices, the number of
columns of 1st matrix should be same as the
number of rows of 2nd matrix.

5. We can multiply the chain of matrix by
following those conditions in these ways:
M1 = 2 x 3
M2 = 3 x 4
M3 = 4 x 5
M4 = 5 x 7
( M1 M2 )( M3 M4 ) = 220
(( M1 M2 ) M3 ) M4 = 134
M1 ( M2 ( M3 M4 ) = 266
( M1 ( M2 M3 )M4 = 160
M1 (( M2 M3 )M4 ) = 207

6. The structure of an optimal paranthesization
 Let Ai...j where i ≤ j, denote the matrix product
Ai Ai+1 ... Aj
 Any parenthesization of Ai Ai+1 ... Aj must split
the product between Ak and Ak+1 for i ≤ k < j
Example: k = 4 (A1A2A3A4)(A5A6)
Total Cost of computing A[i,j] = minimum cost of A1..k
and Cost of computing Ak+1..j + Cost of multiplying
A1..k * Ak+1..j

7. Algorithm to Optimal Cost
MATRIX-CHAIN-ORDER(p[ ], n)
for i ← 1 to n
m[i, i] ← 0
for l ← 2 to n
for i ← 1 to n-l+1
j ← i+l-1
m[i, j] ← 
for k ← i to j-1
q ← m[i, k] + m[k+1, j] + p[i-1] p[k] p[j]
if q < m[i, j]
m[i, j] ← q
s[i, j] ← k
return m and s

8. Recursively def. value of opt. solution
Recursive defination for the minimum cost of
paranthesization:
We also keep track of optimal splits:









jipppjkmkim
ji
jim
jki
jki
if}],1[],[min
if0
],[
1

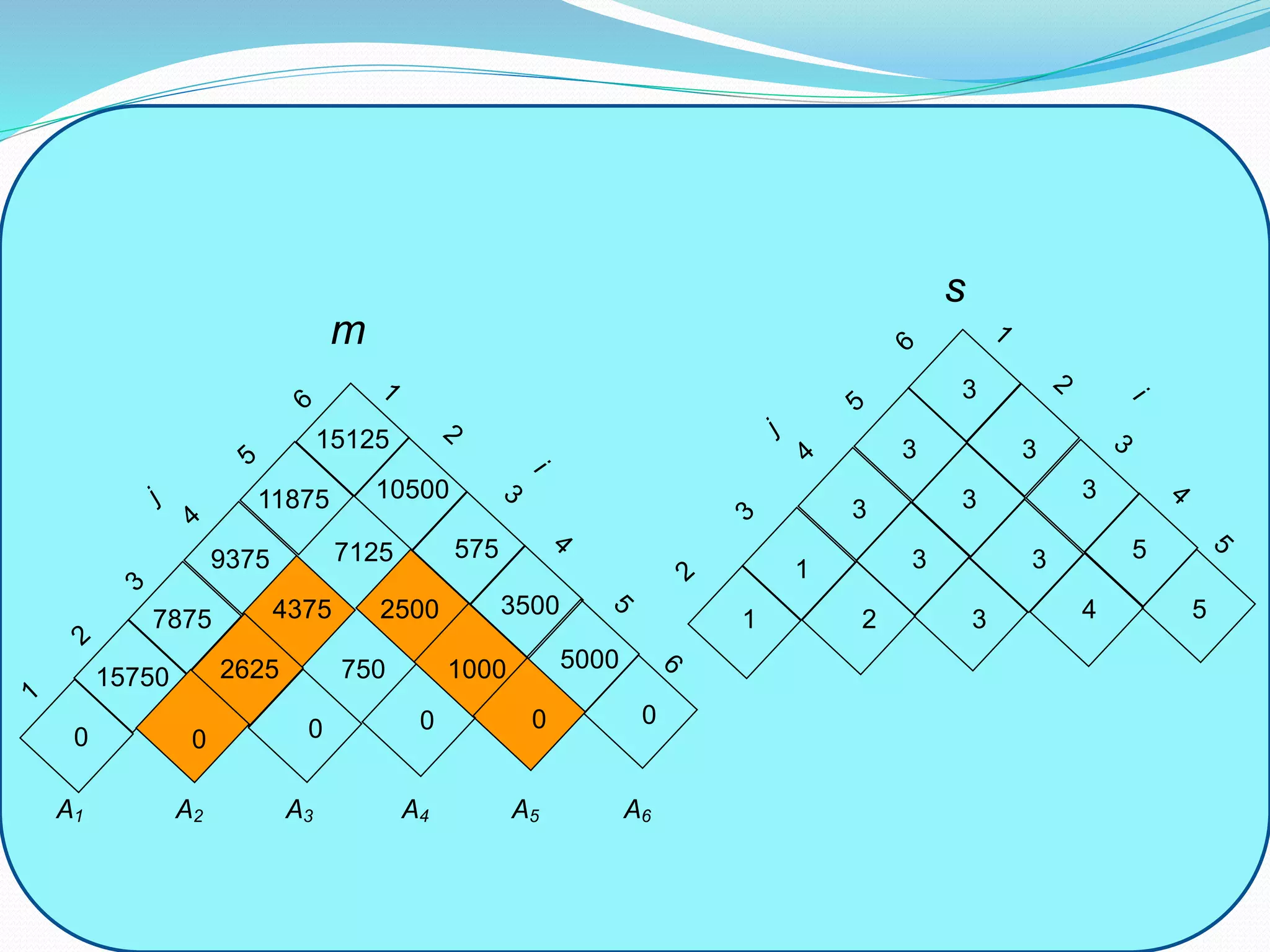
9. Example of Matrix Chain Multiplication
matrix dimension
A1 30 x 35
A2 35 x 15
A3 15 x 5
A4 5 x 10
A5 10 x 20
A6 20 x 25
 7125
11375201035043754]5,5[]4,2[
7125205351002625]5,4[]3,2[
1300020153525000]5,3[]2,2[
min]5,2[
51
531
521










pppmm
pppmm
pppmm
m

10. 15750
0
9375
7875
15125
11875
4375
2625
10500
7125
0
00
575
2500
0
50001000
3500
0
750
3
3
3
3 3
3 3
31
5
21 3 4 5
A1 A2 A3 A4 A5 A6
m
s
1000
2500