The document discusses the problem of determining the optimal way to fully parenthesize the product of a chain of matrices to minimize the number of scalar multiplications. It presents a dynamic programming approach to solve this problem in four steps: 1) characterize the structure of an optimal solution, 2) recursively define the cost of an optimal solution, 3) compute the costs using tables, 4) construct the optimal solution from the tables. An example is provided to illustrate computing the costs table and finding the optimal parenthesization of a chain of 6 matrices.

1. Matrix - Chain Multiplication
Dr. Kiran K
Assistant Professor
Department of CSE
UVCE
Bengaluru, India.

2. Introduction
Problem Statement:
Given a chain of n matrices <A1, A2, . . . , An>,
Ai has dimension pi-1 x pi , (i = 1, 2, . . . , n)
Fully Parenthesize the product A1 A2 . . . An in a way that Minimizes the number of
Scalar Multiplications.
Fully Parenthesize:
 A product of matrices is Fully Parenthesized if it is either
• A Single Matrix or
• Product of Two Fully Parenthesized Matrix Products, surrounded by
parentheses.

3. Eg.:
The product A1A2A3A4 of the matrices <A1, A2, A3, A4>, can be Fully
Parenthesized in Five distinct ways:
• (A1(A2 (A3A4)))
• (A1((A2A3) A4))
• ((A1A2)(A3A4))
• ((A1(A2A3))A4)
• (((A1A2)A3)A4)
Introduction…

4. MATRIX-MULTIPLY (A, B)
If (A.columns  B.rows)
Error “Incompatible Dimensions”
Else
Let C be a new A.rows x B.columns Matrix
For (i = 1 to A.rows)
For (j = 1 to B.columns)
cij = 0
For (k = 1 to A.columns)
cij = cij + aik . bkj
return C
Order of A: i x k
Order of B: k x j
Order of C: i x j
Number of Scalar Multiplications:
k multiplications for each of the
(i * j) entries of C.
= i * k * j
= i k j
Multiplication of Two Matrices

5. Eg.:
<A1, A2, A3>
A1 - 10 x 100
A2 - 100 x 5
A3 - 5 x 50
Cost of Matrix Multiplication
((A1A2) A3)
A1A2 - 10 * 100 * 5 = 5000
((A1A2) A3) – 10 * 5 * 50 = 2500
Total 5000 + 2500
= 7500 Scalar Multipliations
(A1 (A2A3))
A2A3 – 100 * 5 * 50 = 25000
(A1 (A2A3) – 10 * 100 * 50 = 50000
Total 25000 + 50000
= 75000 Scalar Multiplications
Parenthesizing a chain of matrices can have a dramatic impact on the cost of product
evaluation.

6. Goal:
To determine an
Order for Multiplying Matrices
that has the
Lowest Cost

7. Let P(n) - Number of Alternative Parenthesizations of a sequence of n matrices.
• n = 1, Only one matrix:
• Only one way to fully parenthesize the matrix product.
• n > = 2:
• A Fully Parenthesized matrix product is the Product of Two Fully
Parenthesized Matrix Subproducts.
• Split between the two subproducts may occur between the kth and (k + 1)st
matrices for any k = 1, 2, . . . , n - 1.
Counting the Number of Parenthesizations

8. Dynamic-programming method is used to determine how to optimally parenthesize
a matrix chain:
1. Characterize the structure of an optimal solution.
2. Recursively define the value of an optimal solution.
3. Compute the value of an optimal solution.
4. Construct an optimal solution from computed information
Optimal Parenthesization of Matrix-Chain

9. • Ai . . . j : Matrix that results from evaluating the product Ai Ai+1 . . . Aj. i  j.
• If (i < j)
Parenthesize Ai Ai+1 . . . Aj by splitting the product between Ak and Ak+1
for i  k < j.
→ Compute matrices Ai . . . k and Ak + 1 . . . j and then multiply them together to
produce the final product Ai . . . j.
• Cost of Parenthesizing = Cost of Computing Ai . . . k + Cost of Computing Ak + 1 . . . j
+ Cost of Multiplying them together.
1. Structure of an Optimal Parenthesization

10. • Cost of an optimal solution is defined recursively in terms of optimal solutions to
sub-problems.
• Sub-problems: Problems of determining the minimum cost of parenthesizing
Ai A i + 1 . . . A j for 1  i  j  n.
• m [i, j]: Minimum number of scalar multiplications to compute matrix Ai . . . j
 if (i = j)
There is only one matrix A i . . . i = A 1
m [i, j] = 0
 If (i < j)
m [i, j] = Cost of Computing Ai . . . k + Cost of Computing Ak + 1 . . . j +
Cost of Multiplying them together.
m [i, j] = m [i, k] + m [k + 1, j] + pi – 1 pk pj
2. A Recursive solution

11.  k varies from i to j – 1. Hence,
• s [i, j]: Value of k at which the Split is an Optimal Parenthesization.
A Recursive Solution…

12. • pi – 1 x pi - Dimension of matrix A i. i = 1, 2, . . . , n
• p = < p0 , p1 , . . . pn> - List of Matrix Dimensions.
• m [1 . . n, 1 . . n] - Table storing the Costs m [i, j]
• s [1 . . n - 1, 2 . . n] - Table storing the Index of k that achieved
optimal cost in computing m [i, j].
Used to construct an optimal solution.
• m [1, n] - Lowest cost to compute A 1 . . n
3. Computing the Optimal Costs

13. MATRIX-CHAIN-ORDER (p)
n = p.length - 1
let m [1 . . n, 1 . . n] and s [1 . . n - 1, 2 . . n] be new tables
For (i = 1 to n)
m [i, i] = 0
For (l = 2 to n)
For (i = 1 to n - l + 1)
j = i + l – 1
m [i, j] = 
For (k = i to j – 1)
q = m [i, k] + m [k + 1, j] + pi-1 pk pj
If (q < m [i, j])
m [i, j] = q
s [i, j] = k
return m and s
Computing the Optimal Costs…
Running Time : O (n3)
Space to store Tables m and s : O (n2)

14. Example
n = 6
pi = 30, 35, 15, 5, 10, 20, 25
Table m:
• Order: n x n
• i - rows and j - columns
• Only the lower half of the
table upto (i, i) gets filled
because 1  i  j  n
Matrix A1 A2 A3 A4 A5 A6
Dimension 30 x 35 35 x 15 15 x 5 5 x 10 10 x 20 20 x 25
1 2 3 4 5 6
1 0
2 0
3 0
4 0
5 0
6 0
If no. of matrices = 1, No. of ways to
parenthesize = 0. i.e., m (i, i) = 0
m [1, 1] = 0, m [2, 2] = 0, m [3, 3] = 0
m [4, 4] = 0, m [5, 5] = 0, m [6, 6] = 0
j
i
Tablem

15. Example…
• l = 2 → 2 Matrices
• Matrices: A1 A2, A2 A3, A3 A4, A4 A5, A5 A6
• No. of positions where split can occur = 1. Therefore, k = 1, 2, 3, 4, 5
respectively.
• Number of different parenthesizations:
A1 A2: m [1, 2] = m [1, 1] + m [2, 2] + p0 p1 p2 = 0 + 0 + 30 x 35 x 15 = 15,750
s [1, 2] = 1
A2 A3: m [2, 3] = m [2, 2] + m [3, 3] + p1 p2 p3 = 0 + 0 + 35 x 15 x 05 = 2,625
s [2, 3] = 2
A3 A4: m [3, 4] = m [3, 3] + m [4, 4] + p2 p3 p4 = 0 + 0 + 15 x 05 x 10 = 750
s [2, 3] = 3
A4 A5: m [4, 5] = m [4, 4] + m [5, 5] + p3 p4 p5 = 0 + 0 + 30 x 35 x 15 = 1,000
s [1, 2] = 4
A5 A6: m [5, 6] = m [5, 5] + m [6, 6] + p4 p5 p6 = 0 + 0 + 10 x 20 x 25 = 5,000
s [1, 2] = 5

16. Example…
n = 6; pi = 30, 35, 15, 5, 10, 20, 25; l = 2 i = 1 to n - l + 1; j = i + l – 1; k = i to j – 1
q = m [i, k] + m [k + 1, j] + pi-1 pk pj
i = 1
j = 1+2-1 = 2
i = 2
j = 2+2-1 = 3
i = 3
j = 3+2-1 = 4
k = 1
q = m [1,1] + m [2,2] + p0 p1 p2
= 0 + 0 + 30 x 35 x 15 = 15,750
k = 2
q = m [2,2] + m [3,3] + p1 p2 p3
= 0 + 0 + 35 x 15 x 5 = 2,625
k = 3
q = m [3,3] + m [4,4] + p2 p3 p4
= 0 + 0 + 15 x 5 x 10 = 750
m [1, 2] = 15,750
s [1, 2] = 1
m [2, 3] = 2,625
s [2, 3] = 2
m [3, 4] = 750
s [3, 4] = 3
i = 4
j = 4+2-1 = 5
i = 5
j = 5+2-1 = 6
k = 4
q = m [4,4] + m [5,5] + p3 p4 p5
= 0 + 0 + 30 x 35 x 15 = 1,000
k = 5
q = m [5,5] + m [6,6] + p4 p5 p6
= 0 + 0 + 10 x 20 x 25 = 5,000
m [4, 5] = 1,000
s [4, 5] = 4
m [5, 6] = 5,000
s [5, 6] = 5

17. Example…
1 2 3 4 5 6
1 0 15,750
2 0 2,625
3 0 750
4 0 1,000
5 0 5,000
6 0
j
i
Table m 1 2 3 4 5 6
1 1
2 2
3 3
4 4
5 5
Table s
j
i

18. Example…
• l = 3 → 3 Matrices
• Matrices: A1 A2 A3, A2 A3 A4, A3 A4 A5, A4 A5 A6
• No. of positions where split can occur = 2.
Therefore, k = (1, 2), (2, 3) (3, 4), (4, 5) respectively.
• Number of different parenthesizations:
A1 A2 A3 :
m [1, 1] + m [2, 3] + p0 p1 p3 = 0 + 2625 + 30 x 35 x 05 = 7,875
m [1, 2] + m [3, 3] + p0 p2 p3 = 15750 + 0 + 30 x 15 x 05 = 18,000
s [1, 3] = 1
A2 A3 A4 :
m [2, 2] + m [3, 4] + p1 p2 p4 = 0 + 750 + 30 x 15 x 10 = 6,000
m [2, 3] + m [4, 4] + p1 p3 p4 = 2625 + 0 + 35 x 05 x 10 = 4,375
s [2, 4] = 3
m [1, 3] = min
= 4,375m [2, 4] = min
= 7,875

19. Example…
A3 A4 A5 :
m [3, 3] + m [4, 5] + p2 p3 p5 = 0 + 1000 + 15 x 05 x 20 = 2,500
m [3, 4] + m [5, 5] + p2 p4 p5 = 750 + 0 + 15 x 10 x 20 = 3,750
s [3, 5] = 3
A4 A5 A6 :
m [4, 4] + m [5, 6] + p3 p4 p6 = 0 + 5000 + 05 x 10 x 25 = 6,250
m [4, 5] + m [6, 6] + p3 p5 p6 = 1000 + 0 + 05 x 20 x 25 = 3,500
s [4, 6] = 5
m [3, 5] = min
= 3,500m [4, 6] = min
= 2,500

20. Example…
n = 6; pi = 30, 35, 15, 5, 10, 20, 25; l = 3 i = 1 to n - l + 1; j = i + l – 1; k = i to j – 1
q = m [i, k] + m [k + 1, j] + pi-1 pk pj
i = 1
j = 1+3-1 = 3
i = 2
j = 2+3-1 = 4
k = 1
q=m[1,1]+m[2,3]+ p0 p1 p3
=0+2625+30x35x5
q = 7,875
k = 2
q=m[1,2]+m[3,3]+ p0 p2 p3
=15750+0+30x15x5
q = 18,000
k = 2
q=m[2,2]+m[3,4]+ p1 p2 p4
=0+750+35x15x10
q = 6,000
k = 3
q=m[2,3]+m[4,4]+ p1 p3 p4
=2625+0+35x5x10
q = 4,375
m [1, 3] = min (7875, 18000) = 7,875
s [1, 3] = 1
m [2, 4] = min (6000, 4375) = 4,375
s [2,4] = 3
i = 3
j = 3+3-1 = 5
i = 4
j = 4+3-1 = 6
k = 3
q=m[3,3]+m[4,5]+ p2 p3 p5
=0+1000+15x5x20
q = 2,500
k = 4
q=m[3,4]+m[5,5]+ p2 p4 p5
=750+0+15x10x20
q = 3,750
k = 4
q=m[4,4]+m[5,6]+ p3 p4 p6
=0+5000+5x10x25
q = 6,250
k = 5
q=m[4,5]+m[6,6]+ p3 p5 p6
=1000+0+5x20x25
q = 3,500
m [3, 5] = min (2500, 3750) = 2,500
s [3, 5] = 3
m [4, 6] = min (6250, 3500) = 3,500
s [4, 6] = 5

21. Example…
1 2 3 4 5 6
1 0 15,750 7,875
2 0 2,625 4,375
3 0 750 2,500
4 0 1,000 3,500
5 0 5,000
6 0
j
i
Table m 1 2 3 4 5 6
1 1 1
2 2 3
3 3 3
4 4 5
5 5
Table s
j
i

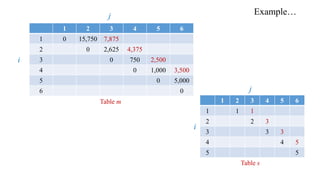
22. Example…
• l = 4 → 4 Matrices
• Matrices: A1 A2 A3 A4, A2 A3 A4 A5, A3 A4 A5 A6
• No. of positions where split can occur = 3.
Therefore, k = (1, 2, 3), (2, 3, 4) (3, 4, 5) respectively.
• Number of different parenthesizations:
A1 A2 A3 A4 :
m [1, 1] + m [2, 4] + p0 p1 p4 = 0 + 4375 + 30 x 35 x 10 = 14,875
m [1, 4] = min m [1, 2] + m [3, 4] + p0 p2 p4 = 15750 + 750 + 30 x 15 x 10 = 21,000 = 9,375
m [1, 3] + m [4, 4] + p0 p3 p4 = 7875 + 0 + 30 x 5 x 10 = 9,375
s [1, 4] = 1

23. Example…
A2 A3 A4 A5 :
m [2, 2] + m [3, 5] + p1 p2 p5 = 0 + 2500 + 35 x 15 x 20 = 13,000
m [2, 5] = min m [2, 3] + m [4, 5] + p1 p3 p5 = 2625 + 1000 + 35 x 5 x 20 = 7,125 = 7,125
m [2, 4] + m [5, 5] + p1 p4 p5 = 4375 + 0 + 30 x 10 x 20 = 11,375
s [2, 5] = 3
A3 A4 A5 A6 :
m [3, 3] + m [4, 6] + p2 p3 p6 = 0 + 3500 + 15 x 5 x 25 = 5,375
m [3, 6] = min m [3, 4] + m [5, 6] + p2 p4 p6 = 750 + 3500 + 15 x 10 x 25 = 8,000 = 5,375
m [3, 5] + m [6, 6] + p2 p5 p6 = 2500 + 0 + 15 x 20 x 25 = 10,000
s [3, 6] = 3

24. Example…
n = 6; pi = 30, 35, 15, 5, 10, 20, 25; l = 4 i = 1 to n - l + 1; j = i + l – 1; k = i to j – 1
q = m [i, k] + m [k + 1, j] + pi-1 pk pj
i = 1; j = 1+4-1 = 4
k = 1
q=m[1,1]+m[2,4]+ p0 p1 p4
=0+4375+30x35x10 = 14,875
k = 2
q=m[1,2]+m[3,4]+ p0 p2 p4
=15750+750+30x15x10 = 21,000
k = 3
q=m[1,3]+m[4,4]+ p0 p3 p4
=7875+0+30x5x10 = 9,375
m [1, 4] = min (14875, 21000, 9375) = 9,375; s [1, 4] = 3
i = 2; j = 2+4-1 = 5
k = 2
q=m[2,2]+m[3,5]+ p1 p2 p5
=0+2500+35x15x20 = 13,000
k = 3
q=m[2,3]+m[4,5]+ p1 p3 p5
=2625+1000+35x5x20 = 7,125
k = 4
q=m[2,4]+m[5,5]+ p1 p4 p5
=4375+0+35x10x20 = 11,375
m [2, 5] = min (13000, 7125, 11375) = 7,125; s [2, 5] = 3
i = 3; j = 3+4-1 = 6
k = 3
q=m[3,3]+m[4,6]+ p2 p3 p6
=0+3500+15x5x25 = 5,375
k = 4
q=m[3,4]+m[5,6]+ p2 p4 p6
=750+3500+15x10x25 = 8,000
k = 5
q=m[3,5]+m[6,6]+ p2 p5 p6
=2500+0+15x20x25 = 10,000
m [3, 6] = min (5375, 8000, 10000) = 5,375; s [3, 6] = 3

25. Example…
1 2 3 4 5 6
1 0 15,750 7,875 9,375
2 0 2,625 4,375 7,125
3 0 750 2,500 5,375
4 0 1,000 3,500
5 0 5,000
6 0
j
i
Table m 1 2 3 4 5 6
1 1 1 3
2 2 3 3
3 3 3 3
4 4 5
5 5
Table s
j
i

26. Example…
• l = 5 → 5 Matrices
• Matrices: A1 A2 A3 A4 A5, A2 A3 A4 A5 A6
• No. of positions where split can occur = 4.
Therefore, k = (1, 2, 3, 4), (2, 3, 4, 5) respectively.
• Number of different parenthesizations:
A1 A2 A3 A4 A5 :
m [1, 1] + m [2, 5] + p0 p1 p5 = 0 + 7175 + 30 x 35 x 20 = 28,125
m [1, 2] + m [3, 5] + p0 p2 p5 = 15750 + 2500 + 30 x 15 x 20 = 27,250
m [1, 3] + m [4, 5] + p0 p3 p5 = 7875 + 1000 + 30 x 5 x 20 = 11,875
m [1, 4] + m [5, 5] + p0 p4 p5 = 9375 + 0 + 35 x 10 x 20 = 16,375
s [1, 5] = 3
A2 A3 A4 A5 A6 :
m [2, 2] + m [3, 6] + p1 p2 p6 = 0 + 5375 + 35 x 15 x 25 = 18,500
m [2, 3] + m [4, 6] + p2 p3 p6 = 2625 + 3500 + 15 x 5 x 25 = 8,000
m [2, 4] + m [5, 6] + p1 p4 p6 = 4375 + 5000 + 35 x 10 x 25 = 18,125
m [2, 5] + m [6, 6] + p1 p5 p6 = 7125 + 0 + 35 x 20 x 25 = 24,625
s [2, 6] = 3
m [1, 5] = min = 11,875
m [2, 6] = min = 8,000

27. Example…
n = 6; pi = 30, 35, 15, 5, 10, 20, 25; l = 5 i = 1 to n - l + 1; j = i + l – 1; k = i to j – 1
q = m [i, k] + m [k + 1, j] + pi-1 pk pj
i = 1
j = 1+5-1 = 5
k = 1
q=m[1,1]+m[2,5]+ p0 p1 p5
=0+7125+30x35x20
q = 28,125
k = 2
q=m[1,2]+m[3,5]+ p0 p2 p5
=15750+2500+30x15x20
q = 27,250
k = 3
q=m[1,3]+m[4,5]+ p0 p3 p5
=7875+1000+30x5x20
q = 11,875
k = 4
q=m[1,4]+m[5,5]+ p0 p4 p5
=9375+0+35x10x20
q = 16,375
m [1, 5] = min (28125, 27250, 11875, 16375) = 11,875
s [1, 5] = 3
i = 2
j = 2+5-1 = 6
k = 2
q=m[2,2]+m[3,6]+ p1 p2 p6
=0+5375+35x15x25
q = 18,500
k = 3
q=m[2,3]+m[4,6]+ p2 p3 p6
=2625+3500+15x5x25
q = 8,000
k = 4
q=m[2,4]+m[5,6]+ p1 p4 p6
=4375+5000+35x10x25
q = 18,125
k = 5
q=m[2,5]+m[6,6]+ p1 p5 p6
=7125+0+35x20x25
q = 24,625
m [2, 6] = min (18500, 8000, 18125, 24625) = 8,000
s [2, 6] = 3

28. Example…
1 2 3 4 5 6
1 0 15,750 7,875 9,375 11,875
2 0 2,625 4,375 7,125 8,000
3 0 750 2,500 5,375
4 0 1,000 3,500
5 0 5,000
6 0
j
i
Table m 1 2 3 4 5 6
1 1 1 3 3
2 2 3 3 3
3 3 3 3
4 4 5
5 5
Table s
j
i

29. Example…
• l = 6 → 6 Matrices
• Matrices: A1 A2 A3 A4 A5 A6
• No. of positions where split can occur = 5.
Therefore, k = (1, 2, 3, 4, 5).
• Number of different parenthesizations:
A1 A2 A3 A4 A5 :
m [1, 1] + m [2, 6] + p0 p1 p6 = 0 + 8000 + 30 x 35 x 25 = 34,250
m [1, 2] + m [3, 6] + p0 p2 p6 = 15750 + 5375 + 35 x 15 x 25 = 32,375
m [1, 6] = min m [1, 3] + m [4, 6] + p0 p3 p6 = 7875 + 3500 + 30 x 5 x 25 = 15,125 = 15,125
m [1, 4] + m [5, 6] + p0 p4 p6 = 9375 + 5000 + 35 x 10 x 25 = 21,875
m [1, 5] + m [6, 6] + p0 p5 p6 = 11875 + 0 + 35 x 20 x 25 = 26,875
s [1, 6] = 3

30. Example…
n = 6; pi = 30, 35, 15, 5, 10, 20, 25; l = 6 i = 1 to n - l + 1; j = i + l – 1; k = i to j – 1
q = m [i, k] + m [k + 1, j] + pi-1 pk pj
i = 1
j = 1+6-1 = 6
k = 1
q = m [1,1] + m [2,6] + p0 p1 p6
= 0+8000+30x35x25= 34,250
k = 2
q = m [1,2] + m [3,6] + p0 p2 p6
=15750+5375+30x15x25= 32,375
k = 3
q = m [1,3] + m [4,6] + p0 p3 p6
=7875+3500+30x5x25= 15,125
k = 4
q = m [1,4] + m [5,6] + p0 p4 p6
=9375+5000+30x10x25= 21,875
k = 5
q = m [1,5] + m [6,6] + p0 p5 p6
=11875+0+30x20x25 = 26,875
m [1, 6] = min (34250, 34250, 15125, 21875, 26875) = 15125
s [1, 6] = 3

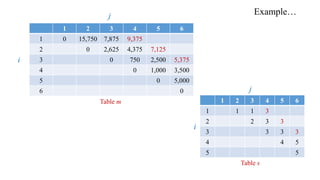
31. Example…
1 2 3 4 5 6
1 0 15,750 7,875 9,375 11,875 15125
2 0 2,625 4,375 7,125 8,000
3 0 750 2,500 5,375
4 0 1,000 3,500
5 0 5,000
6 0
j
i
Table m 1 2 3 4 5 6
1 1 1 3 3 3
2 2 3 3 3
3 3 3 3
4 4 5
5 5
Table s
j
i
The Minimum number of Scalar
Multiplications to multiply the 6
matrices A1 A2 A3 A4 A5 A6 is:
m [1, 6] = 15,125.
The Optimal split occurs at:
s [1, 6] = 3.

32. • Optimal way of computing A 1 . . n is: A 1 . . S [1, n] x A S [1, n] + 1 . . n
• The initial call PRINT-OPTIMAL-PARENS (s, 1, n) prints an optimal
parenthesization of A1, A2, . . . , An
PRINT-OPTIMAL-PARENS (s, i, j)
If (i == j)
Print “A”i
Else Print “(”
PRINT-OPTIMAL-PARENS (s, i, s [i, j])
PRINT-OPTIMAL-PARENS (s, s [i, j] + 1, j )
Print “)”
4. Constructing an Optimal Solution
PRINT-OPTIMAL-PARENS (s, 1, 6)
prints the Parenthesization:
((A1 (A2 A3)) ((A4 A5) A6))

33. PRINT-OPTIMAL-PARENS (s, 1, 6) Push (i = 1, j = 6)
(
PRINT-OPTIMAL-PARENS (s, 1, 3) Push (i = 1, j = 3)
((
PRINT-OPTIMAL-PARENS (s, 1, 1) Push (i = 1, j = 1)
((A1 Pop (i = 1, j = 1)
PRINT-OPTIMAL-PARENS (s, 2, 3) Push (i = 2, j = 3)
((A1(
PRINT-OPTIMAL-PARENS (s, 2, 2) Push (i = 2, j = 2)
((A1(A2 Pop (i = 2, j = 2)
PRINT-OPTIMAL-PARENS (s, 3, 3) Push (i = 3, j = 3)
((A1(A2A3 Pop (i = 3, j = 3)
((A1(A2A3) Pop (i = 2, j = 3)
Constructing an Optimal Solution…

34. ((A1(A2A3)) Pop (i = 1, j = 3)
PRINT-OPTIMAL-PARENS (s, 4, 6) Push (i = 4, j = 6)
((A1(A2A3))(
PRINT-OPTIMAL-PARENS (s, 4, 5) Push (i = 4, j = 5)
((A1(A2A3))((
PRINT-OPTIMAL-PARENS (s, 4, 4) Push (i = 4, j = 4)
((A1(A2A3))((A4 Pop (i = 4, j = 4)
PRINT-OPTIMAL-PARENS (s, 5, 5) Push (i = 5, j = 5)
((A1(A2A3))((A4A5 Pop (i = 5, j = 5)
((A1(A2A3))((A4A5) Pop (i = 4, j = 5)
PRINT-OPTIMAL-PARENS (s, 6, 6) Push (i = 6, j = 6)
((A1(A2A3))((A4A5)A6 Push (i = 6, j = 6)
((A1(A2A3))((A4A5)A6) Pop (i = 4, j = 6)
((A1(A2A3))((A4A5)A6)) Pop (i = 1, j = 6)
Optimal Parenthesization : ((A1(A2A3))((A4A5)A6))
Constructing an Optimal Solution…

35. References:
• Thomas H Cormen. Charles E Leiserson, Ronald L Rivest, Clifford Stein,
Introduction to Algorithms, Third Edition, The MIT Press Cambridge,
Massachusetts London, England.