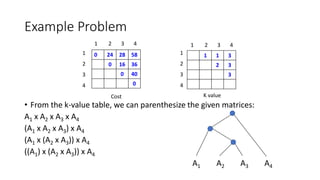
The document discusses dynamic programming with a focus on matrix chain multiplication as an optimization problem. It explains how to efficiently determine the sequence of matrix multiplications required to minimize the total number of operations, emphasizing the importance of subproblem optimality and overlap. Additionally, it outlines a dynamic programming algorithm that computes the optimal parenthesization bottom-up, resulting in a time complexity of O(n^3).










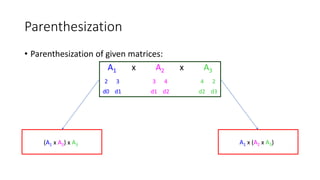
![Parenthesization
(A1 x A2) x A3
2 3 3 4 4 2
Number of Operations: C[1, 2] = 2 x 3 x 4 = 24 C[3, 3] = 0
New Dimension: 2 x 4 4 x 2
Number of Operations: 2 x 4 x 2 = 16
Total Number of operations: 24 + 16 = 40 Multiplications
General Notation for this operation: C[1, 2] + C[3, 3] + d0 + d2 + d3 = 40 ------------------------------ (i)](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-13-320.jpg)

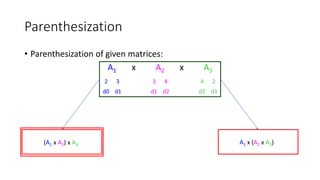
![Paranthesization
A1 x (A2 x A3)
2 3 3 4 4 2
Number of Operations: C[1, 1] = 0 C[2, 3] = 3 x 4 x 2 = 24
New Dimension: 2 x 3 3 x 2
Number of Operations: 2 x 3 x 2 = 12
Total Number of operations: 24 + 12 = 38 Multiplications
General Notation for this operation: C[1, 1] + C[2, 3] + d0 + d1 + d3 = 38 ------------------------------ (ii)](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-15-320.jpg)
![Parenthesization
• From Equation (i) and (ii):
C[1, 2] + C[3, 3] + d0 + d2 + d3 = 40 C[1, 1] + C[2, 3] + d0 + d1 + d3 = 38
>](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-16-320.jpg)
![Parenthesization
• From Equation (i) and (ii):
C[1, 2] + C[3, 3] + d0 + d2 + d3 = 40 C[1, 1] + C[2, 3] + d0 + d1 + d3 = 38
>
This is the optimal solution among the two ways](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-17-320.jpg)
![Parenthesization
• From Equation (i) and (ii), we can derive the generalized form
C[1, 2] + C[3, 3] + d0 + d2 + d3 = 40 C[1, 1] + C[2, 3] + d0 + d1 + d3 = 38
>
C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-18-320.jpg)



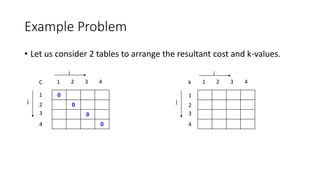
![Example Problem
• Let us find the C[1, 2]: C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j
C[1, 2] = min { C[1, 1] + C[2, 2] + d0 x d1 x d2}
1 ≤ 1< 2
K = 1
= 0 + 0 + 3 x 2 x 4
= 24
0 24
0
0
0
1
Cost K value
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-23-320.jpg)
![Example Problem
• Let us find the C[2, 3]: C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j
C[2, 3] = min { C[2, 2] + C[3, 3] + d1 x d2 x d3}
2 ≤ 2< 3
K = 2
= 0 + 0 + 2 x 4 x 2
= 16
0 24
0 16
0
0
1
2
Cost K value
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-24-320.jpg)
![Example Problem
• Let us find the C[3, 4]: C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j
C[3, 4] = min { C[3, 3] + C[4, 4] + d2 x d3 x d4}
3 ≤ 3< 4
K = 3
= 0 + 0 + 4 x 2 x 5
= 40
0 24
0 16
0 40
0
1
2
3
Cost K value
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-25-320.jpg)
![Example Problem
• Let us find the C[1, 3]: C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j
C[1, 3] = min C[1, 1] + C[2, 3] + d0 x d1 x d3 = 0 + 16 + 3 x 2 x 2 = 28
C[1, 2] + C[3, 3] + d0 x d2 x d3 = 24 + 0 + 3 x 4 x 2 = 48 When, K = 2
0 24 28
0 16
0 40
0
1 1
2
3
Cost K value
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4
When, K = 1
1 ≤ k < 3](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-26-320.jpg)
![Example Problem
• Let us find the C[2, 4]: C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j
C[2, 4] = min C[2, 2] + C[3, 4] + d1 x d2 x d4 = 0 + 40 + 2 x 4 x 5 = 80
C[2, 3] + C[4, 4] + d1 x d3 x d4 = 16 + 0 + 2 x 2 x 5 = 36 When, K = 3
0 24 28
0 16 36
0 40
0
1 1
2 3
3
Cost K value
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4
When, K = 2
2 ≤ k < 4](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-27-320.jpg)
![Example Problem
• Let us find the C[1, 4]: C[i, j] = min { C[i, k] + C[k + 1, j] + di-1 x dk x dj}
I ≤ k < j
C[1, 4] = min C[1, 1] + C[2, 4] + d0 x d1 x d4 = 0 + 36 + 3 x 2 x 5 =66
C[1, 2] + C[3, 4] + d0 x d2 x d4 = 24 + 40 + 3 x 4 x 5 = 124
C[1, 3] + C[4, 4] + d0 x d3 x d4 = 28 + 0 + 3 x 2 x 5 = 58
When, K = 2
0 24 28 58
0 16 36
0 40
0
1 1 3
2 3
3
Cost K value
1 2 3 4 1 2 3 4
1
2
3
4
1
2
3
4
When, K = 1
When, K = 3
1 ≤ k < 4](https://image.slidesharecdn.com/dynamicprogrammingmatrixchainmultiplication-231116130947-9e7ce173/85/Dynamic-Programming-Matrix-Chain-Multiplication-28-320.jpg)