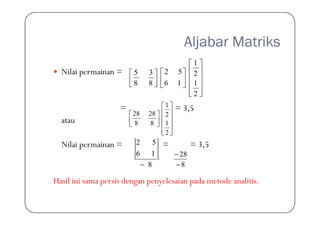
Metode aljabar matriks digunakan untuk menyelesaikan permainan 2x2 dengan mencari strategi optimal pemain dan nilai permainan. Matriks permainan dibentuk dan strategi optimal didapat dari adjoint dan cofactor matriks. Contoh perhitungan menunjukkan strategi campuran optimal sama dengan hasil metode analitis dan nilai permainannya adalah 3,5.

![Aljabar Matriks
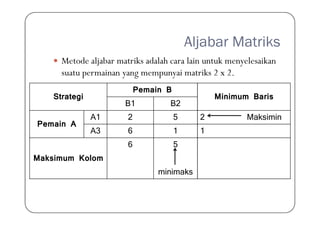
Dari tabel permainan 2 x 2 dengan strategi campuran
tersebut, maka bentuk matriksnya adalah:
B1 B2
A1
A3
[ ]ijP=
16
52
A3
Dimana Pij menunjukkan jumlah payoff dalam baris ke i dan
kolom ke j.
Strategi-strategi optimal untuk perusahaan A dan B serta nilai
permainannya dapat dicari dengan formula sebagai berikut:
[ ]ij
16](https://image.slidesharecdn.com/metodealjabarmatriks-130503102554-phpapp01/85/Metode-aljabar-matriks-3-320.jpg)
![Aljabar Matriks
Strategi optimal perusahaan A =
Strategi optimal perusahaan B =
[ ]
[ ]
1
1
][11
][11
adj
adj
P
P
[ ] ][11 cofP
Strategi optimal perusahaan B =
Nilai permainan = [Strategi optimal A] [Pij] [Strategi optimal B]
=
[ ]
[ ]
1
1
][11
][11
adj
cof
P
P
[ ]
1
1
][11
][
adj
ij
P
P](https://image.slidesharecdn.com/metodealjabarmatriks-130503102554-phpapp01/85/Metode-aljabar-matriks-4-320.jpg)
![Aljabar Matriks
Padj = adjoint matrix
Pcof = cofactor matrix
[Pij] = matriks permainan
[Pij] = determinan matriks permainan
Dalam persamaan ini, strategi optimal A ada dalam vektorDalam persamaan ini, strategi optimal A ada dalam vektor
baris, dan strategi optimal B diletakkan dalam vektor kolom.
[Pij] = Pcof =
Padj = [Pcof]T = [Pij] = = 2-30 = -28
16
52
−
−
25
61
−
−
26
51
16
52](https://image.slidesharecdn.com/metodealjabarmatriks-130503102554-phpapp01/85/Metode-aljabar-matriks-5-320.jpg)
![Aljabar Matriks
Strategi optimal A = =
[ ]
[ ]
−
−
−
−
1
1
26
51
11
26
51
11
[ ]
8
35
−
−
− 61
Strategi optimal B = =
Jadi strategi-strategi campuran yang optimal =
A1 = A3 = B1 = B2 =
[ ]
[ ]
−
−
−
−
1
1
26
51
11
25
61
11
[ ]
8
44
−
−−
8
5
8
3
2
1
8
4
=
2
1
8
4
=](https://image.slidesharecdn.com/metodealjabarmatriks-130503102554-phpapp01/85/Metode-aljabar-matriks-6-320.jpg)