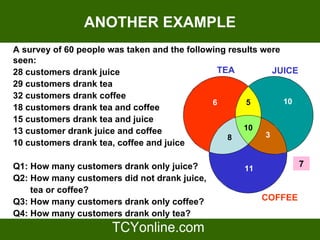
The document explains the concept of sets, defining them as collections of distinct, unordered elements. It distinguishes between finite and infinite sets, introduces the idea of equality between sets, and discusses the universal set. Additionally, it covers operations on sets, including union and intersection, and provides examples using Venn diagrams.

1. SETS

2. "Set" is synonymous with the words: "collection", "aggregate", "class" and is comprised of elements/objects/members. The following are some examples of sets: The collection of vowels in English Alphabets. The collection of all past Presidents of the Indian Union. The weights of all the students of a class. SET

3. DEFINING A SET A set is a collection of well defined entities, objects or elements. OR A set is a group of one or more elements with common characteristics. OR A set is a collection of distinct, unordered objects. Sets are typically collection of numbers. So, a set may contain any type of data (including other sets).

4. A set is described by listing elements, separated by commas, within brackets. For example: A set of vowels of English Alphabet may be described as: {a, e, i, o, u} A set of even natural numbers can be described as: {2, 4, 6, 8,…} Note: The order in which the elements are written makes no difference. Also, repetition of an element has no effect. For example {1, 2, 3, 2} is the same set as {1, 2, 3}. DESCRIBING A SET

5. Finite set: A set is called a finite set, if its elements can be counted and the process of counting terminates at a certain natural number say, ‘n’. Example: {1, 2, 3, 4, 5} , {1, 2, 3, 4,………..up to 100} Infinite Set: A set which is not finite or in other words, a set in which the process of counting does not terminate is an infinite set. Example: Set of natural numbers, or {2, 4, 6, 8, 10,…………………. } set of even numbers or {1, 3, 5, 7, 9,……………………} set of odd numbers FINITE AND INFINITE SETS

6. Two sets A and B are said to be equal, if every element of A is a member of B, and every element of B is a member of A. If sets A and B are equal, we write A = B . Similarly, Unequal sets: When they are not equal or there exists at least one distinct element between these two sets. We write: A  B, when A and B are not equal. Let A = {1, 2, 5, 6} and B = {5, 6, 2, 1}. Then A = B because each element of A is an element of B and vice – versa. EQUAL SETS

7. There happens to be a set ‘U’ that contains all the elements under consideration. Such a set is called the universal set. For example : A = {1, 2, 3, 4, 5), B = {4, 5, 6, 7, 8, 9 }. We can say that they are both contained in their universal set, which is a set of natural numbers. In plane geometry, the set of all points in the plane is the universal set. UNIVERSAL SET

8. MORE EXAMPLE Given that U = {4, 5, 6, 7, 8, 9, 10, 11, 12} universal set, list the elements of the following sets. a) A = { x : x is a factor of 72} b) B = { x : x is a prime number} c) C = {x : x is a odd number } Solution: The elements of sets A and B can only be selected from the given universal set U. a) A = {4, 6, 8, 9, 12} b) B = {5, 7, 11} c) C = {5, 7, 9, 11}

9. Often pictures are very helpful in our thinking. In set theory we use closed curves (usually circles) and rectangles to represent sets and a combination of these is named as Venn-diagrams . Below are some examples of Venn-diagrams: U = universal set A = subset of U (i.e. A is contained in U) A’ = complement of A (i.e. all the elements of U that are not included in A) VENN DIAGRAMS A’ U A

10. EXAMPLE

11. Universal set with 2 disjoint sets A & B U = real numbers A = odd numbers B = even numbers Universal set with two intersecting sets A & B U = real numbers A = even numbers B = number divisible by 5 VENN DIAGRAMS A U B A U B

12. Set A and subset B A = real numbers B = even numbers B = boys in the school T = tennis players G = Girls in the school C = boys who play cricket T = boys who play tennis G = boys who play golf C T G VENN DIAGRAMS A B B T G

13. Union: Let A and B be two sets. The union of A and B is the set of all those elements, which belong to either set A or set B or to both A and B. We shall use the notation: A  B (read as "A union B") to denote the union of A and B. Intersection: Let A and B be two sets. The intersection of A and B is the set of only those elements that belong to both A and B. We shall use the notation A  B (read as "A intersection B") A B A B OPERATIONS ON SETS

14. Cardinal Number ‘n’ Where n (A) means number of elements in set A whereas in this diagram->> n (A  B) = n (A) + n (B) – n (A  B) The last term has to be subtracted because it has been counted twice, once in n(A) and again in n (B). USE OF VENN DIAGRAMS A B So, In this Venn Diagram n (A  B) = n (A) + n (B) U A B

15. Only B Only A & B Only C Only A & C Only A Only B & C A & B and C only CONSIDER THREE SETS A, B AND C

16. Ex. In a group of 1000 persons, 760 can speak Hindi & 430 can speak Bengali. Find how many can speak both? Sol. Let H denote Hindi, B denote Bengali Alternative Method: We have a + b = 760, b + c = 430, a + b + c = 1000  a = 570, c = 240 or b = 190 or 190 people can speak both. n (H  B) = n(H) + n(B) – (H  B)  1000 = 760 + 430 – n (H  B)  n(H  B)= 190 EXAMPLE B H a b c

17. A survey of 60 people was taken and the following results were seen: 28 customers drank juice 29 customers drank tea 32 customers drank coffee 18 customers drank tea and coffee 15 customers drank tea and juice 13 customer drank juice and coffee 10 customers drank tea, coffee and juice Q1: How many customers drank only juice? Q2: How many customers did not drank juice, tea or coffee? Q3: How many customers drank only coffee? Q4: How many customers drank only tea? JUICE COFFEE 10 5 8 3 10 6 11 7 ANOTHER EXAMPLE TEA