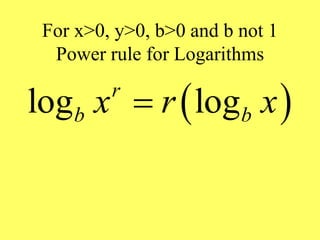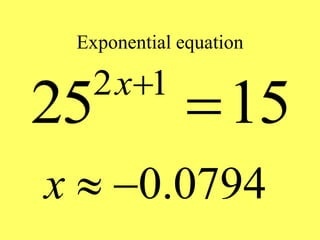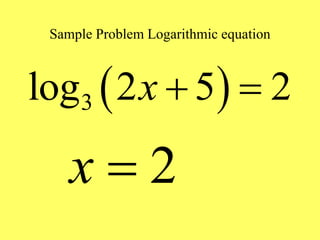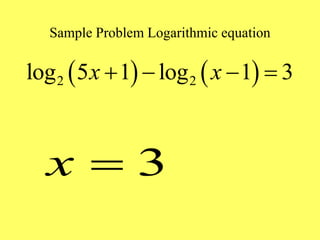This document provides an overview of exponential and logarithmic functions covered in Chapter 9 of an Intermediate Algebra textbook. It defines exponential, logarithmic, and inverse functions and covers their graphs and properties. It discusses the bases e and 10 and how to evaluate logarithmic expressions. It also addresses how to solve exponential and logarithmic equations. The objectives are to work with these function types and understand their relationships and applications.

1. Intermediate Algebra
Chapter 9
•Exponential
•and
•Logarithmic
Functions

2. Intermediate Algebra 9.1-9.2
•Review of Functions

3. Def: Relation
• A relation is a set of ordered pairs.
• Designated by:
• Listing
• Graphs
• Tables
• Algebraic equation
• Picture
• Sentence

4. Def: Function
• A function is a set of ordered pairs
in which no two different ordered
pairs have the same first
component.
• Vertical line test – used to
determine whether a graph
represents a function.

5. Defs: domain and range
• Domain: The set of first
components of a relation.
• Range: The set of second
components of a relation

6. Examples of Relations:
    
 
1,2 , 3,4 5,6
     
 
1,2 , 3,2 , 5,2
     
 
1,2 , 1,4 , 1,6

7. Objectives
• Determine the domain, range of
relations.
• Determine if relation is a
function.

8. Intermediate Algebra 9.2
•Inverse Functions

9. Inverse of a function
• The inverse of a function is determined by
interchanging the domain and the range of
the original function.
• The inverse of a function is not necessarily
a function.
• Designated by
• and read f inverse
1
f 
1
f 

10. One-to-One function
• Def: A function is a one-to-one
function if no two different
ordered pairs have the same
second coordinate.

11. Horizontal Line Test
• A function is a one-to-one
function if and only if no
horizontal line intersects the
graph of the function at more
than one point.

12. Inverse of a function
     
 
1,2 , 3,4 , 5,6
f 
    
 
1
2,1 4,3 , 6,5
f 


13. Inverse of function
     
 
1,2 , 3,2 , 5,2
f 
     
 
1
2,1 , 2,3 , 2,5
f 


14. Objectives:
• Determine the inverse of a function whose
ordered pairs are listed.
• Determine if a function is one to one.

15. Intermediate Algebra 9.3
•Exponential Functions

16. Michael Crichton – The Andromeda Strain
(1971)
• The mathematics of uncontrolled
growth are frightening. A single cell of
the bacterium E. coli would, under
ideal circumstances, divide every
twenty minutes. It this way it can be
shown that in a single day, one cell of
E. coli could produce a super-colony
equal in size and weight to the entire
planet Earth.”

17. Definition of Exponential
Function
• If b>0 and b not equal to 1 and x is any real
number, an exponential function is written
as

log log
log log
1
1
b b
b b
x
x
x y
y
xy x y
e
x

 


 
 
  
 
 
( ) x
f x b


18. Graphs-Determine domain,
range, function, 1-1, x intercepts,
y intercepts, asymptotes
( ) 2x
f x 

19. Graphs-Determine domain,
range, function, 1-1, x intercepts,
y intercepts, asymptotes
1
( )
2
x
g x
 
  
 

20. Growth and Decay
•Growth: if b > 1
•Decay: if 0 < b < 1
( ) x
f x b


21. Properties of graphs of
exponential functions
• Function and 1 to 1
• y intercept is (0,1) and no x intercept(s)
• Domain is all real numbers
• Range is {y|y>0}
• Graph approaches but does not touch x
axis – x axis is asymptote
• Growth or decay determined by base

22. Natural Base e
1
1
x
as x e
x
 
   
 
 
2.718281828
e 

23. Calculator Keys
• Second function of divide
• Second function of LN (left
side)
x
e

24. Property of equivalent exponents
• For b>0 and b not equal to 1
x y
if b b
then x y



25. Compound Interest
• A= amount P = Principal t = time
• r = rate per year
• n = number of times compounded
1
nt
r
A P
n
 
 
 
 

26. Compound interest problem
• Find the accumulated amount in an account
if $5,000 is deposited at 6% compounded
quarterly for 10 years.
 
4 10
.06
5000 1
4
A
 
 
 
 
$9070.09
A 

27. Objectives:
• Determine and graph
exponential functions.
• Use the natural base e
• Use the compound interest
formula.

28. Dwight Eisenhower – American
President
•“Pessimism never
won any battle.”

29. Intermediate Algebra 9.4,9.5,9.6
•Logarithmic Functions

30. Definition: Logarithmic Function
• For x > 0, b > 0 and b not equal to 1 toe
logarithm of x with base b is defined by the
following:
log y
b x y x b
  

31. Properties of Logarithmic Function
• Domain:{x|x>0}
• Range: all real numbers
• x intercept: (1,0)
• No y intercept
• Approaches y axis as vertical
asymptote
• Base determines shape.

32. Shape of logarithmic graphs
• For b > 1, the graph rises from
left to right.
• For 0 < b < 1, the graphs falls
from left to right.

33. Common Logarithmic Function
The logarithmic function with
base 10
10
log log
x y x y
  

34. Natural logarithmic function
The logarithmic function with a
base of e
log ln
e x y x y
  

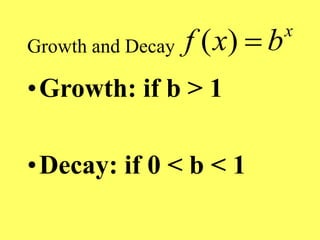
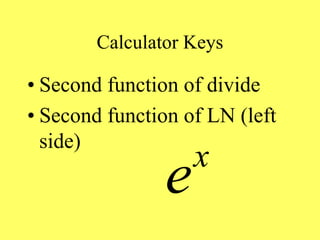
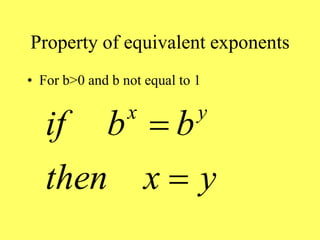
35. Calculator Keys
•[LOG]
•[LN]

36. Objective:
• Determine the common
log or natural log of any
number in the domain of
the logarithmic function.

37. Change of Base Formula
• For x > 0 for any positive bases a and b
log
log
log
a
b
a
x
x
b


38. Problem: change of base
3
log 5 10
10
log 5 log5
log 3 log3
 
log 5 ln5
log 3 ln3
e
e
 1.46


39. Objective
• Use the change of base
formula to determine an
approximation to the
logarithm of a number when
the base is not 10 or e.

40. Intermediate Algebra 10.5
•Properties
•of
•Logarithms

41. Basic Properties of logarithms
log 1 0
b 
log 1
b b 
log log
b b
x y x y
  

42. For x>0, y>0, b>0 and b not 1
Product rule of Logarithms
 
log log log
b b b
xy x y
 

43. For x>0, y>0, b>0 and b not 1
Quotient rule for Logarithms
log log log
b b b
x
x y
y
 
 
 
 

44. For x>0, y>0, b>0 and b not 1
Power rule for Logarithms
 
log log
r
b b
x r x


45. Objectives:
• Apply the product, quotient,
and power properties of
logarithms.
• Combine and Expand
logarithmic expressions

46. Theorems summary Logarithms:
 
.log log log
b b b
I xy x y
 
.log log log
b b b
x
II x y
y
 
 
 
 
 
.log log
r
b b
III x r x


47. Norman Vincent Peale
• “Believe it is possible to
solve your problem.
Tremendous things happen to
the believer. So believe the
answer will come. It will.”

48. Intermediate Algebra 9.7
•Exponential
•and
•Logarithmic
•Equations

49. Objective:
• Solve equations that have
variables as exponents.

50. Exponential equation
2 1
25 15
x

0.0794
x  

51. Objective:
•Solve equations
containing logarithms.

52. Sample Problem Logarithmic equation
 
3
log 2 5 2
x  
2
x 

53. Sample Problem Logarithmic equation
   
2 2
log 5 1 log 1 3
x x
   
3
x 

54. Sample Problem Logarithmic equation
 
2 2
log 2 log 3
x x
  
4 2
x or x
  
 
2

55. Sample Problem Logarithmic equation
 
5 5 5
log log 3 log 4
x x
  
 
1

56. Walt Disney
• “Disneyland will never be
completed. It will
continue to grow as long
as there is imagination
left in the world.”

58. Galileo Galilei (1564-1642)
•“The universe…is
written in the language
of mathematics…”