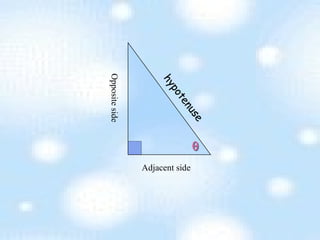
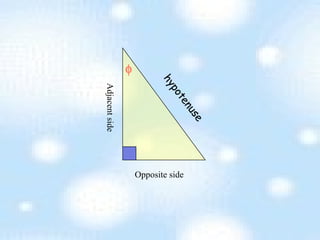
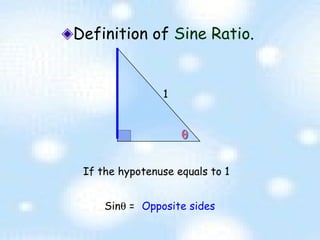
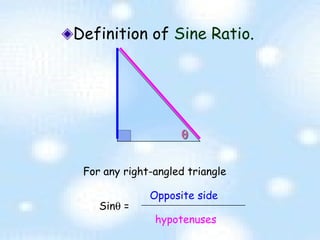
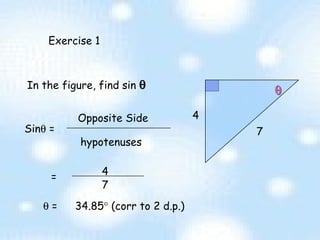
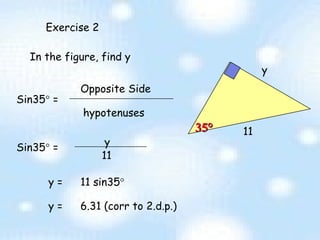
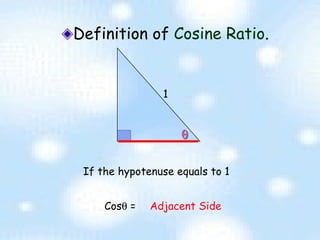
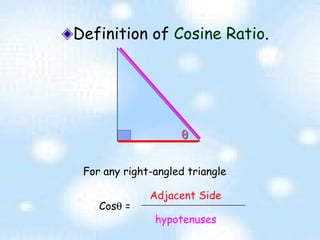
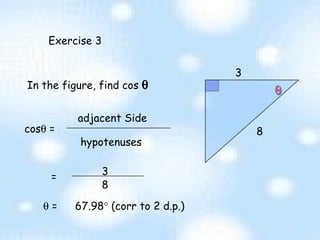
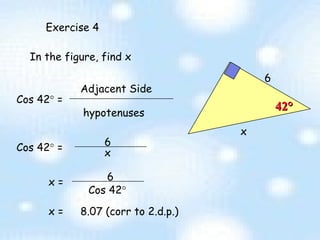
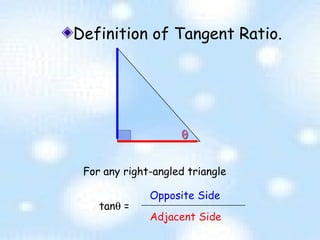
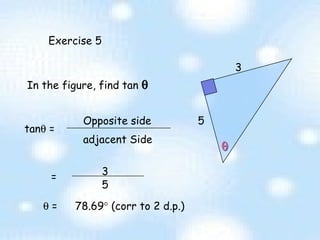
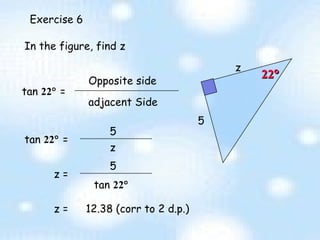
The document provides an introduction to trigonometry and trigonometric ratios. It defines the sine, cosine, and tangent ratios using right triangles and their adjacent, opposite, and hypotenuse sides. Examples are given to calculate sine, cosine, and tangent ratios based on values provided in various right triangles. Credit is given to three individuals for an accompanying PowerPoint presentation on this topic.

1. I would like to give credit to the following people below for the wonderful PowerPoint presentation. Thank you very much, Ms. Garcia Moy Yee Ping 3 Szeto Kwok Fai 2 Chau Ping 1

2. Trigonometry ( 三角幾何 ) means “ Triangle” and “Measurement” Introduction Trigonometric Ratios

3. Adjacent , Opposite Side and Hypotenuse of a Right Angle Triangle .

4. Adjacent side Opposite side hypotenuse 

5. hypotenuse Adjacent side Opposite side 

6. Three Types Trigonometric Ratios There are 3 kinds of trigonometric ratios we will learn. sine ratio cosine ratio tangent ratio

7. Sine Ratios Definition of Sine Ratio. Application of Sine Ratio.

8. Definition of Sine Ratio . 1 If the hypotenuse equals to 1 Sin  =  Opposite sides

9. Definition of Sine Ratio . For any right-angled triangle Sin  =  Opposite side hypotenuses

10. Exercise 1 In the figure, find sin  Sin  = Opposite Side hypotenuses = 4 7  = 34.85  (corr to 2 d.p.)  4 7

11. Exercise 2 11 In the figure, find y Sin35  = Opposite Side hypotenuses y 11 y = 6.31 (corr to 2.d.p.) 35 ° y Sin35  = y = 11 sin35 

12. Cosine Ratios Definition of Cosine. Relation of Cosine to the sides of right angle triangle.

13. Definition of Cosine Ratio . 1 If the hypotenuse equals to 1 Cos  =  Adjacent Side

14. Definition of Cosine Ratio . For any right-angled triangle Cos  =  hypotenuses Adjacent Side

15. Exercise 3  3 8 In the figure, find cos  cos  = adjacent Side hypotenuses = 3 8  = 67.98  (corr to 2 d.p.)

16. Exercise 4 6 In the figure, find x Cos 42  = Adjacent Side hypotenuses 6 x x = 8.07 (corr to 2.d.p.) 42 ° x Cos 42  = x = 6 Cos 42 

17. Tangent Ratios Definition of Tangent. Relation of Tangent to the sides of right angle triangle.

18. Definition of Tangent Ratio. For any right-angled triangle tan  =  Adjacent Side Opposite Side

19. Exercise 5  3 5 In the figure, find tan  tan  = adjacent Side Opposite side = 3 5  = 78.69  (corr to 2 d.p.)

20. Exercise 6 z 5 In the figure, find z tan 22  = adjacent Side Opposite side 5 z z = 12.38 (corr to 2 d.p.) 22  tan 22  = 5 tan 22  z =

21. Conclusion Make Sure that the triangle is right-angled

22. The END