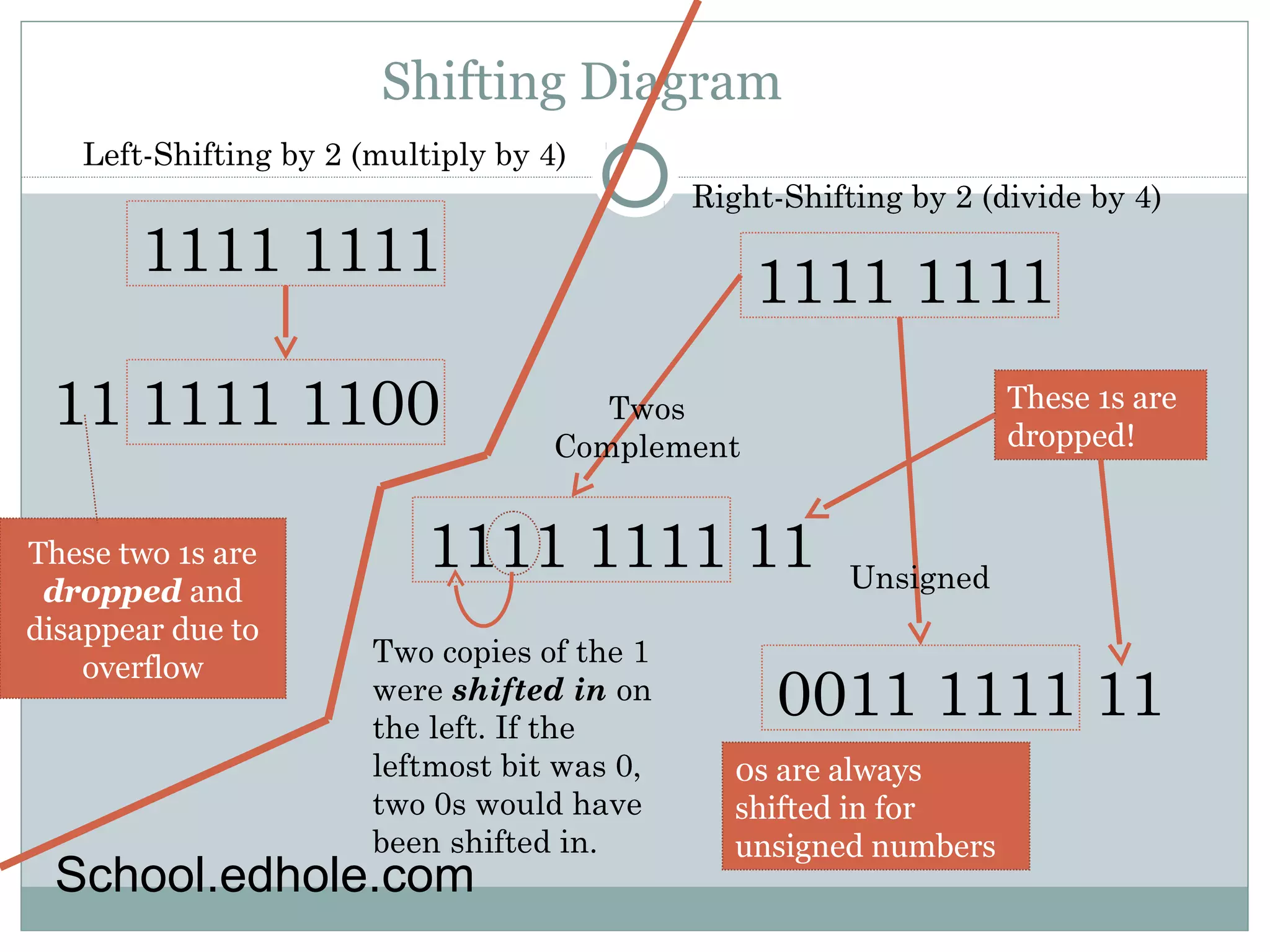
This document provides an overview of binary arithmetic concepts that are important for understanding how computers perform basic math operations. It discusses how binary addition and subtraction work, including the concepts of carrying digits and overflow. It also covers representing negative numbers using two's complement notation and how this allows subtraction to be performed by addition. Finally, it explains how multiplication and division can be accomplished in binary by shifting bits left or right, known as multiplication and division by powers of 2. The goal is to explain these fundamental binary math operations rather than focusing on calculating decimal values.

1. Top School in Delhi NCR
BY:
SCHOOL.EDHOLE.COM

2. Binary Arithmetic
MATH FOR COMPUTERS
School.edhole.com

3. Huh?
• Binary numbers are NUMBERS
• That means you can add, subtract, multiply, and
divide
• 2 + 2 = 4
• In Binary: 10 + 10 = 100
• So you COULD just convert all numbers to decimal,
do the math, and then convert the answer back…
• But I don’t care about the math
• I want you to understand how a computer does it!
School.edhole.com

4. Addition
Similar to addition of large decimal numbers
You need to “carry” when a number gets too large for
a single digit
In binary, that’s 1 + 1 = 10
carried bits
(or 0, carry a 1)
If you have 1 + 1 + 1 = 11
11_
(or 1, carry a 1)
11 0011
+ 1011
11 1110
School.edhole.com

5. Addition Practice
1110 + 1010
1001 + 111
1111 0000 + 1111
111 1000 + 1111
1000 1100 + 1100 0110
Take a few minutes to try them
 (answers in the PowerPoint Notes)
School.edhole.com

6. Overflow
1111 1111 + 100 = 1 0000 0011
The answer is more than 1 byte large
A computer typically will make it DROP THE
EXTRA BIT ON THE LEFT
The computer’s answer: 11 (binary) or 3
(decimal)
This is called an overflow error
Sometimes overflow behavior is undefined
(unpredictable)
School.edhole.com

7. Why overflow happens
A computer’s processor stores information in
something called a register.
Registers have a limited space – they can only
store a certain number of bits.
If a processor does a calculation and the answer
exceeds the capacity of the register, then the extra
bits are dropped
Modern registers are usually 16 or 32 bits, but for
this class we’ll only use 8 bits.
School.edhole.com

8. Addition Practice Pt. 2
Do the math, but give the answer an 8-bit computer
would give
1111 1111 + 1010
1010 1100 + 111 1111
1000 0000 + 1000 0000
1101 1010 + 1110 0110
 (answers in the PowerPoint Notes)
School.edhole.com

9. Negative Numbers for Computers
A computer needs a way to represent negative
numbers (there’s no “negative sign” in the comp)
One Idea:
Use one of the bits to indicate the sign of the
number, instead of using it as a digit
School.edhole.com

10. Sign Bit (the bad way)
So the 1st bit of a number indicates it’s sign
Examples:
00000010 is 2
10000010 is -2
School.edhole.com

11. Problem with sign bit system
2 zeros is a waste (10000000 and 00000000 are
both zero)
Computer processors can’t subtract without special
instructions
We need a way to subtract by adding!
Huh?
School.edhole.com

12. Twos Complement
• Consider this idea: a binary digit “place value”
could be negative!
negative
eights
fours twos ones
1 0 1 1
• So the above number is actually 3 (the positive
bits) minus 8 = -5
• 1000 in the above system actually represents the
decimal number -8
• The example above is 4 bits. Most problems for this
class will assume 8 bits.
School.edhole.com

13. Twos Complement cont.
REALLY IMPORTANT: Notice that with both
negative number systems you need to know
the number of total bits you are going to use!
We’ll assume 8 bits for simplicity.
What is the value of the “negative place”?
What is the new range of numbers? (Hint: It’s
not 0 – 255 anymore)
School.edhole.com

14. Calculating Twos Complement
• Example: -1 in (8-bit) twos complement is
1111 1111
• Still confused?
• Remember, everything is the same except for
a negative place value!
-128 64 32 16 8 4 2 1
1 1 1 1 1 1 1 1
• -128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = -1
• Btw, a “normal” binary number (where 1111
1111 = 255) is called “unsigned”
School.edhole.com

15. Calculating Twos Complement Pt. 2
• Shortcut: Convert the positive binary
number, switch all the bits (0s become 1s, 1s
become 0s), then add 1
• It only doesn’t work for -128 (no positive
number)
• Try some!
Set 1
• -127
• -23
• -8
• -100
Set 2
• -5
• -117
• -52
• -12
School.edhole.com

16. Actually Subtracting, finally
• Once you’ve got Twos Complement figured out,
subtracting is IDENTICAL TO ADDING (but now
using our twos complement numbers)
• Example: Decimal 100 - 20
• Binary: 0110 0100 - 0001 0100
• 2s complement of 20: 1110 1100
0110 0100
+1110 1100
1 0101 0000
• Overflow bit is dropped, as usual
• 0101 0000 is… 80
• So this 2s complement system USES overflow
School.edhole.com

17. Practice Excercises
Do in Binary (know how to do decimal conversions,
2s complement conversions, and binary addition)
Set 1
12 – 2
66 – 30
35 – 44
Set 2
• 50 - 10
• 2 - 1
• 127 - 128
School.edhole.com

18. Just to be clear:
If you have a binary number
like 1101 0110
It could be 214, or -42
There’s no way to tell if it’s negative just by looking
at it!
Assume it is positive, unless the problem states
otherwise.
School.edhole.com

19. Multiplication & Division
• We’ll just talk about multiplying and dividing by the
powers of 2
• This is called “shifting”
• Just like when you multiply or divide by 10, you just shift
the decimal point
• In binary, when you multiply or divide by 2, you shift the
“binary point”
• 4 * 2 = 8
• 100 * 10 = 1000
• 4 / 2 = 2
• 100 / 10 = 10
School.edhole.com

20. Shifting Details
• Multiplying can also be called left-shifting
• Dividing: right-shifting
• Left-Shifting can give you the overflow error
• 1000 0000 * 10 = 1 0000 0000
• For 2s complement negative numbers,
overflow will give really weird results
• Again, the leftmost bit is dropped
• Right-shift is DIFFERENT FOR TWOS
COMPLEMENT vs. unsigned binary numbers
• Unsigned: shift in a 0 for the leftmost bit
• 2s comp: shift School.edhole.co imn a COPY of the leftmost bit

21. Shifting Diagram
Left-Shifting by 2 (multiply by 4)
1111 1111
11 1111 1100
These two 1s are
dropped and
disappear due to
overflow
Right-Shifting by 2 (divide by 4)
1111 1111
1111 1111 11
0011 1111 11
Twos
Complement
Unsigned
Two copies of the 1
were shifted in on
the left. If the
leftmost bit was 0,
two 0s would have
been shifted in.
0s are always
shifted in for
unsigned numbers
These 1s are
dropped!
School.edhole.com

22. More Shifting Examples
Unsigned numbers
1011 0111 * 10 = 0110 1110 (overflow)
1111 1111 * 100 = 1111 1100 (overflow)
0001 1111 * 1000 = 1111 1000
1000 0000 / 1 0000 = 0000 1000
0011 0010 / 10 = 0001 1001
0001 0011 / 100 = 0000 0100 (?????)
19 / 4 = 4
So when you divide, you lose precision
(the computer will drop bits that go off
the right side – this means the answer
is always rounded down towards -∞)
Twos Complement
1111 1111 * 10 = 1111 1110
1000 0001 * 10 = 0000 0010 (overflow!)
-127 * 2 = 2…?
1001 1100 / 100 = 1110 0111
Instead of 0s, 1s
were shifted in on
the left because
that was the
leftmost bit of the
original byte
School.edhole.com

23. Fancy Shifting Animation: Multiplication
Also called left-shifting
(look at the animation)
This red box
is a register
0 1 1 0 1 0 1 1
0 0
Lets And Now So put the the the some bits bits processor that bits shift went into to gets the out an left register of instruction
the by register
3 (places
8 bits)
And are to der (the because multiply tohpapt new ewde empty b 8 wecoanu’ts this is the number spaces eg eotf 3rd ohvee power by are croflrorwect 8
filled of 2)
with zeros
Notic t answer,
because of overflow. If the original number was
smaller and had three zeros on the left, then the
overflow would have only dropped zeros, and
the answer would be accurate.
View this
slide in a
slide
show!
School.edhole.com

24. Negative Number Multiplication
Overflow
For Negative numbers, be aware that overflow
will yield some strange results
1 0 1 0 1 1 0 1
0
The computer erases the bit that overflowed and
puts in a zero on the right, like it’s supposed to. But
the new number is 01011010, which equals 90! This
happened because the lower limit of 8-bit twos
complement negative numbers is -128. However,
-83 * 2 would have gone below that.
Let’s multiply by 2. This means we left-shift by 1.
Take this 8-bit negative binary number:
10101101 = -83 (or positive 173)
View this
slide in a
slide
show!
School.edhole.com

25. Fancy Shifting Animation: Division
Also called right-shifting
(look at the
animation)
0 1 1
0
1 0 1 0 1 0 1 1
The computer Dividing drops by powers the bits of that 2 is went very similar
out of the
register to to multiplying. the right. If the Here, original we have number our
was
positive original (171), then binary the number computer in will the put register.
zeros on the
left. The (10101011 final answer = 171 is: OR 42. -Notice 85)
that this isn’t a
totally accurate answer (it should be 42.75) Because
the computer dropped some bits we lost precision.
Basically, the computer will always round down.
View this
slide in a
slide
show!
If the original Let’s try number dividing was by negative 4. When (-that 85), happens,
then the only
difference the number would be in that the ones register come will in shift on the to the
left side
instead right of zeros. by 2 This places. time (4 our is the answer 2nd power is -22. of It 2)
should be
-21.75, but the computer rounded down again. Just
remember that when you round a negative number
DOWN, it becomes more negative!
School.edhole.com

26. Microsoft Calculator
It’s actually useful for this binary stuff
Use it to double-check and test yourself
Put it into Scientific mode (under view) and you’ll see
buttons for decimal, binary, hex, and octal
School.edhole.com

27. Calculator Cont.
• If you click on the decimal (Dec) button and
then enter a negative decimal number, then
click the Binary (Bin) button, you’ll see that
negative number in Twos Complement form
• If you do any arithmetic in Binary, and the
Byte button is activated, you’ll see the
“computer’s answer” (overflow)
• You can then click over to Decimal to see what
that number would be
School.edhole.com

28. Shifting Excercises
• Convert to Binary, then give the computer’s
answers
• Use Calc for the initial conversions and answer-checking
• Btw, I use an asterisk (*) for multiplication
-50 * 2
10 / 2
12 * 4
-120 / 8
78 * 4
12 / 8
-100 * 2
-12 / 4
School.edhole.com

29. Restating the Obvious
The MATH ISN’T IMPORTANT. I can get the
answers from a calculator.
Understanding these processes gives you an idea of
how the computer works.
If the only thing you understand is that computers
are actually pretty simple machines that need lots
of instructions to work properly, then you’re doing
pretty good (ok, you won’t so well on the test if you
can’t do the calculations, but at least you have the
general idea)
School.edhole.com