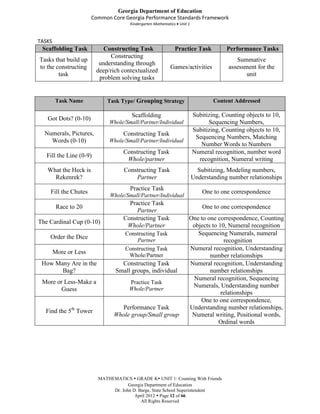
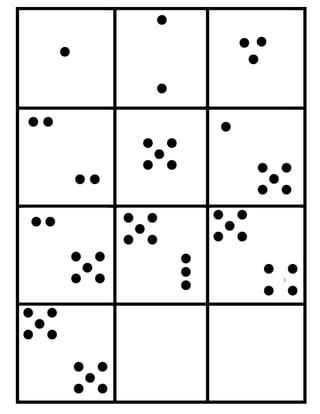
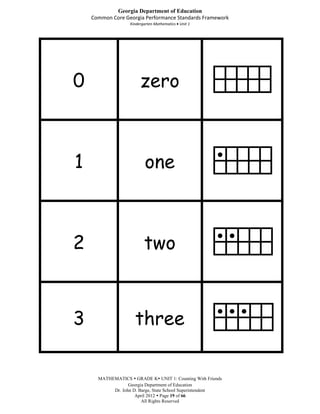
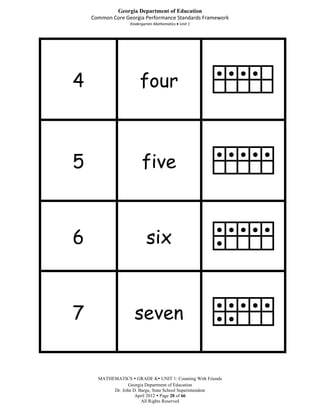
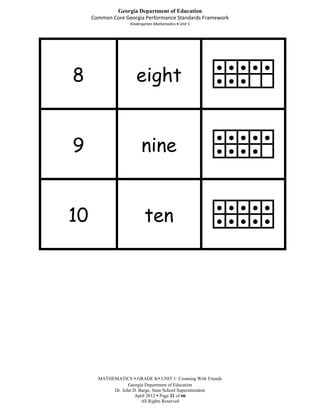
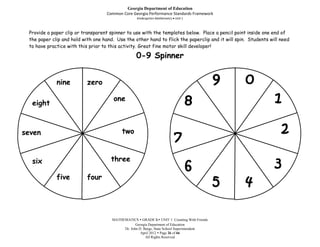
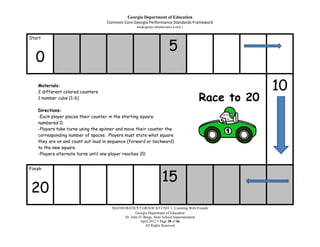
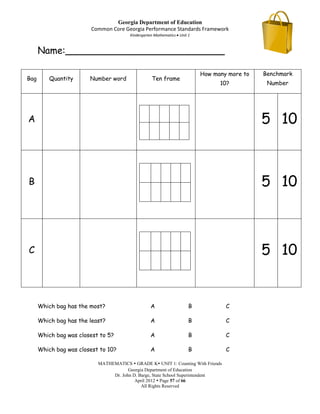
This document provides an overview, standards, and unit plan for a kindergarten mathematics unit on counting. The unit focuses on developing students' understanding of counting, including connecting counting to cardinality, counting objects accurately, and using numbers to represent quantities. The unit comprises 5 weeks and includes daily lessons, activities, and games to help students practice counting skills and build number sense.