The document is a mathematics textbook designed for Grade 6 students in the Philippines, published by Diwa Learning Systems Inc. It includes various mathematical topics such as whole numbers, fractions, decimals, geometry, and basic algebra, with a pedagogical focus on developing computational skills and an appreciation for mathematics through interactive and real-life problem-solving activities. The book emphasizes critical thinking, exercises, and assessments structured to enhance learning and understanding of mathematical concepts.

1. Math for Smart Kids 6

2. Math for Smart Kids
Grade 6
Textbook
Philippine Copyright 2010 by DIWA LEARNING SYSTEMS INC
All rights reserved. Printed in the Philippines
Editorial, design, and layout by University Press of First Asia
No part of this publication may be reproduced or transmitted in any form or by any means electronic or
mechanical, including photocopying, recording, or any information storage and retrieval systems, without
permission in writing from the copyright owner.
Exclusively distributed by
DIWA LEARNING SYSTEMS INC
4/F SEDCCO 1 Bldg.
120 Thailand corner Legazpi Streets
Legaspi Village, 1229 Makati City, Philippines
Tel. No.: (632) 893-8501 * Fax: (632) 817-8700
ISBN 978-971-46-0125-3
The Editorial Board
Authors
Dr. Estrella P. Mercado finished her PhD in Educational Management (with honor) and MA in Education at Manuel L. Quezon
University. She also holds an MEd in Special Education degree and a BS in Elementary Education degree from the Philippine
Normal University (PNU). She has been a classroom teacher, an Education supervisor, and an assistant chief of the Elementary
Division of the Department of Education, Culture and Sports (DECS-NCR). She was awarded as Outstanding Female Educator in
1998 by the Filipino Chinese Women Federation. She presently heads the Special Education Department at PNU.
Angelo D. Uy is currently pursuing his master’s degree in Mathematics Education at PNU, where he also obtained his BS in
Mathematics for Teachers. He was also a trainer in different Math competitions and a participant in various seminar-workshops
sponsored by the Mathematics Teachers Association of the Philippines. He taught at Hotchkiss Learning Center in Surigao del Sur
and at the De La Salle Santiago Zobel School in Ayala Alabang. He is presently a member of the faculty of Jacobo Z. Gonzales
Memorial National High School in Biñan, Laguna.
Consultant
Ma. Portia Y. Dimabuyu holds an MA in Education degree, major in Mathematics, and a BS Education degree, major in
Mathematics, from the University of the Philippines-Diliman. She was a recipient of the Excellence in Mathematics Teaching
Award in 2007 from the UP College of Education. She is presently an Assistant Professor at the Mathematics Department of UP
Integrated School and a lecturer of undergraduate and graduate courses in teaching Mathematics at the UP College of Education.
Reviewer
Reina M. Rama has a bachelor’s degree in Mathematics from Silliman University and is currently pursuing her master’s
degree in Mathematics from Ateneo de Manila University. Before teaching full time, she was a researcher/teacher-trainer at the
University of the Philippines-National Institute of Science and Mathematics Education Development (UP-NISMED). She taught
Mathematics at Colegio de San Lorenzo and Miriam College. She is the Subject Coordinator for Mathematics Area of Miriam
College-High School Unit.

3. Preface
Math for Smart Kids is a series of textbooks in Mathematics for grade school,
which is designed to help pupils develop appreciation and love for mathematics.
This series also aims to help the learners acquire the skills they need to become
computationally literate.
The lessons in each textbook present mathematics concepts and principles that
are anchored on the competencies prescribed by the Department of Education. Each
lesson starts with Let’s Do Math, where mathematics concepts and principles are
introduced through problems, stories, games, or puzzles. This section is followed by
Let’s Look Back, which lists questions that will help the pupils to think critically on
what has been introduced in the lesson and allow them to discover things on their
own. For easy recall of important points or concepts taken up in a lesson, the section
Let’s Remember Our Learning has been included. Multilevel exercises are provided in
Let’s Practice and Let’s Test Our Learning that will assess how much the pupils have
learned from the lesson. The exercises will also determine if the pupils are ready to
learn new mathematics skills. The development of the multiple intelligences of an
individual is reflected in the different activities that the pupils will perform—from
concrete to semi-concrete, and from semi-abstract to abstract kind of learning.
Situations and real-life problems are provided in Let’s Look Forward to give the pupils
opportunities to apply what they have learned to their daily life experiences.
This series of textbooks gives the learners the opportunity to explore and enjoy
Mathematics. Let’s have fun learning together!
The Authors

4. Table of Contents
Unit 1 Whole Numbers, Number Theory, and Fractions
Chapter 1 Review of Whole Numbers
Lesson 1 Properties of Operations………………………………………… ......................2
2 Exponents ...........................................................................................6
3 Order of Operations ............................................................................9
4 Problem Solving Involving Series of Operations ................................. 12
Chapter 2 Number Theory
Lesson 1 Divisibility ........................................................................................ 19
2 Prime Factorization............................................................................ 25
3 Greatest Common Factor ................................................................... 31
4 Least Common Multiple .................................................................... 36
Chapter 3 Fractions
Lesson 1 Equivalent Fractions .......................................................................... 41
2 Reducing Fractions to Lowest Terms ................................................. 47
3 Changing Mixed Numbers to Improper Fractions, and Vice Versa ...... 51
1
4 Fractions Close to 0, , and 1 ........................................................... 55
2
5 Comparing Fractions ......................................................................... 59
6 Ordering Fractions ............................................................................ 65
Chapter 4 Operations on Fractions
Lesson 1 Addition and Subtraction of Similar Fractions
and Mixed Numbers .......................................................................... 69
2 Addition and Subtraction of Dissimilar Fractions
and Mixed Numbers .......................................................................... 75
3 Mental Addition and Subtraction of Fractions .................................... 82
4 Multiplication of Fractions ................................................................ 86
5 Division of Fractions ......................................................................... 93

5. Unit 2 Decimals, Ratio, Proportion, and Percent
Chapter 5 Decimals
Lesson 1 Place Values of Decimals ................................................................. 102
2 Changing Fractions to Decimals, and Vice Versa .............................. 107
3 Comparing and Ordering Decimals .................................................. 111
4 Rounding off Decimals ................................................................... 117
Chapter 6 Operations on Decimals
Lesson 1 Addition and Subtraction of Decimals .............................................. 121
2 Mental Addition of Decimals ........................................................... 127
3 Problem Solving Involving Addition and Subtraction
of Decimals ..................................................................................... 131
4 Multiplication of Decimals............................................................... 136
5 Estimation of Decimal Products ....................................................... 141
6 Mental Multiplication of Decimals ................................................... 145
7 Division of Decimals ....................................................................... 148
8 Estimation of Decimal Quotients ..................................................... 154
9 Mental Division of Decimals............................................................ 157
10 Problem Solving Involving Two or More Operations
on Decimals .................................................................................... 162
Chapter 7 Ratio and Proportion
Lesson 1 Ratio and Proportion ....................................................................... 167
2 Direct, Inverse, and Partitive Proportions ........................................ 173
Chapter 8 Percent
Lesson 1 Percents, Fractions, and Decimals .................................................... 181
2 Finding the Percentage, Rate, and Base ............................................ 186
3 Applications of Percent .................................................................... 194
Unit 3 Geometry and Measurement
Chapter 9 Geometry
Lesson 1 Subsets of a Line ............................................................................. 206
2 Angles ............................................................................................. 210
3 Polygons and Circles ....................................................................... 215
4 Space Figures .................................................................................. 224

6. Chapter 10 Measurement
Lesson 1 Surface Area of Basic Solids ............................................................. 228
2 Volume of Solids ............................................................................. 237
3 Meter Reading ................................................................................ 245
4 Metric Conversion ........................................................................... 252
Unit 4 Statistics, Probability, and Introduction to Algebra
Chapter 11 Statistics and Probability
Lesson 1 Circle Graph ................................................................................... 256
2 Mean, Median, and Mode ................................................................ 266
3 Possible Outcomes .......................................................................... 270
4 Simple Probability ........................................................................... 274
Chapter 12 Introduction to Algebra
Lesson 1 Integers ........................................................................................... 278
2 Comparing Integers ......................................................................... 282
3 Ordering Integers ............................................................................ 286
4 Algebraic Expressions and Equations ............................................... 290
Glossary …………………………………………………………………………... ...................... 293
Bibliography ........................................................................................................ 296
Index ................................................................................................................... 297

7. Unit
1
Whole Numbers, Number
Theory, and Fractions

8. Chapter 1
Review of Whole Numbers
Lesson 1 Properties of Operations
Mr. Cruz planted 20 tomatoes and 35 ampalaya plants in one of his garden plots.
Then, he planted 35 tomatoes and 20 ampalaya plants in another plot. Compare the
combined number of tomatoes and ampalaya plants in the two plots. What do you
observe?
plot A plot B
20 + 35 = 35 + 20
55 = 55
Mr. Cruz has the same number of plants in both garden plots, that is, 55.
The above equation illustrates the commutative property of addition. This
property states that the order of the addends does not change the sum.
Look at this other example.
Mr. Cruz planted 5 rows of eggplants with 6 eggplants in each row of his garden.
In another garden, he had 6 rows of okra plants with 5 okra plants in each row.
Math for Smart Kids 6

9. Compare the number of eggplants with the number of okra plants. What do you
observe?
eggplants okra plants
56 = 65
30 = 30
The number of eggplants and the number of okra plants are the same, that is, 30.
In the above equation, the symbol used for multiplication is the multiplication
dot (⋅). The equation shows the commutative property of multiplication. This
property states that the order of the factors does not affect the product.
Aside from the commutative property, there are other properties of operations
that you should know about.
Other Properties of Operations
Operation
Property
Addition Multiplication
5 + (6 + 9) = (5 + 6) + 9 6  (2  3) = (6  2)  3
Associative property 5 + (15) = (11) + 9 6  (6) = (12)  3
20 = 20 36 = 36
7+0=7 71=7
Identity property
8+0=8 81=8
Zero property of 70=0
multiplication 25  0 = 0
Distributive property 9  (2 + 3) = (9  2) + (9  3)
of multiplication over 9  (5) = (18) + (27)
addition 45 = 45
Inverse property of  1
5  =1
multiplication  5
1. What are the properties of operations?
2. What is the identity element for addition? for multiplication?
Whole Numbers, Number Theory, and Fractions

10. These are the properties of operations:
1. Commutative property – The order of the addends or factors does not change
the sum or the product.
2. Associative property – The grouping of the addends or factors does not
change the sum or the product.
3. Identity property of addition – Any number added to 0 will give the number
itself. Zero (0) is the identity element for addition.
4. Identity property of multiplication – Any number multiplied by 1 will give the
number itself. One (1) is the identity element for multiplication.
5. Zero property of multiplication – Any number multiplied by 0 will give a
product of 0.
6. Distributive property of multiplication over addition – The product of a number
and the sum of two or more addends is equal to the sum of the products of
that number multiplied to each of the addends.
7. Inverse property of multiplication – Any number multiplied by its reciprocal will
give a product of 1.
A. Supply the missing number and identify the property used. The first one has
been done for you.
1. 25 + 35 = 35 + 25 Commutative property of addition
2. 85  25 = 25  __________________________________
3. 85  =0 __________________________________
4.  75 = 75 __________________________________
5. 100 + = 100 __________________________________
6. 12 + (13 + 26) = (12 + 13) + __________________________________
7. (89  2)  14 = 89  (2  ) __________________________________
8. 32  (5 + 8) = (32  ) + (32  ) __________________________________
9. 45   1  =
 45  __________________________________
 
10. 89 + (24 + 25) = ( + 24) + 25 __________________________________
Math for Smart Kids 6

11. B. Identify the property of operation shown in each equation.
_________________________ 1. 7  (32 + 4) = (7  32) + (7  4)
_________________________ 2. 89 + (45 + 32) = (89 + 45) + 32
_________________________ 3. 360 + 0 = 360
_________________________ 4. 39  3 = 3  39
_________________________ 5. 85  (3  40) = (85  3)  40
_________________________ 6. 1  720 = 720
_________________________ 7. 45 + 89 = 89 + 45
_________________________ 8. 39  (40 + 32) = (39  40) + (39  32)
_________________________ 9. (36 + 34) + 45 = 36 + (34 + 45)
1
_________________________10. 37    = 1
 37 
 
Read and solve the following problems carefully.
1. Mother gave Rosa P45 while Father gave her P39. Mother gave Sonny P39
while Father gave him P45. Who had more money, Rosa or Sonny? Explain
your answer.
2. Eloisa gathered 20 chicos on Sunday, 32 chicos on Monday, and 45 chicos on
Tuesday. Renato gathered 32 chicos on Sunday, 45 chicos on Monday, and
20 chicos on Tuesday. Who had more chicos, Eloisa or Renato? Explain your
answer.
Explain why both sides of the equations are equal.
1. 41 + (24 + 69) = (41 + 24) + 69
2. 89  (3 + 8) = (89  3) + (89  8)
3. 179 + 184 = 184 + 179
4. 85  79 = 79  85
5. (46 + 39)  62 = (46  62) + (39  62)
Whole Numbers, Number Theory, and Fractions

12. Lesson 2 Exponents
Scientists and engineers who often use very large or very small numbers find it
useful to write these numbers this way:
1. 9.46 × 1015 meters (m) – the distance light travels in one year
2. 1.9891 × 1030 kilograms (kg) – the mass of the sun
Observe how the two numbers are written. The numbers 1015 and 1030 are
written in exponential form. The number 10 is called base. The base is the number
multiplied by itself. The numbers written at the upper right-hand side of the base (15
and 30) are called exponents. The exponent indicates how many times the base is to
be multiplied by itself. The value of an exponential expression after multiplying the
base by itself as many times as indicated by the exponent is called power.
Here are some examples of numbers written in exponential form and expanded
form.
Exponential
Base Exponent Expanded Form Power
Form
30 3 0 1
52 5 2 55 25
43 4 3 444 64
65 6 5 66666 7 776
79 7 9 777777777 40 353 607
1002 100 2 100  100 10 000
1. What do you call the number written at the upper right-hand side of the base?
2. What does this number tell you?
3. How do you find the value of a number written in exponential form?
Math for Smart Kids 6

13. In ax = y , a is the base, x is the exponent, and y is the power or value of the
expression.
The power or value (y) of a number with exponent is computed by multiplying
the base (a) by itself as many times as indicated by the exponent (x).
The value of any nonzero number raised to the zero power is equal to 1.
A. Complete the table. Identify the base, exponent, and power of each number
written in exponential form.
Exponential
Base Exponent Power
Form
1. 107
2. 394
3. 873
4. 2502
5. 3403
B. Write the following in expanded form.
1. 532 _______________________________
2. 105 _______________________________
3. 273 _______________________________
4. 854 _______________________________
5. 767 _______________________________
6. 956 _______________________________
7. 398 _______________________________
8. 4010 _______________________________
9. 459 _______________________________
10. 2604 _______________________________
Whole Numbers, Number Theory, and Fractions

14. A certain bacterium reproduces exponentially. If 10n is the number of bacteria in
n days, how many of these bacteria will be present after 15 days? Write the answer in
expanded and exponential forms.
Perform the indicated operations on the following exponential expressions. An
example has been provided for you.
Example: 23 + 32 = (2  2  2) + (3  3)
=8+9
= 17
1. 35 + 43 ___________________________________________________________________________________________________________
2. 29 − 27 ___________________________________________________________________________________________________________
3. 19  56 ___________________________________________________________________________________________________________
4. 105  54 ___________________________________________________________________________________________________________
5. 163 − 54 ___________________________________________________________________________________________________________
6. 117  116 ___________________________________________________________________________________________________________
7. 20 + 50 + 4341 ___________________________________________________________________________________________________________
8. 73 + 84 + 25 ___________________________________________________________________________________________________________
9. (93 − 28) + 75 ___________________________________________________________________________________________________________
10. (95  73)  92 ___________________________________________________________________________________________________________
Math for Smart Kids 6

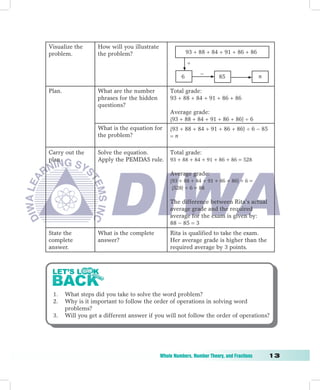
15. Lesson 3 Order of Operations
Letty’s transportation fare to school is P15. She spends the same amount for her
fare in going home. Letty also spends P30 for snacks and P50 for lunch. If her daily
allowance is P150, how much money would she have left at the end of the day?
To find the answer, you have to perform a series of operations.
1. How much does Letty spend for her fare, snacks, and lunch in a day?
n = (15  2) + 30 + 50
2. How much money would she have left at the end of the day if her daily
allowance is P150?
n = 150 − [(15  2) + 30 + 50]
= 150 − [(30) + 30 + 50]
= 150 − [110]
= 40
Therefore, Letty has P40 left at the end of the day.
To solve an equation that involves a series of operations, you must follow the
PEMDAS rule:
P − Do the operation inside the parentheses first.
E − Evaluate the expressions with exponents.
M
− Multiply or divide from left to right, whichever comes first.
D
A
− Add or subtract from left to right.
S
Whole Numbers, Number Theory, and Fractions

16. Study these other examples.
1. n = 35² + (32  5) ÷ 5 Do the operation inside the parentheses. Evaluate
= 1 225 + 160 ÷ 5 the expression with exponents.
= 1 225 + 32 Divide, then add.
= 1 257
2. n = (2  5) − (6  4 ÷ 8) Do the operation(s) inside the parentheses.
= (10) − (3) Multiply, then divide.
= 10 − 3 Subtract.
=7
3. n = (6 − 4 + 2)² + 8  6 Do the operation(s) inside the parentheses.
= (2 + 2)² + 8  6 Evaluate the expression with exponents.
= 16 + 8  6 Multiply, then add.
= 16 + 48
= 64
4. n = (5 + 2)  10² − 10 Do the operation inside the parentheses.
= 7  10² − 10 Evaluate the expression with exponents.
= 7  100 − 10 Multiply, then subtract.
= 700 − 10
= 690
1. What rule must you follow to perform a series of operations?
2. Which operation must you do first? Why?
3. Which operation must you do last? Why?
To solve an equation that involves a series of operations, follow the PEMDAS rule.
P – Do the operation inside the parentheses first.
E – Evaluate the expressions with exponents.
M
– Multiply and divide from left to right, whichever comes first.
D
A
– Add and subtract from left to right.
S
10 Math for Smart Kids 6

17. A. Write the order of operations to be performed.
1. 103 + (8  4) 2  4 = n ______________________________________________
2. 44  20 − (85 ⋅ 2) = n ______________________________________________
3. (92  45)  10 − 400 = n ______________________________________________
4. 122 + (86  5)  10 = n ______________________________________________
5. 104 − (45  87) + 999 = n ______________________________________________
6. (145  3) + (97  2) – 229 = n ______________________________________________
7. (985 + 5)  10 − 98 = n ______________________________________________
8. 396 + 492  7 − 586 = n ______________________________________________
9. 625  5 + 701 − 289 = n ______________________________________________
10. 798 + 42  3 − 375 = n ______________________________________________
B. Find the value of n in Exercise A. Show every step of your solution on a separate
sheet of paper.
Andrea plans to spend her summer vacation in Boracay. She needs P5 000 for the
one-way airfare, P3 000 for the one-day hotel accommodation, and P2 000 for one-day
meals. How much does Andrea need, including the two-way air fare, if she will spend
her summer vacation in Boracay for 7 days?
Find the value of n. Show every step of your solution. Do this on a separate sheet
of paper.
1. 375 + 3  878 − 245 = n 6. (140 − 101) + 10  2 = n
2. 104 + (92  4) − 304 = n 7. (784  4)  2 + 1 589 − 379 = n
3. (87  9) + 63  8 = n 8. (475  5)  (45 – 85) = n
4. 105 + (810  9) − 45 = n 9. 37 804 − 439  8 + 6 000 = n
5. (38  5) + 10 + 169 = n 10. 105 − 82  81 + 37 809 = n
Whole Numbers, Number Theory, and Fractions 11

18. Lesson 4 Problem Solving Involving a Series
of Operations
Rita got the following grades in her subjects.
93, 88, 84, 91, 86, and 86
If the required average for the entrance examination to a science high school is 85
or higher, would she be qualified to take the exam? By how much less or more is her
average grade compared with the required average?
To solve the problem, follow these steps:
Understand What facts are given in • Rita’s grades: 93, 88, 84, 91, 86,
and analyze the the problem? 86
problem. • Average required is 85 or higher.
What is asked in the • Is Rita qualified or not to take the
problem? entrance exam?
• By how much less or more is her
average grade compared with the
required average?
What are the hidden • What is Rita’s total grade in all
questions? her subjects?
• What is Rita’s average grade?
What operations will Addition, division, subtraction
you use?
1 Math for Smart Kids 6

19. Visualize the How will you illustrate
problem. the problem? 93 + 88 + 84 + 91 + 86 + 86

6 − 85 n
Plan. What are the number Total grade:
phrases for the hidden 93 + 88 + 84 + 91 + 86 + 86
questions?
Average grade:
(93 + 88 + 84 + 91 + 86 + 86)  6
What is the equation for (93 + 88 + 84 + 91 + 86 + 86)  6 − 85
the problem? =n
Carry out the Solve the equation. Total grade:
plan. Apply the PEMDAS rule. 93 + 88 + 84 + 91 + 86 + 86 = 528
Average grade:
(93 + 88 + 84 + 91 + 86 + 86)  6 =
(528)  6 = 88
The difference between Rita’s actual
average grade and the required
average for the exam is given by:
88 − 85 = 3
State the What is the complete Rita is qualified to take the exam.
complete answer? Her average grade is higher than the
answer. required average by 3 points.
1. What steps did you take to solve the word problem?
2. Why is it important to follow the order of operations in solving word
problems?
3. Will you get a different answer if you will not follow the order of operations?
Whole Numbers, Number Theory, and Fractions 1

20. To solve word problems involving a series of operations, follow these steps:
1. Understand and analyze the problem. Find out what facts are given, what is
asked in the problem, what the hidden questions are, and what operations will
be used.
2. Visualize the problem. Draw a diagram to illustrate the problem.
3. Plan to solve the problem. Write the number phrases for the hidden questions
and the equation for the problem.
4. Carry out the plan. Solve the equation by applying the PEMDAS rule.
5. State the complete answer.
A. Read and solve each problem. Follow the steps in problem solving and the rule
on the order of operations.
Problem 1 Problem 2
A laundrywoman There are 8 classrooms
earns P350 in one day. in a building. If the desks
If she spends P15 on in each classroom are
transportation and P100 arranged in 4 columns
on meals daily, how much and 10 rows, how many
money will she have left desks are there in the
after 3 days? building?
Understand and analyze
the problem
• What facts are given in
the problem?
• What is asked in the
problem?
• What is/are the hidden
question(s)?
• What operation(s) will
you use?
1 Math for Smart Kids 6

21. Visualize the problem.
• How will you illustrate
the problem?
Plan.
• What is/are the
number phrase(s) for
the hidden question(s)?
• What is the equation
for the problem?
Carry out the plan.
• Solve the equation.
State the complete
answer.
• What is the complete
answer?
B. Read and solve each problem. Show your solutions on a separate sheet of paper.
1. A landowner owns 6 hectares (ha) of farmland. He harvested 340 sacks of
palay from each hectare of farmland. He set aside 90 sacks to be divided
among his helpers and stored the rest equally in his 5 kamaligs. How many
sacks of palay were stored in each kamalig?
2. A supermarket has a delivery of P370 450 worth of canned goods and
P232 370 worth of kitchenware. The manager gives P200 000 as initial
payment and will pay the remaining amounts in 5 installments. How much
will each installment be?
3. Nena gathered 7 350 eggs from the poultry house. Her husband gathered
3 850 eggs more. They delivered the eggs equally to 50 vendors. How many
eggs did each vendor get?
4. A school choir held a concert for three days to raise funds. The choir
members were able to raise P6 900 on the first day, P2 500 on the second
day, and P10 550 on the third day. If they spend P500 on transportation and
P900 for miscellaneous expenses for a day, how much money do they have
left after three days?
5. A golf club had 148 members last month. Eighty-six new members joined the
club this month. Thirty-five club members from last month will no longer
renew their membership. How many members would the golf club have this
month?
Whole Numbers, Number Theory, and Fractions 1

22. Study the pictures below. Write five word problems using the given information
and solve them on a separate sheet of paper.
School Supplies
P30
P600
P25 P12 P500
A. Read and analyze the problem. Answer the questions that follow by encircling
the letter of your answer.
Mr. Fernando harvested 8 500 coconuts last week and 9 800 coconuts
this week. He gave his helpers 300 coconuts. If a truck can load 600
coconuts in one trip, how many trips does the truck need to make to
transport the remaining harvested coconuts?
1. What facts are given in the problem?
a. 8 500 coconuts, 9 800 coconuts, 300 helpers, 600 trips
b. 8 500 coconuts, 9 800 coconuts, 300 coconuts, 600 coconuts per trip
c. 8 500 coconuts, 9 800 coconuts, 300 coconuts given away, 600 coconuts
per trip
1 Math for Smart Kids 6

23. 2. What is asked in the problem?
a. number of trips
b. number of coconuts per trip
c. number of coconuts per hectare
3. What are the hidden questions?
a. How many trips need to be made? How many coconuts are to be
transported?
b. How many coconuts are transported per trip? How many coconuts are
left?
c. How many coconuts were harvested in all? How many coconuts are to
be transported?
4. What operations will be used?
a. addition, subtraction, and division
b. addition, division, and multiplication
c. addition, subtraction, and multiplication
5. What is the equation for the problem?
a. (8 500 + 9 800 – 300)  600 = n
b. [(8 500 − 9 800) + 300]  600 = n
c. [(9 800 + 8 500)  300]  600 = n
6. What is the complete answer?
a. There will be 3 trips.
b. There will be 30 trips.
c. There will be 300 trips.
B. Solve these problems.
1. There were 36 male volleyball players and 40 female volleyball players
during an athletic meet. Fifty-two of them participated in the meet last year.
How many volleyball players were not part of last year’s athletic meet?
2. During the orientation for the new students, 289 students were present. Of
these, 109 were not first year students. If 2 of the first year students were
3
female, how many male first year students were there?
Whole Numbers, Number Theory, and Fractions 1

24. 3. Gina can decorate 25 baskets in the morning and 20 baskets in the afternoon.
If she continues to work at this rate, how many baskets can she decorate in
4 weeks?
4. Harry sold 460 tickets for their school’s benefit concert. For every 5 tickets
he sold, Harry earned P8. How much did he earn from selling the tickets?
5. Roy earned P575 from selling barbecue. Jim earned P195 more than Roy.
Dan earned twice as much as Jim. How much is the total earning of the three
boys?
6. Mr. Lacson takes public transportation in going to work. He rides a tricycle
and pays P14 for his fare. He also rides a jeepney and pays P12 for his fare.
How much is his daily fare if he also rides a jeepney and a tricycle in going
home?
7. Two members of an organization are selling tickets for a benefit concert.
Member A sold 62 tickets, while member B sold 76 tickets. How much did
the two members earn from selling the tickets if each ticket costs P15?
8. Mother gave me P35. Father gave me P40. How many notebooks can I buy if
a notebook costs P15 each?
9. Mariel sold 3 blouses and 2 pairs of pants for P2,100. If the blouses cost P350
each, how much did each pair of pants cost?
10. Carmen bought 12 notebooks at P25 each and 10 pencils at P7 each. She sells
the notebooks for P26.50 each and the pencils for P7.75 each. How much
profit would she make if she will be able to sell all the items?
1 Math for Smart Kids 6

25. Chapter
Number Theory
Lesson 1 Divisibility
Angelo has 24 oranges. He wants to divide the oranges equally among his
3 sisters. Is it possible to divide the oranges equally among his 3 sisters? If yes, how
many oranges will each one get?
To answer this problem, you need to divide 24 by 3.
8
3) 24
24
− 24
0
Based on the solution, there is no remainder after dividing 24 by 3. Therefore,
Angelo’s sisters will have the same number of oranges and each of them will get 8
oranges.
The idea of having no remainder after dividing two numbers is called divisibility.
A whole number is divisible by another whole number if, after dividing, the
remainder is zero. However, you can determine if a whole number is divisible by
another whole number even without performing division. This can be done by
applying the divisibility rules.
Whole Numbers, Number Theory, and Fractions 1