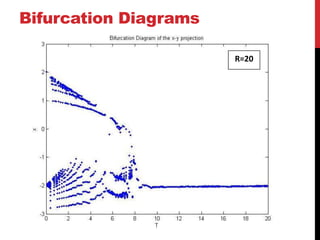
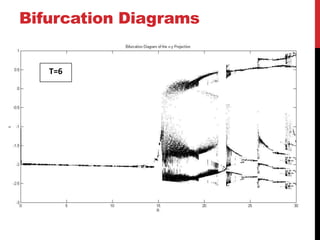
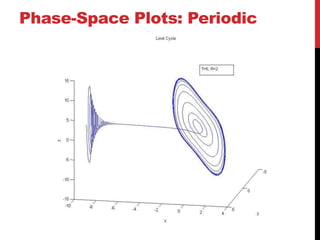
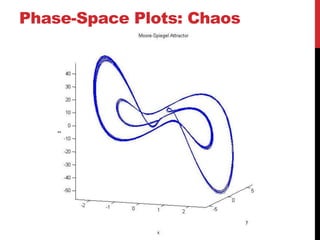
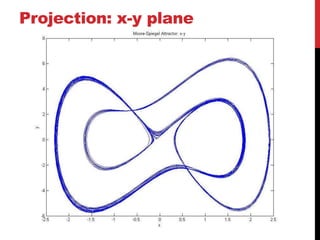
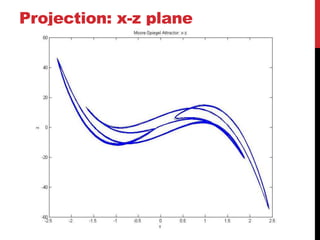
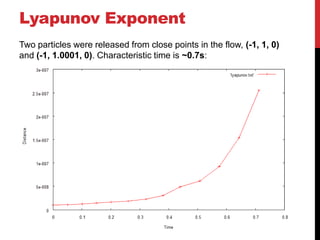
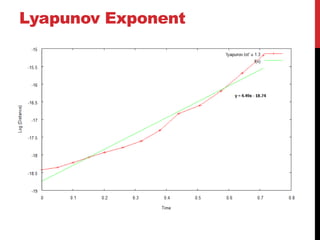
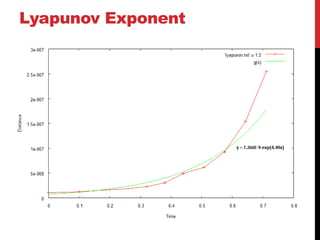
This document discusses the Moore-Spiegel oscillator, a nonlinear oscillator model used to study chaos. It provides the system equations, finds periodic and chaotic solutions using numerical integration, and analyzes the dynamics through phase space plots, Poincare sections, bifurcation diagrams, and Lyapunov exponents. The analysis reveals transitions from periodic to chaotic behavior as the control parameters are varied.

1. THE MOORE-SPIEGEL
OSCILLATOR
ABHRANIL DAS

2. The System

3. Fixed Points and Stability

4. Numerical Root-finding
% Newton-Raphson method to find roots
disp 'Newton-Raphson Method'
syms x;
i=0;
f=input('f: '); % User inputs function here
y=input('seed x: '); % and seed value here
while (abs(subs(f,x,y)/subs(diff(f),x,y))>1e-15) % termination criterion
y=y-subs(f,x,y)/subs(diff(f),x,y);
i=i+1;
end
x=y % print result
i % and iterations
% Bisection method to find roots
disp 'Bisection Method'
a=input('a: '); % start
b=input('b: '); % and end of starting interval
j=0; % iteration count
syms x;
while (b-a>0.000001) % termination criterion
mid=(a+b)/2;
if subs(f,x,b)*subs(f,x,mid)<0
a=mid;
else
b=mid;
end
j=j+1;
end
x=mid
j

5. Roots for T=6 and R=20
Root Seed (Newton- Interval
Raphson) (Bisection)
3 5 [0,5]
0.4495 0 [0,1]
-4.4495 -5 [-5,0]

6. Phase-Space Plots with RK4/5 (General Code)
t=10; N=10000; h=float(t)/N; l=range(3)
T=6; R=20
x=list(input('Starting x,y,z: '))
file=open('msplot.txt', 'w')
def f(x):
return [x[1], x[2], -x[2]-(T-R+R*x[0]**2)*x[1]-T*x[0]]
for iter in range(N):
print>> file, x[0],x[1],x[2]
k1=[h*f(x)[i] for i in l]
k2=[h*f([(x[j]+k1[j]/2) for j in l])[i] for i in l]
k3=[h*f([(x[j]+k2[j]/2) for j in l])[i] for i in l]
k4=[h*f([(x[j]+k3[j]) for j in l])[i] for i in l]
x=[x[i]+(k1[i]+2*k2[i]+2*k3[i]+k4[i]) for i in l]
file.close()
import Gnuplot
g=Gnuplot.Gnuplot()
g('''splot 'msplot.txt' w l''')
g('pause -1')
global T;
global R;
T=0;
R=20;
[tarray,Y] = ode45(@mseq,[0 1000],[-1 1 0]);
function dy = mseq(t,y)
global T;
global R;
dy = zeros(3,1);
dy(1) = y(2);
dy(2) = y(3);
dy(3) = -y(3)-(T-R+R*y(1)^2)*y(2)-T*y(1);
end

7. Phase-Space Plots: Periodic

8. Phase-Space Plots: Chaos

9. Projection: x-y plane

10. Projection: x-z plane

11. Projection: y-z plane

12. Lyapunov Exponent
Two particles were released from close points in the flow, (-1, 1, 0)
and (-1, 1.0001, 0). Characteristic time is ~0.7s:

13. Lyapunov Exponent

14. Lyapunov Exponent

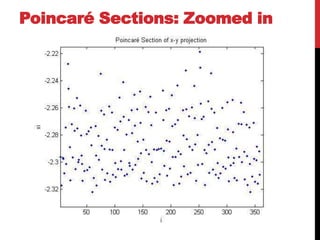
15. Poincaré Sections of projections
P=[];
for i=1:length(Y)-1
if (Y(i,2))<0 && (Y(i+1,2))>0
P(end+1)=Y(i,1);
end
end
P=P';
plot(P,'.');

16. Poincaré Sections: Zoomed in

17. Bifurcation Diagrams
global T;
global R;
T=0;
R=20;
B=[];
while T<20
[tarray,Y] = ode45(@mseq,[0 1000],[-1 1 0]);
P=[];
for i=1:length(Y)-1
if (Y(i,2))<0 && (Y(i+1,2))>0
P(end+1)=Y(i,1);
end
end
P=P';
P=P(end-10:end);
for i=1:length(P)
B(end+1,:)=[T P(i)];
end
T=T+.1
end

18. Bifurcation Diagrams
R=20

19. Bifurcation Diagrams
T=6

20. Reference
Algebraically Simple Chaotic Flows, J.C. Sprott, S J. Linz,
Intl. J. of Chaos Theory and Applications
A Thermally Excited Non-linear Oscillator, D.W. Moore, E.A.
Spiegel, Astrophysical Journal