This document contains 19 multiple choice questions from an exam on various math topics, including functions, inequalities, geometry, vectors, matrices, and limits. The questions cover finding minimum values of functions, determining intervals for variables, properties of functions, volumes of solids of revolution, solutions to inequalities, relationships between line and circle segments, determinants, limits, and symmetries of points across planes. The document also provides a key with the correct answer for each question labeled 1 through 19.

1. EFOOM 2020
1
01. (Efomm 2020) Sejam as funções reais f e g definidas por 4 3 2
f(x) x 10x 32x 38x 15
= − + − + e
3 2
g(x) x 8x 18x 16.
=
− + − + O menor valor de | f(x) g(x) |
− no intervalo [1; 3] é
a) 1
b) 2
c) 4
d) 5
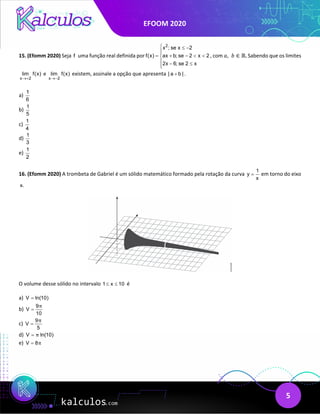
e) 7
02. (Efomm 2020) Seja a função 𝑓𝑓: [𝑡𝑡; +∞] → ℝ, definida por 3 2
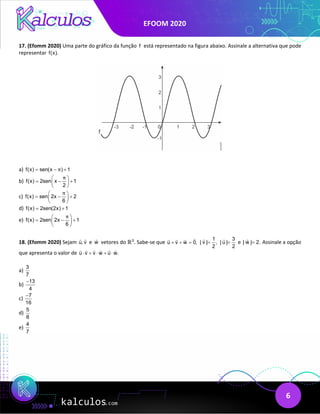
f(x) x 3x 1.
= − + O menor valor de t, para que a função
seja injetiva, é
a) 1
−
b) 0
c) 1
d) 2
e) 3
03. (Efomm 2020) Seja 𝑓𝑓: ℕ → ℕ uma função tal que f(m n) n f(m) m f(n)
⋅ = ⋅ + ⋅ para todos os naturais m e n. Se
f(20) 3, f(14) 1,25
= = e f(35) 4,
= o valor de f(8) é
a) 1
b) 2
c) 3
d) 4
e) 5
04. (Efomm 2020) Quantos são os anagramas da palavra MERCANTE que possuem a letra M na 1ª posição (no caso, a
posição de origem), ou a letra E na 2ª posição, ou a letra R na 3ª posição?
a) 60
b) 120
c) 10920
d) 12600
e) 15120

2. EFOOM 2020
2
05. (Efomm 2020) Assinale a alternativa que apresenta o termo independente de x na expansão binomial
8
2
6
1
x .
x
 
+
 
 
a) 1
b) 8
c) 28
d) 56
e) 70
06. (Efomm 2020) Considere um recipiente cúbico W de aresta 2. Suponha que possamos colocar 8 esferas de raio R
e uma de raio 2R dentro de W dispostas do seguinte modo: a esfera de raio 2R tem seu centro coincidindo com o centro
de W e cada uma das demais esferas são tangentes a três faces e à esfera maior. Assinale a opção que apresenta o
intervalo ao qual R pertença.
Dados: 2 1.4, 3 1.7
= = e 5 2.2
=
a)
1 1
R
6 4
< <
b)
1 2
R
3 5
< <
c)
3 1
R
7 2
< <
d)
2 4
R
3 5
< <
e)
4 9
R
5 10
< <
07. (Efomm 2020) Seja a esfera de raio R inscrita na pirâmide quadrangular regular de aresta base 2 cm e aresta lateral
38 cm. Sabendo-se que a esfera tangencia todas as faces da pirâmide, o valor de R, em cm, é
a)
37 1
6
+
b)
39 1
38
−
c)
6 38 12
17
+
d)
37 1
6
−
e)
6 38 12
17
−

3. EFOOM 2020
3
08. (Efomm 2020) A inequação | x | | 2x 8 | | x 8 |
+ − ≤ + é satisfeita por um número de valores inteiros de x igual a
a) 5
b) 6
c) 7
d) 8
e) 9
09. (Efomm 2020) Considere a inequação ( )
7 4 2 2
x x x 1 x 4x 3 x 7x 54 0.
− + − − + − − ≤ Seja I o conjunto dos números
inteiros que satisfaz a desigualdade e n a quantidade de elementos de I. Com relação a n, podemos afirmar que
a) n é um número primo.
b) n é divisível por 7.
c) n não divide 53904.
d) n é um quadrado perfeito.
e) n é divisível por 6.
10. (Efomm 2020) Seja ABC um triângulo inscrito em uma circunferência de centro O. Sejam O' e E o incentro do
triângulo ABC e o ponto médio do arco BC que não contém o ponto A, respectivamente. Assinale a opção que apresenta
a relação entre os segmentos EB, EO' e EC.
a) EB EO' EC
= =
b) EB EO' EC
< =
c) EB EO' EC
> >
d) EB EO' EC
= >
e) EB EO' EC
< <
11. (Efomm 2020) Sejam a circunferência 1
C , com centro em A e raio 1, e a circunferência 2
C , que passa por A, com
centro em B e raio 2. Sabendo-se que D é o ponto médio do segmento AB, E é um dos pontos de interseção entre 1
C
e 2
C , e F é a interseção da reta ED com a circunferência 2
C , o valor da área do triângulo AEF, em unidades de área é
a)
15
2
8
+
b)
15
1
4
+
c)
3 15
8
d)
15
4
e)
5 15
8

4. EFOOM 2020
4
12. (Efomm 2020) Seja o somatório
2020
j
j 0
S i
=
= ∑ , onde i é a unidade imaginária. Sobre o valor de S, é correto afirmar que
a) S 1 i
= −
b) S 1 i
= +
c) S 1
=
d) S i
=
e) 3
S i
=
13. (Efomm 2020) Seja a matriz A
1 1 1 1 1
1 2 3 4 5
1 4 9 16 25
1 8 27 64 125
1 16 81 256 625
. Qual é o valor do determinante da matriz A?
a) 96
b) 98
c) 100
d) 144
e) 288
14. (Efomm 2020) Sejam os números reais a e b tais que
3
x 0
ax b 2 7
lim
x 12
→
+ −
= . O valor do produto a b
⋅ é
a) 52
b) 56
c) 63
d) 70
e) 84

5. EFOOM 2020
5
15. (Efomm 2020) Seja f uma função real definida por
2
x ; se x 2
f(x) ax b; se 2 x 2
2x 6; se 2 x
 ≤ −


= + − < <

 − ≤


, com 𝑎𝑎, 𝑏𝑏 ∈ ℝ. Sabendo que os limites
x 2
lim f(x)
→+
e
x 2
lim f(x)
→−
existem, assinale a opção que apresenta | a b | .
+
a)
1
6
b)
1
5
c)
1
4
d)
1
3
e)
1
2
16. (Efomm 2020) A trombeta de Gabriel é um sólido matemático formado pela rotação da curva
1
y
x
= em torno do eixo
x.
O volume desse sólido no intervalo 1 x 10
≤ ≤ é
a) V ln(10)
=
b)
9
V
10
π
=
c)
9
V
5
π
=
d) V ln(10)
π
=
e) V 8π
=

6. EFOOM 2020
6
17. (Efomm 2020) Uma parte do gráfico da função f está representado na figura abaixo. Assinale a alternativa que pode
representar f(x).
a) f(x) sen(x ) 1
π
= − +
b) f(x) 2sen x 1
2
π
 
= − +
 
 
c) f(x) sen 2x 2
6
π
 
= − +
 
 
d) f(x) 2sen(2x) 1
= +
e) f(x) 2sen 2x 1
6
π
 
= − +
 
 
18. (Efomm 2020) Sejam u, v
 
e w

vetores do ℝ3
. Sabe-se que u v w 0,
+ + =

   1
| v | ,
2
=
 3
| u |
2
=

e | w | 2.
=

Assinale a opção
que apresenta o valor de u v v w u w.
⋅ + ⋅ + ⋅
     
a)
3
7
b)
13
4
−
c)
7
16
−
d)
5
8
e)
4
7

7. EFOOM 2020
7
19. (Efomm 2020) Sejam o plano : 6x 4y 4z 9 0,
α − − + = os pontos A ( 1; 3; 2)
= − e B (m; n; p).
= Sabendo-se que o ponto
B é simétrico ao ponto A, em relação ao plano ,
α o valor da soma m n p
+ + é
a) 2
−
b) 0
c)
1
4
d)
7
4
e) 3

8. EFOOM 2020
8
GABARITO
1 - A 2 - D 3 - A 4 - ANULADA 5 - C
6 - B 7 - D 8 - E 9 - D 10 - A
11 - C 12 - C 13 - E 14 - B 15 - E
16 - B 17 - E 18 - B 19 - E