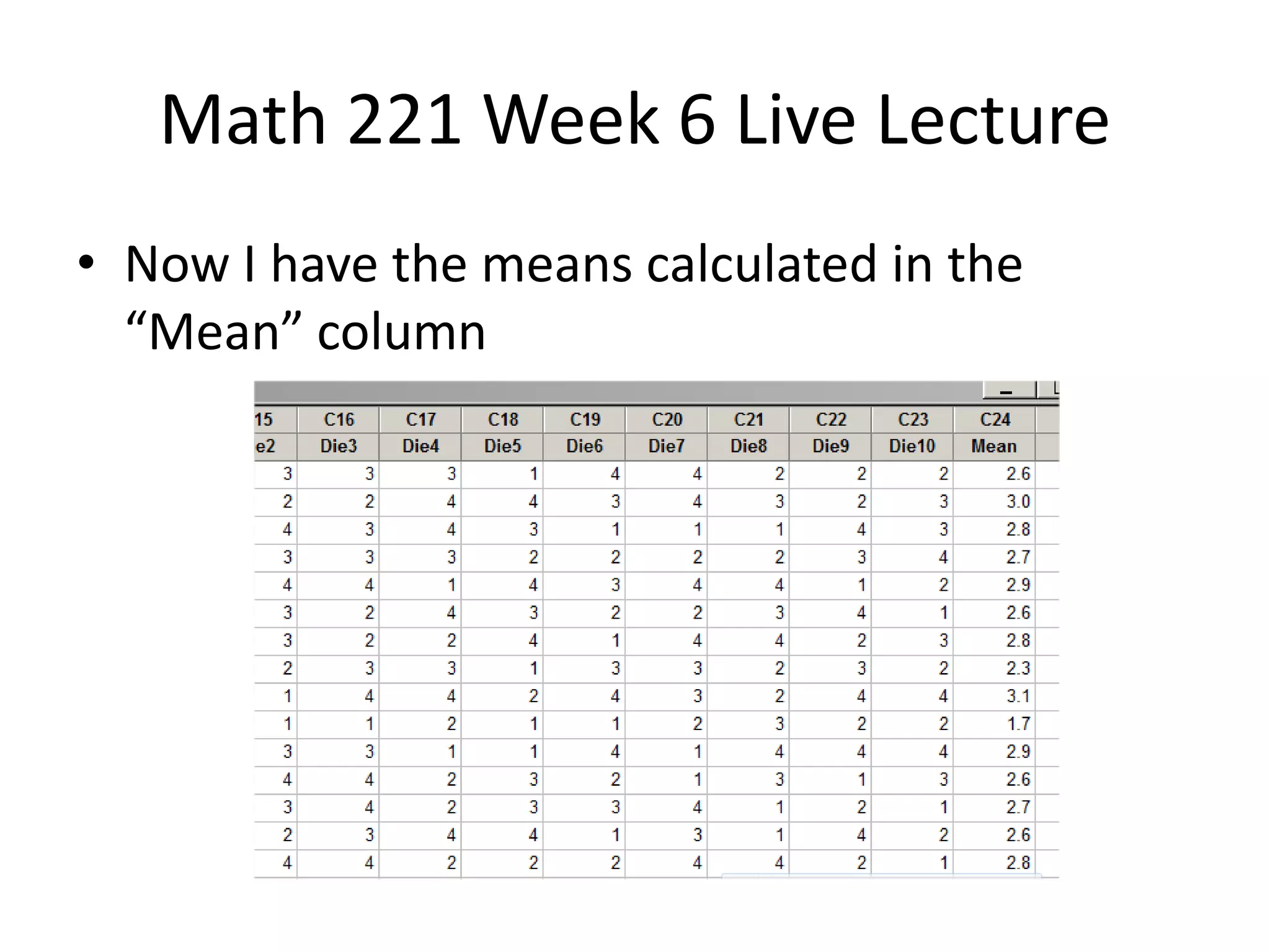
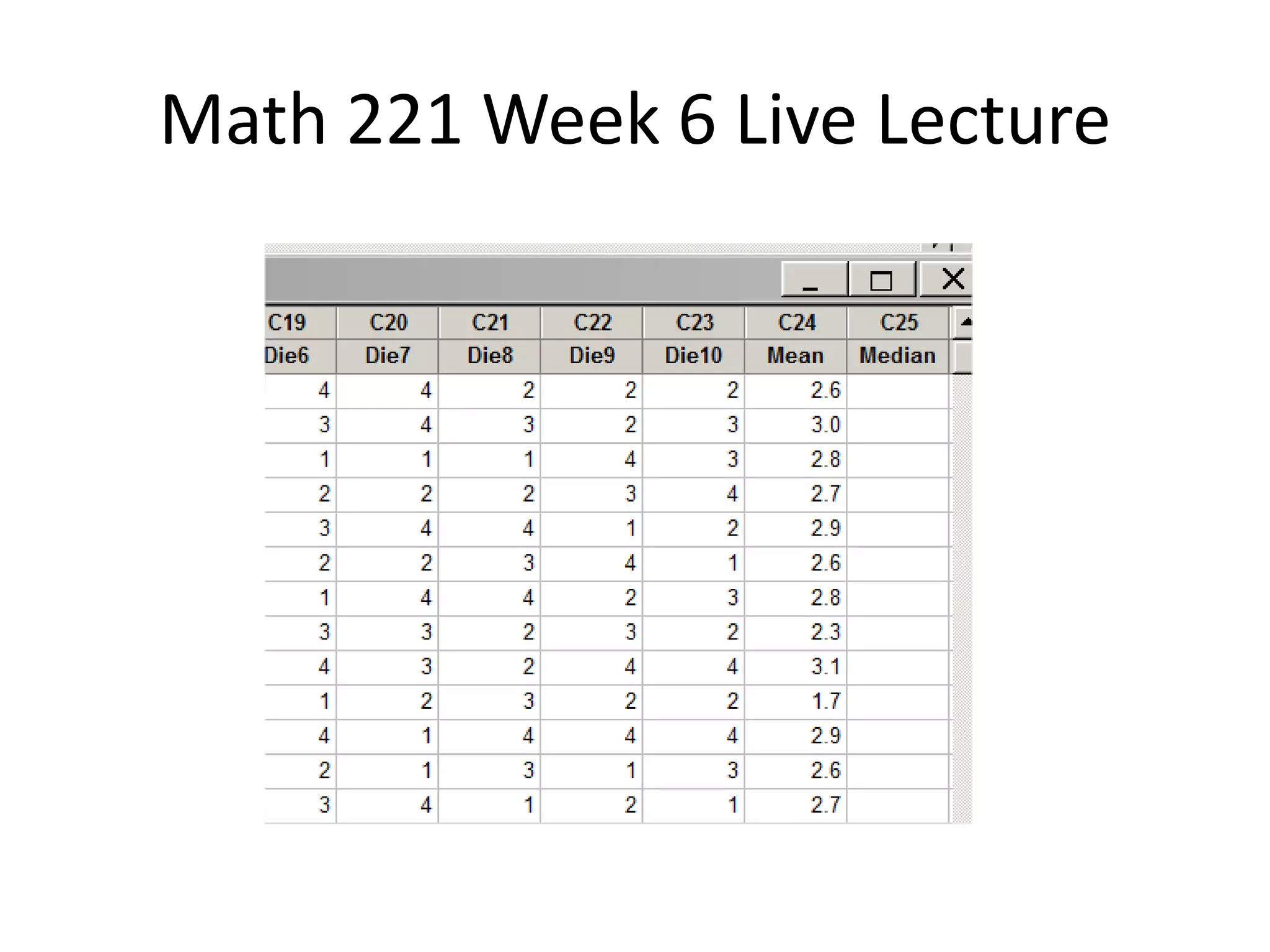
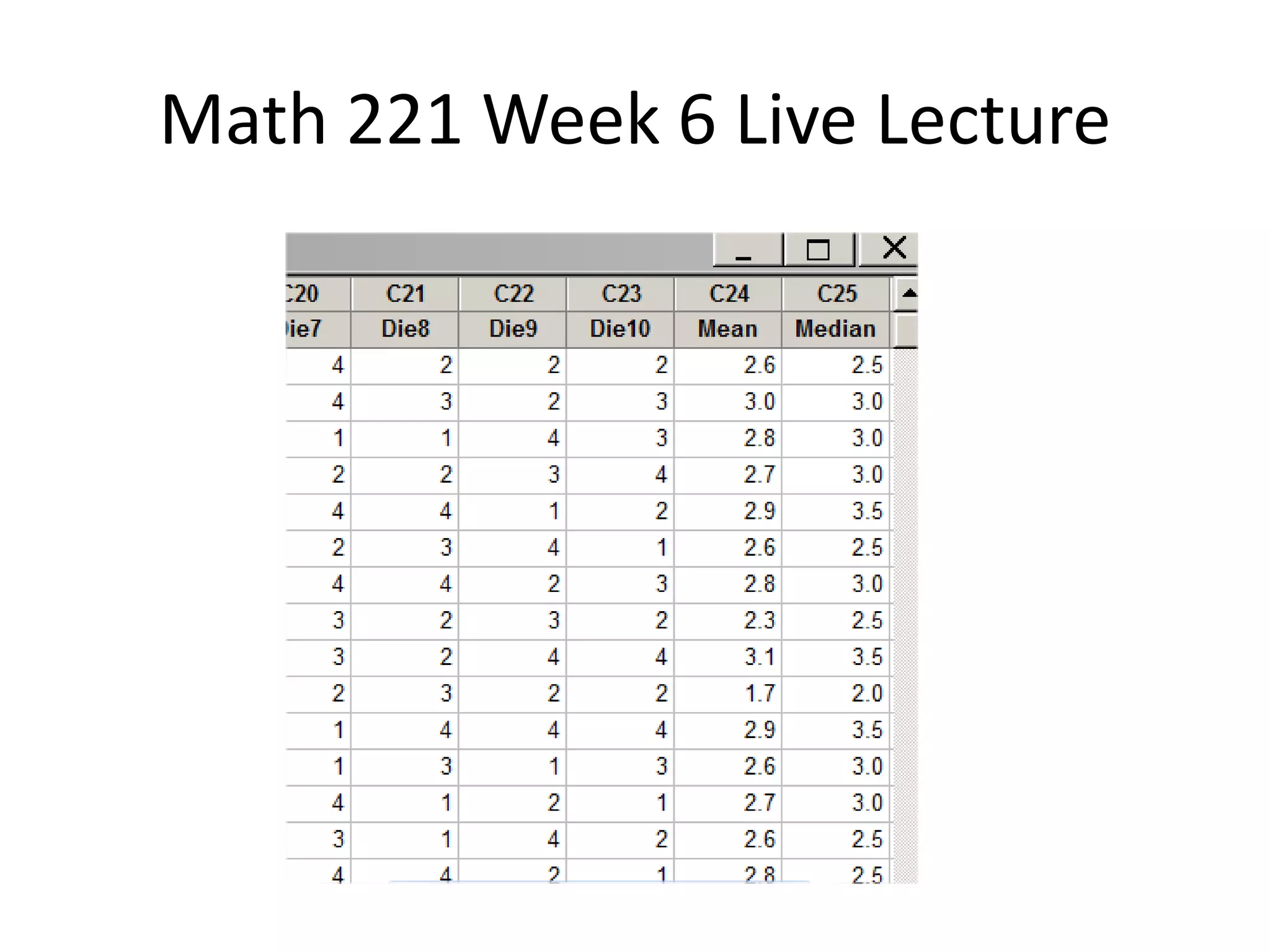
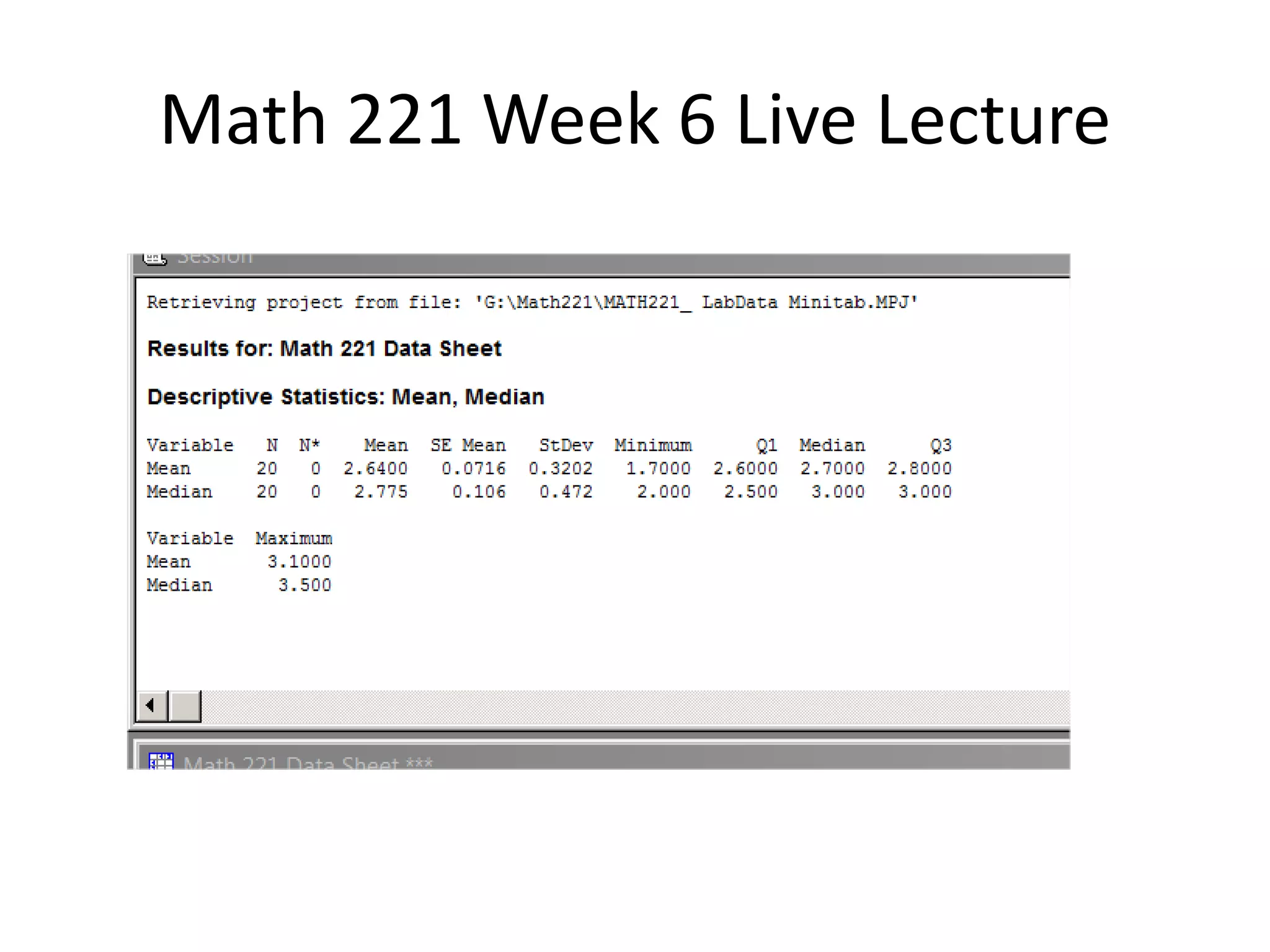
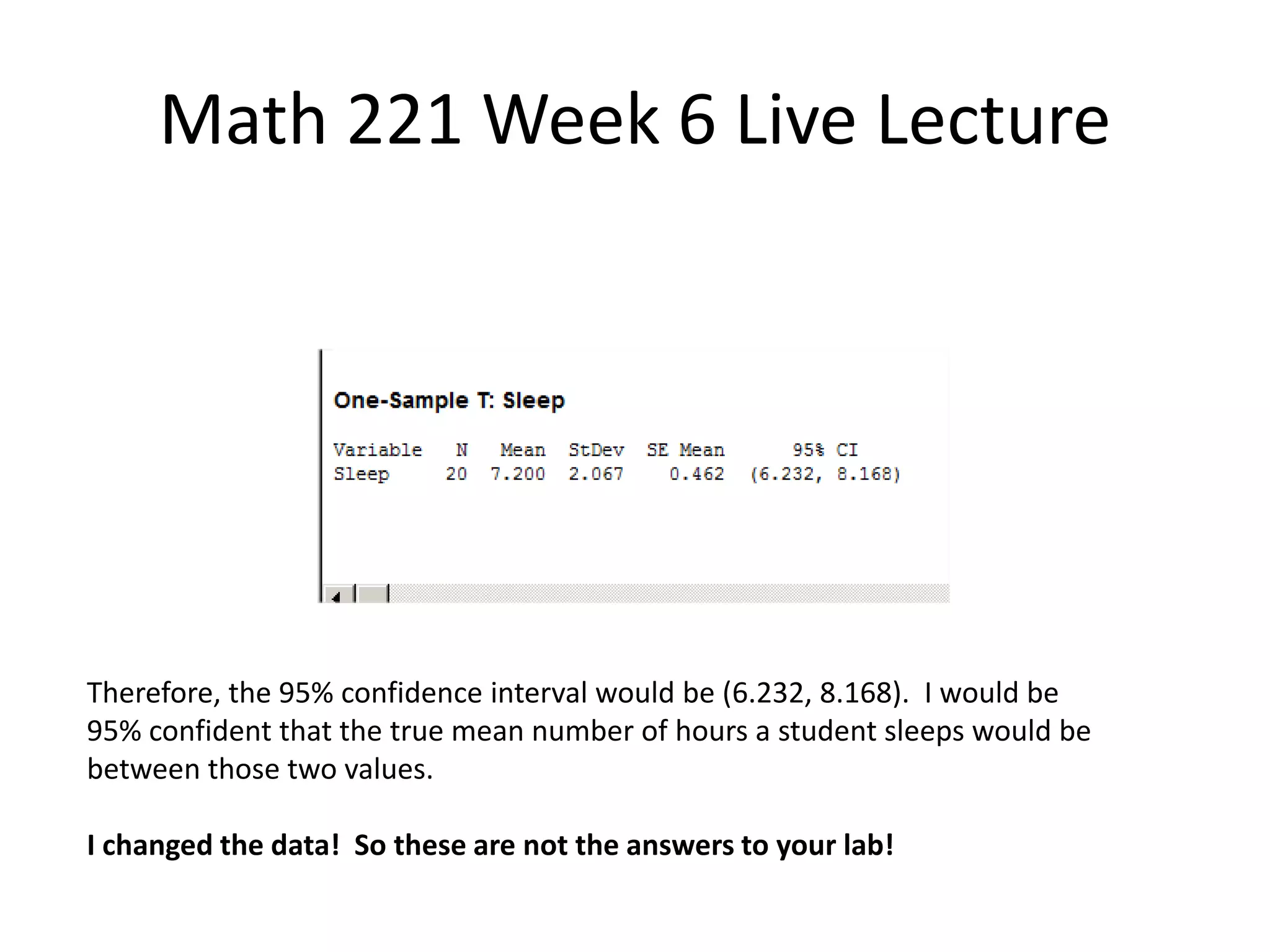
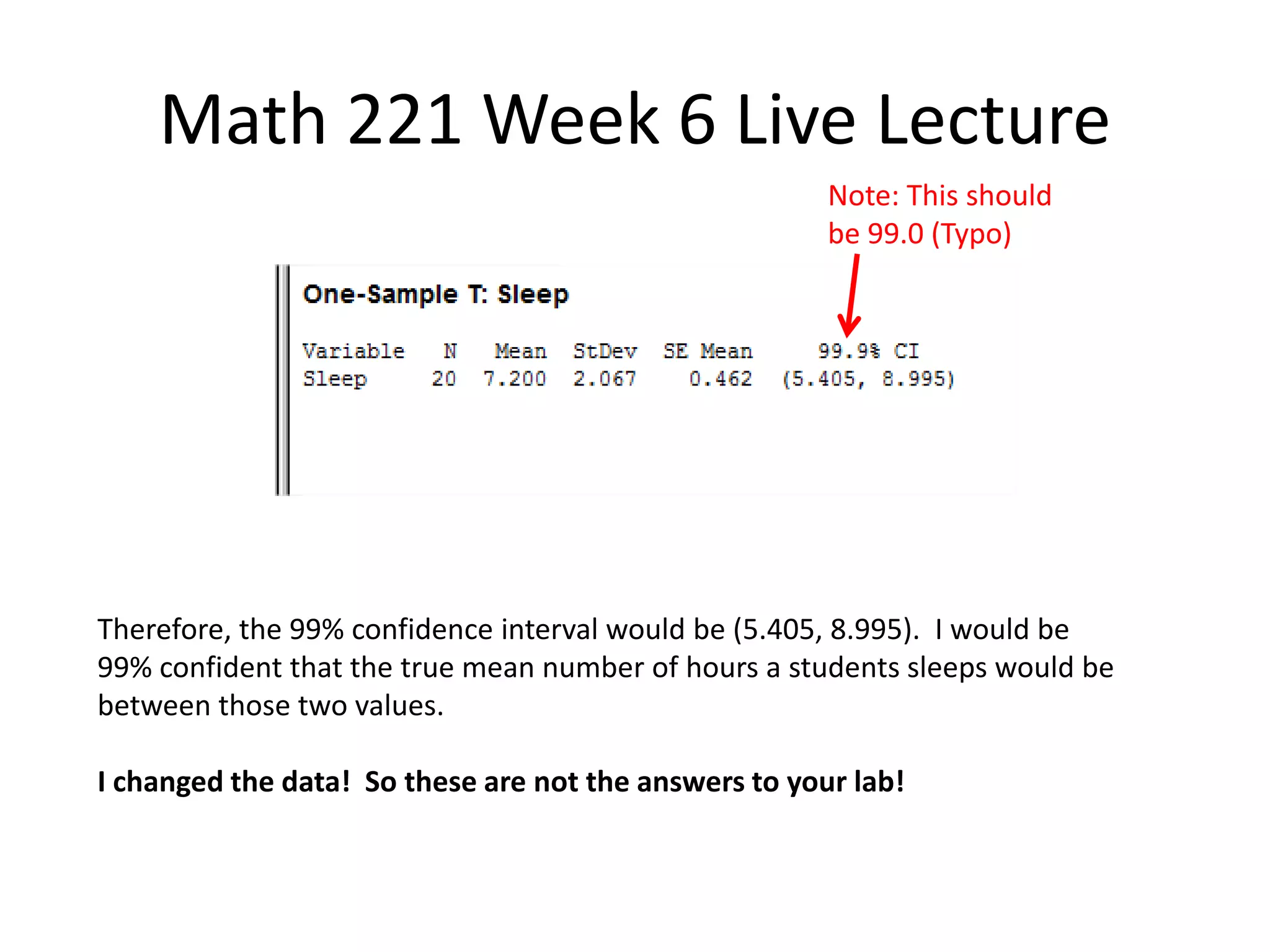
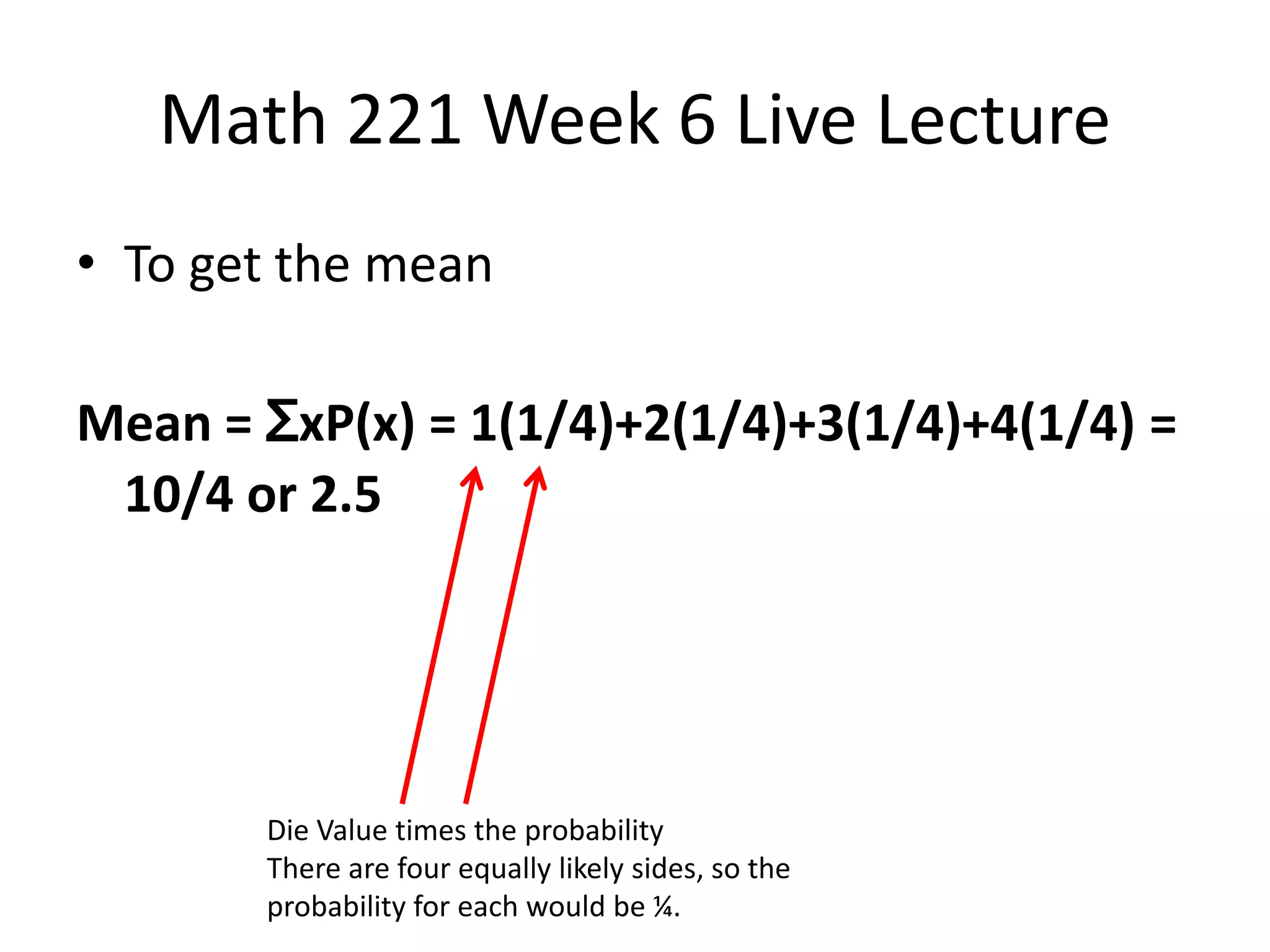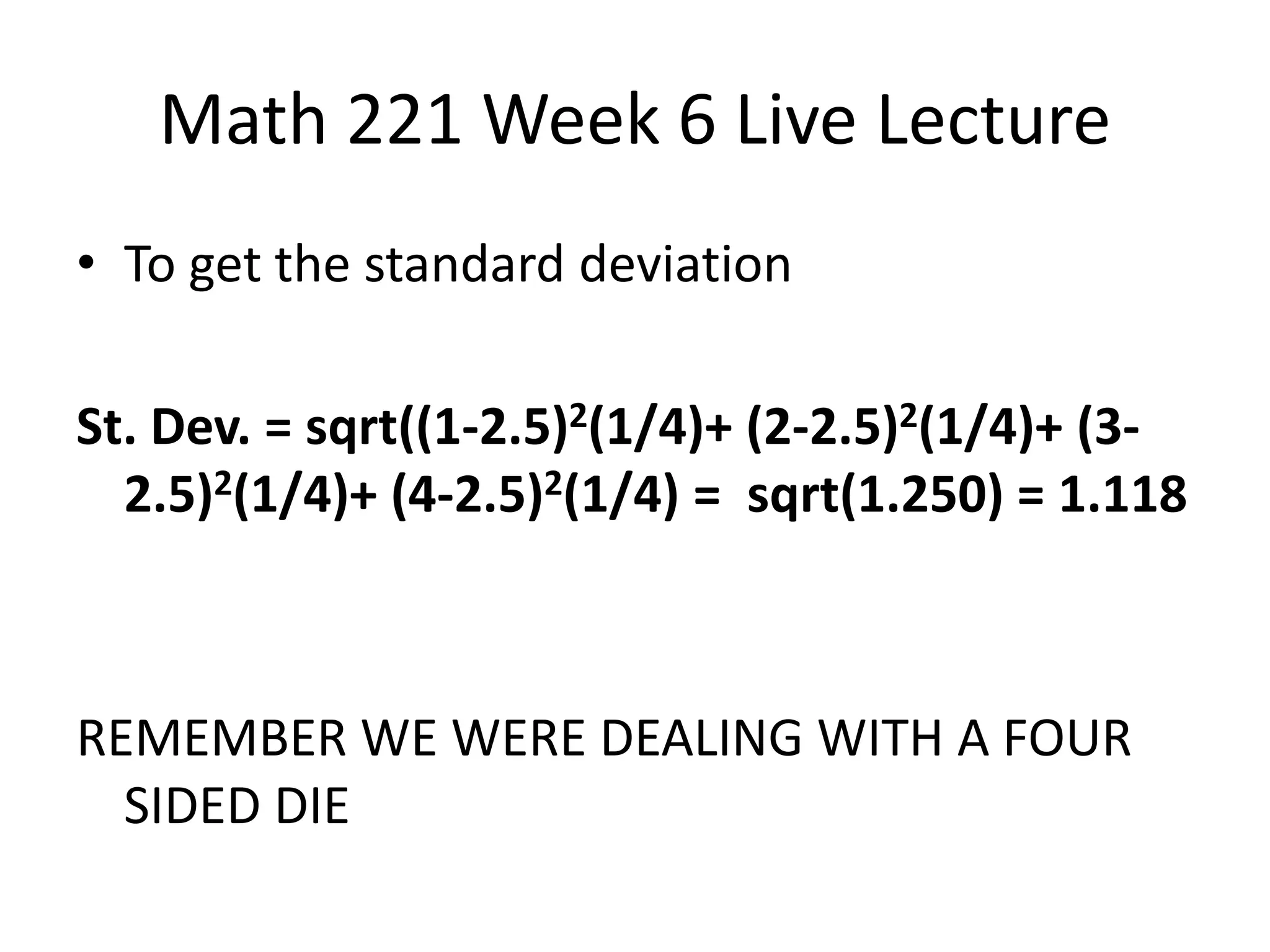This document contains a transcript of a live lecture for a Math 221 class. The lecture covered examples for the Week 6 lab, including calculating the mean and standard deviation of rolling a four-sided die. It also discussed finding the mean and median of 10 die rolls and comparing their variability. Confidence intervals for student sleep hours were computed at the 95% and 99% levels. The 99% interval was wider due to requiring a higher level of certainty about the estimated mean value.