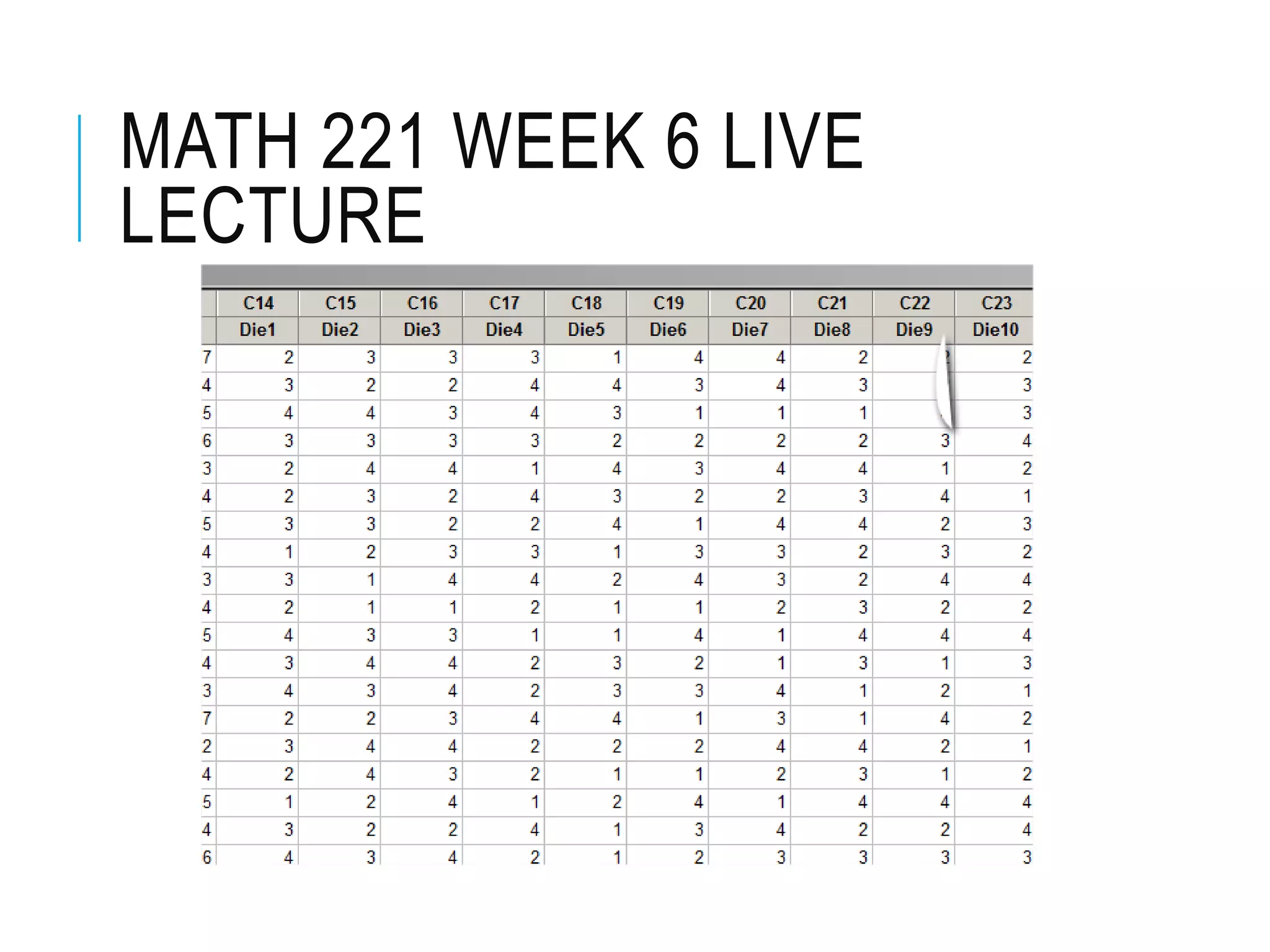
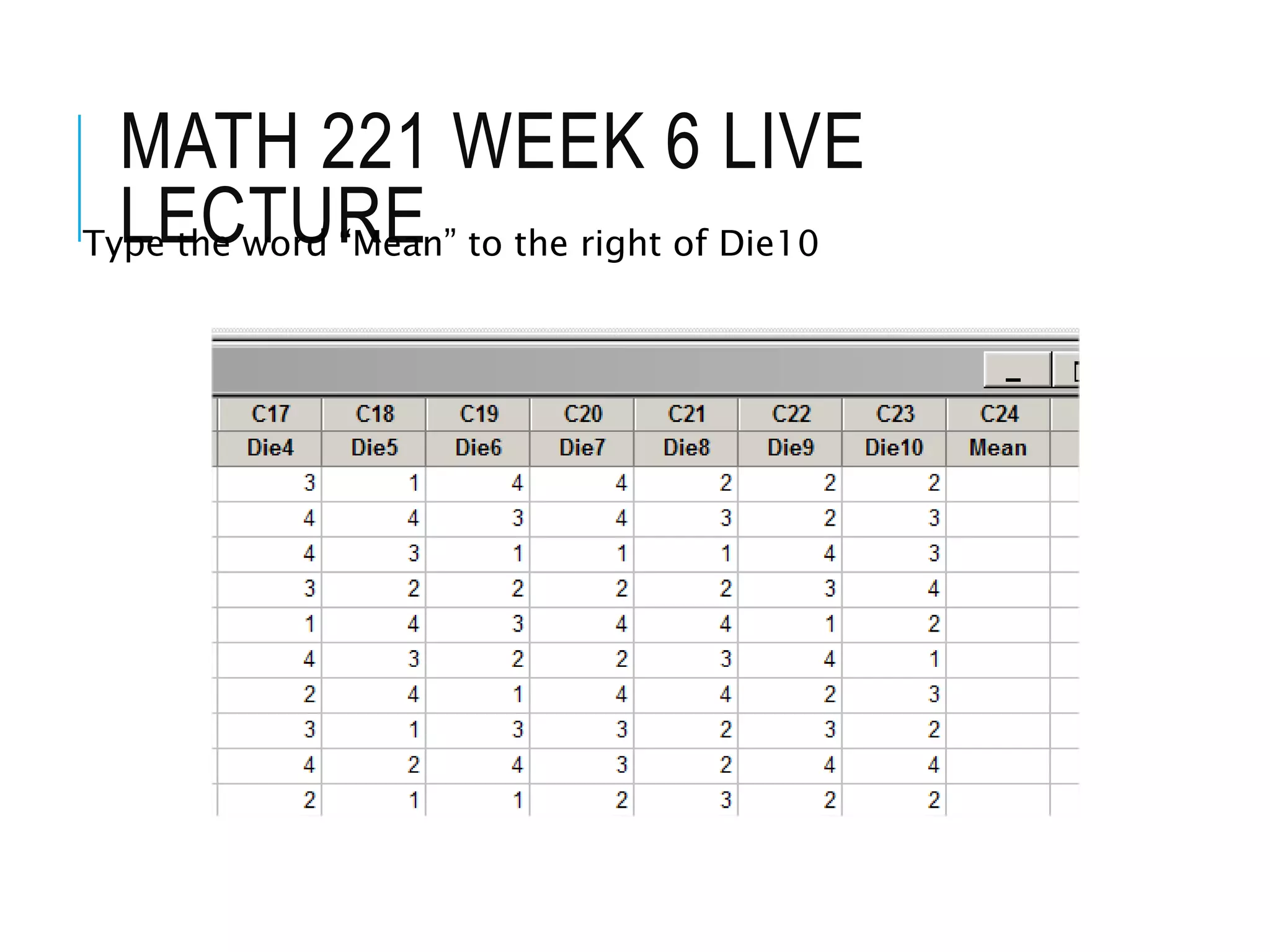
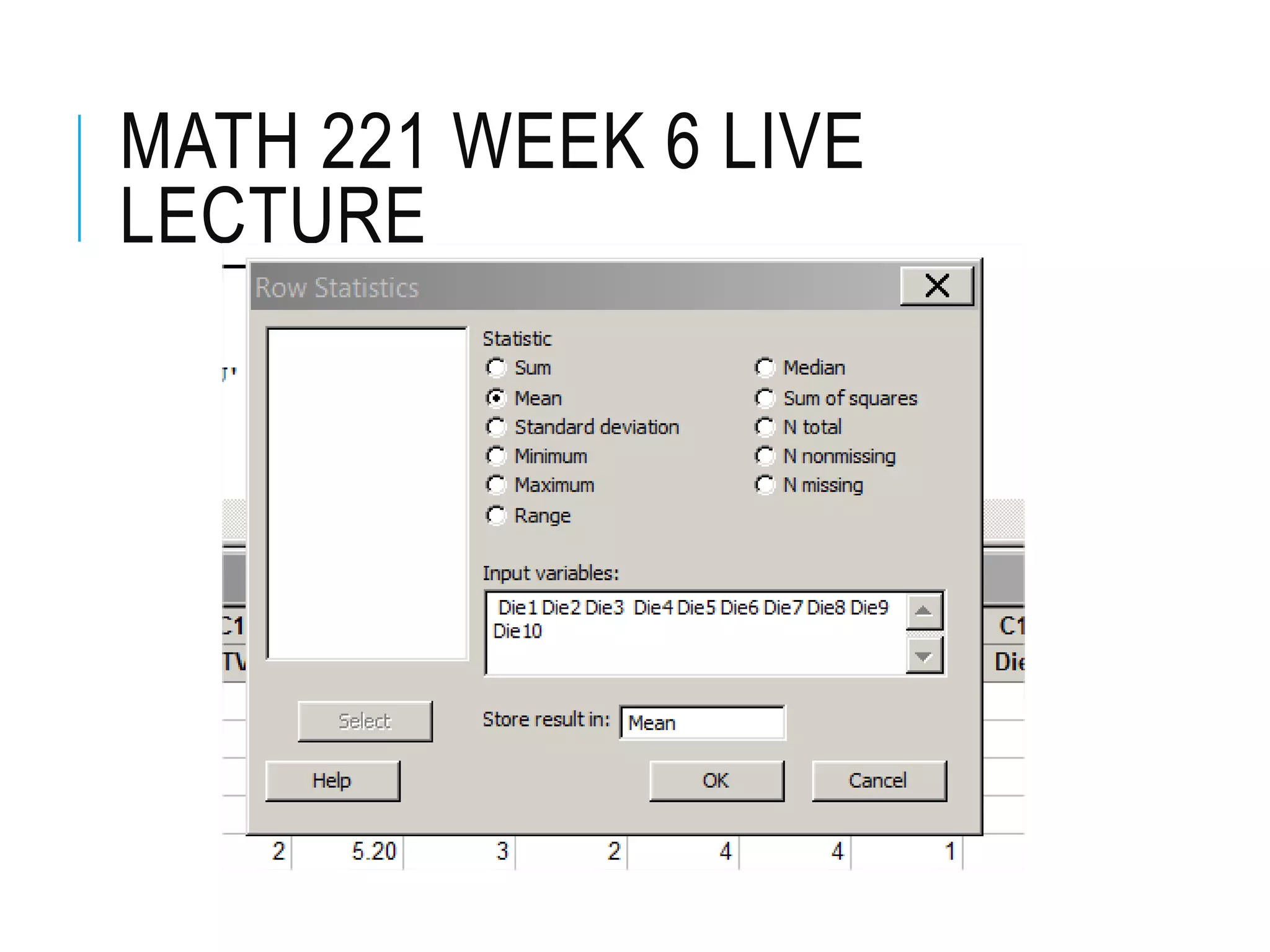
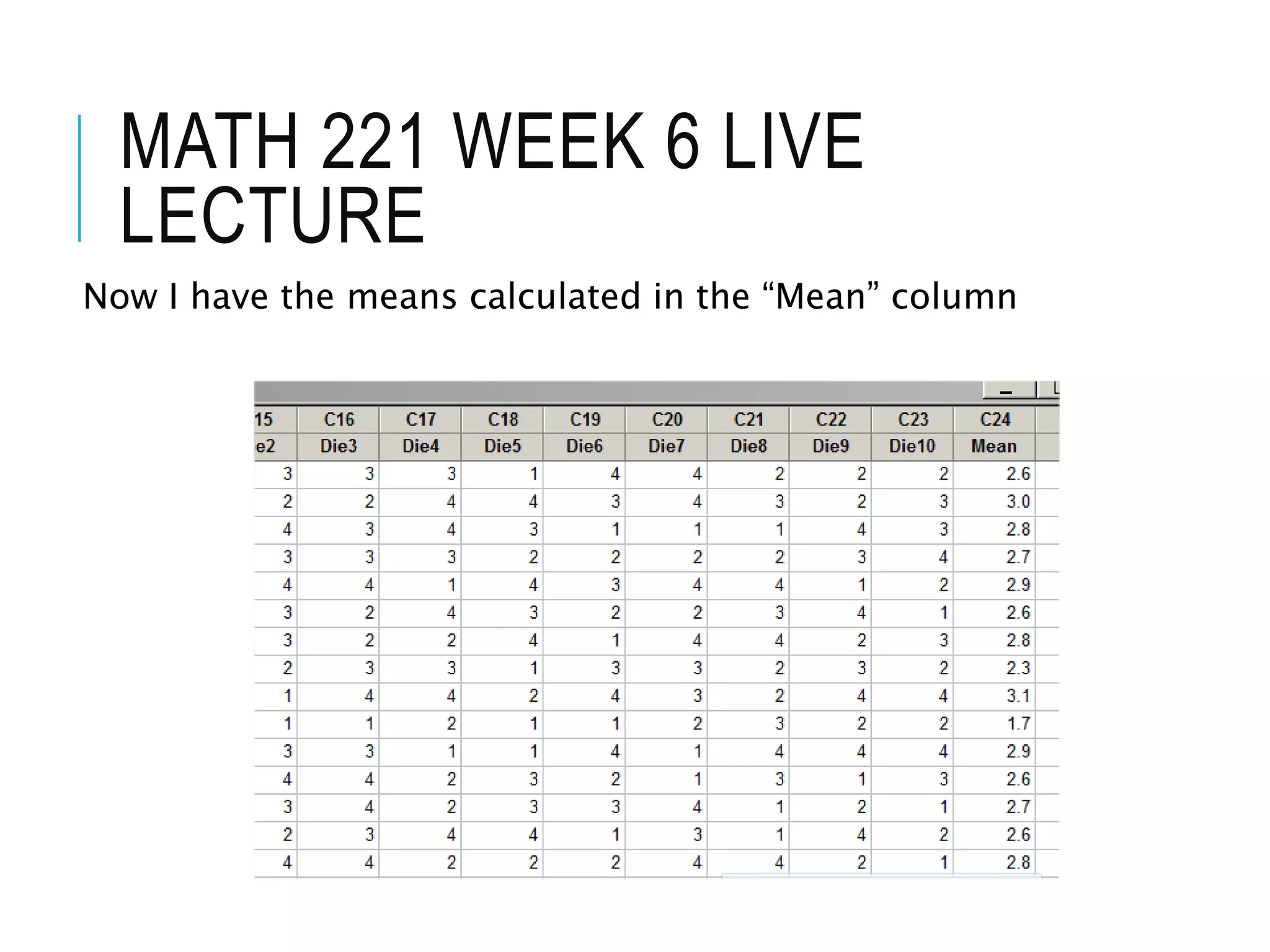
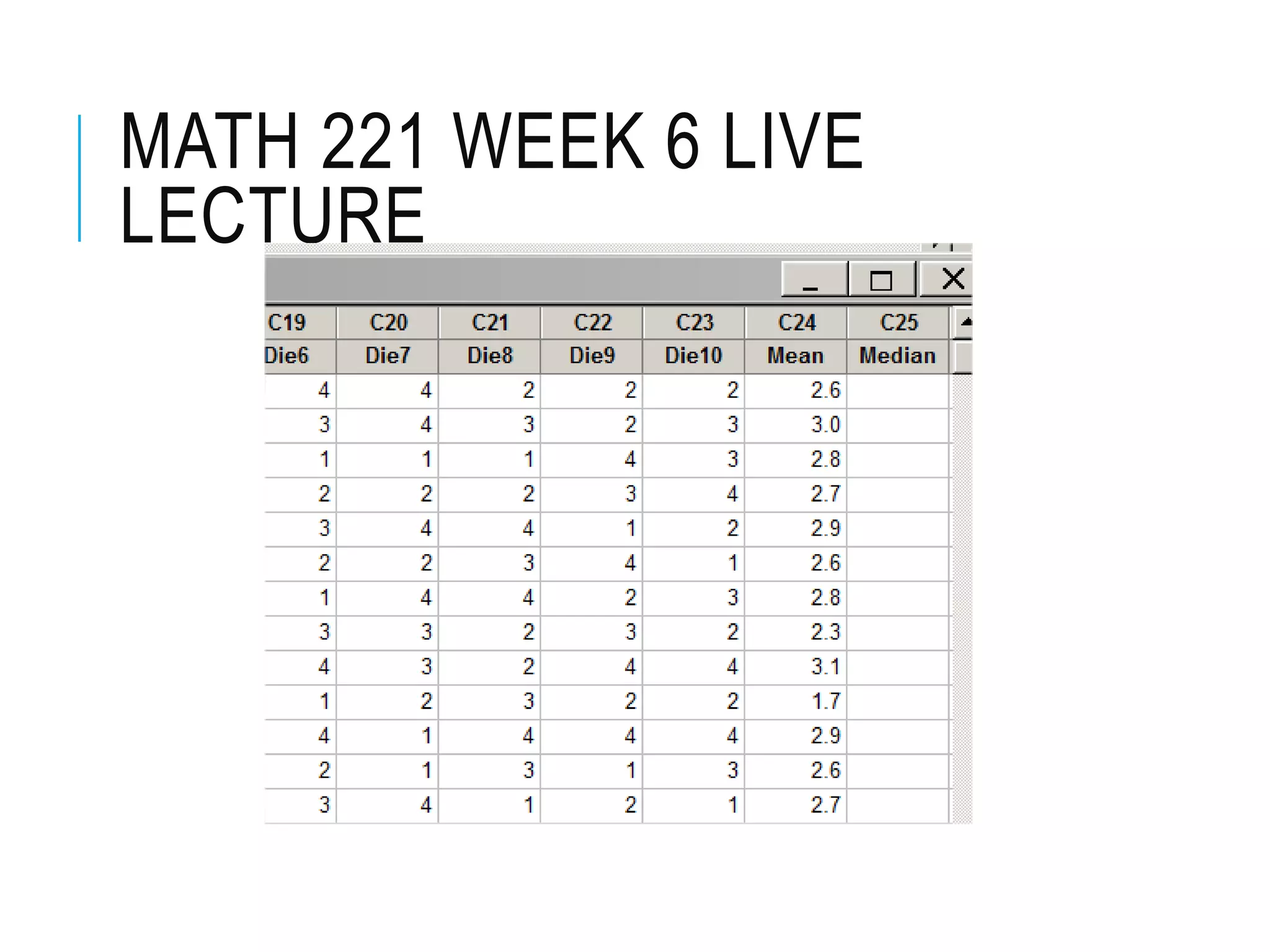
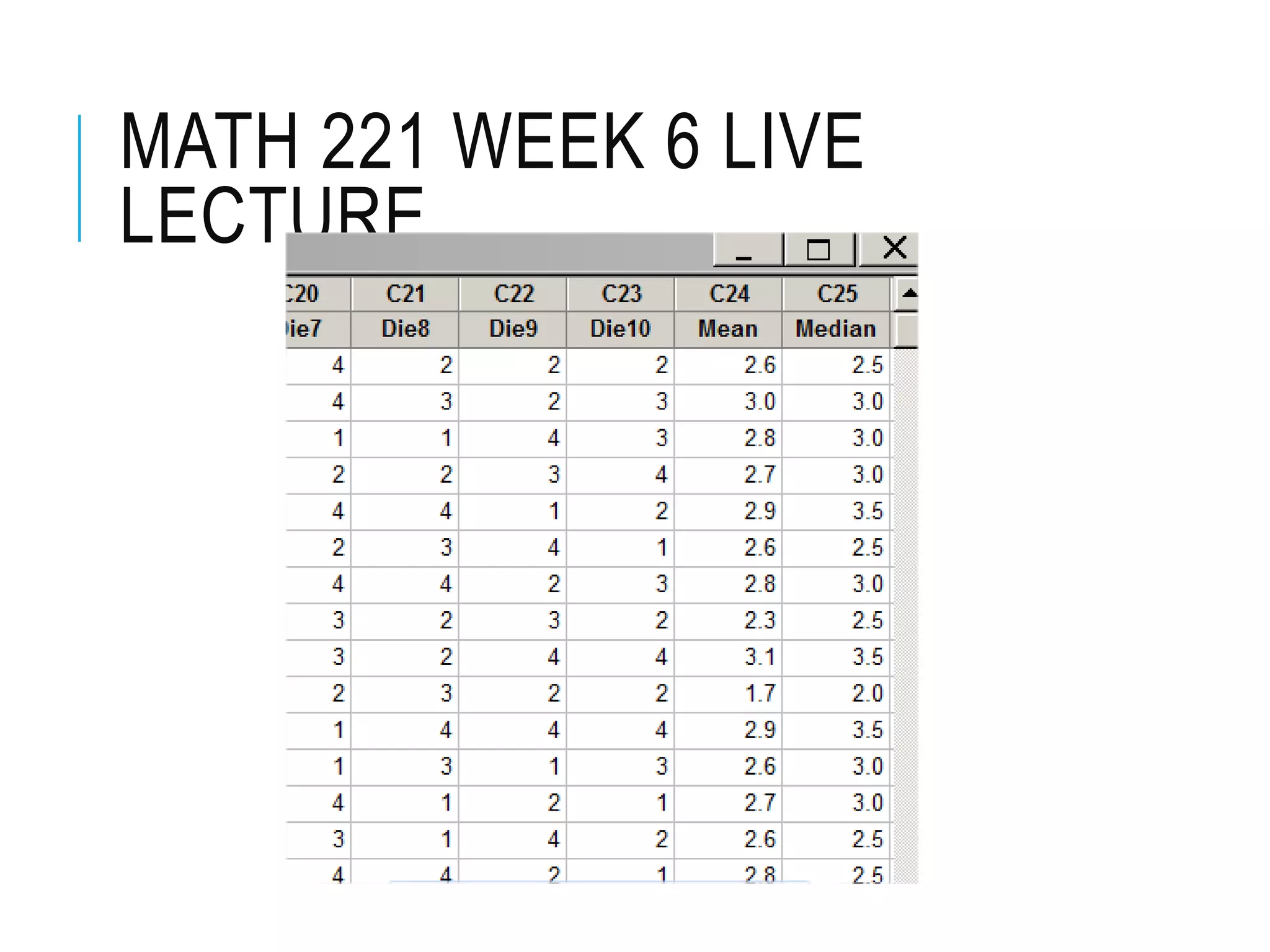
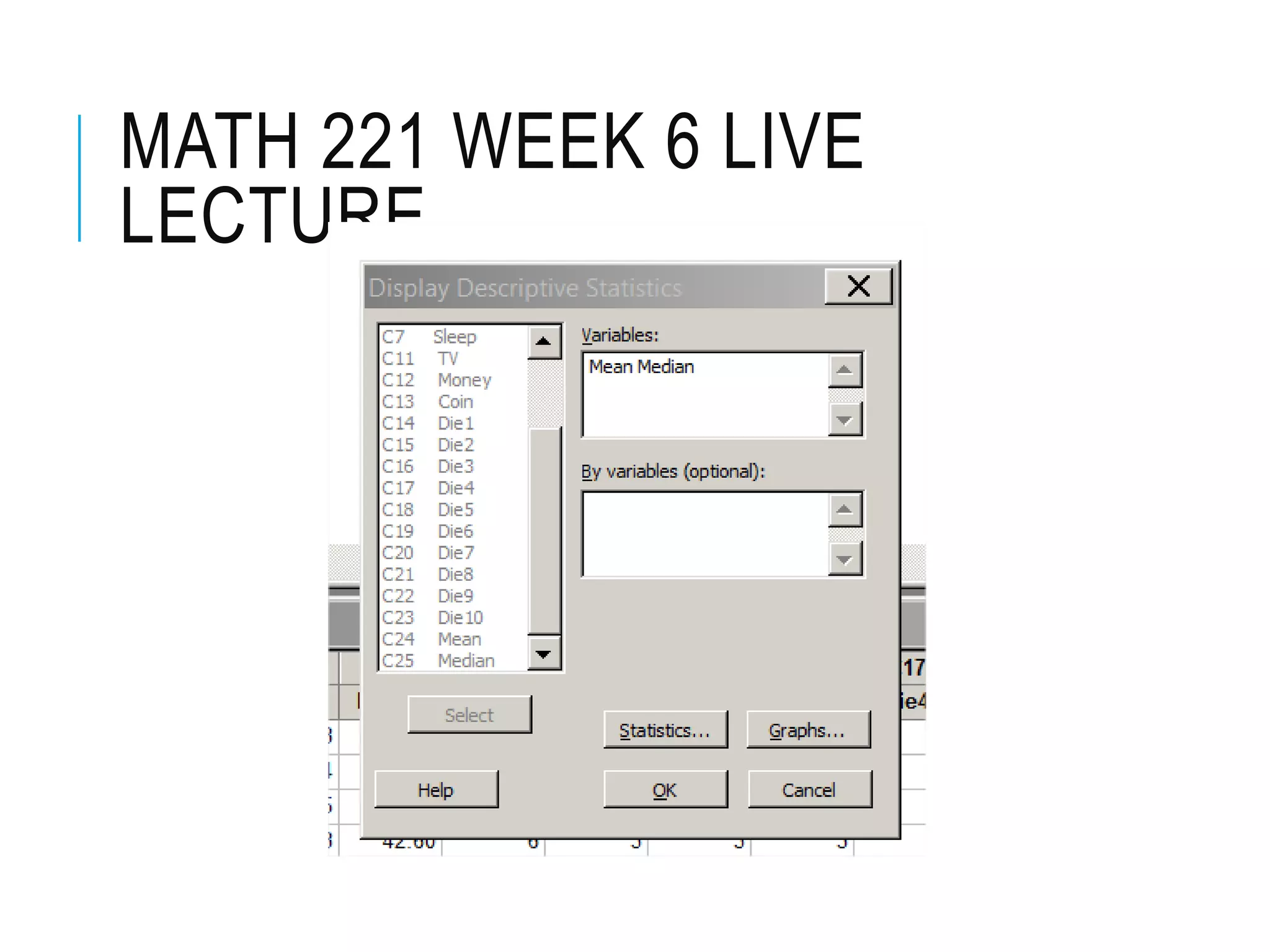
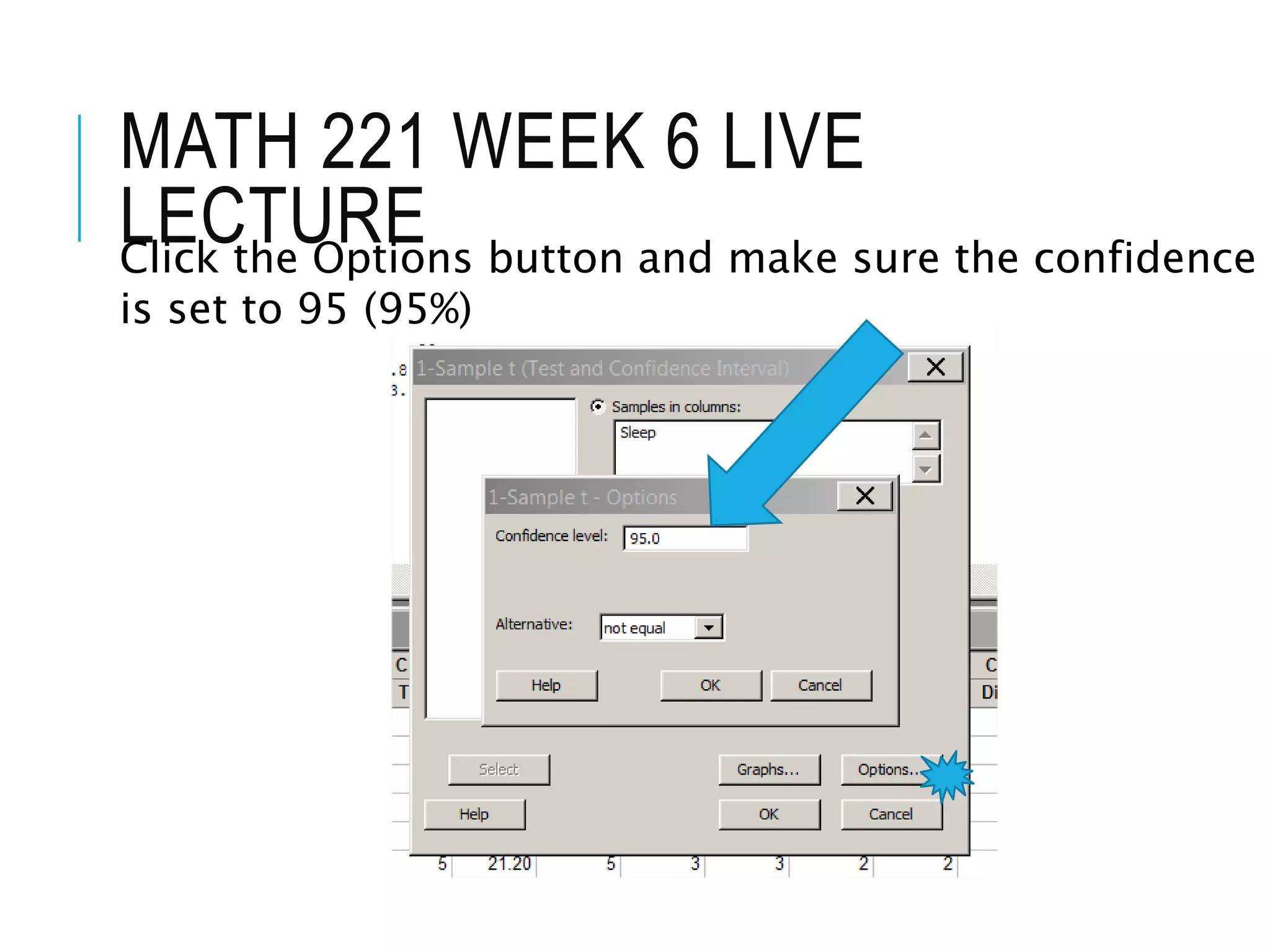
This document contains the notes from a statistics lecture. It discusses key concepts like discrete and continuous random variables. It works through examples of calculating the mean and standard deviation of rolling a four-sided die. It has students calculate descriptive statistics like means, medians, and confidence intervals from sample die roll data. The document explains that increasing the confidence level from 95% to 99% widens the confidence interval, as more certainty requires considering a broader range of possible values.