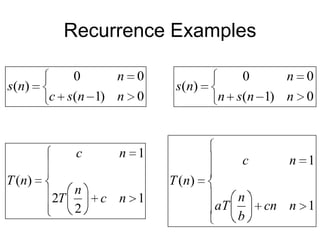
The document discusses recurrence relations and the Master Theorem for solving recurrences that arise from divide-and-conquer algorithms. It introduces recurrence relations and examples. It then explains the substitution method, iteration method, and Master Theorem for solving recurrences. The Master Theorem provides a "cookbook" for determining the running time of a divide-and-conquer algorithm where the problem of size n is divided into a subproblems of size n/b and the cost is f(n). It presents the three cases of the Master Theorem and works through examples of its application.

1. Solving Recurrences
The Master Theorem

2. Recurrence Relations

3. Recurrences
• The expression:
c
T ( n)
n 1
n
2T
2
cn n 1
is a recurrence.
– Recurrence: an equation that describes a function in
terms of its value on smaller functions

4. Recurrence Examples
s(n)
0
c s(n 1) n 0
c
T ( n)
n 0
n
2T
2
s(n)
n 1
0
n 0
n s(n 1) n 0
c
n 1
n
aT
b
cn n 1
T ( n)
c n 1

5. Solving Recurrences
• Substitution method
• Iteration method
• Master method

6. Solving Recurrences
• The substitution method (CLR 4.1)
– “Making a good guess” method
– Guess the form of the answer, then use
induction to find the constants and show that
solution works
– Examples:
• T(n) = 2T(n/2) + (n)  T(n) =
• T(n) = 2T( n/2 ) + n  ???
(n lg n)

7. The Master Theorem
• Given: a divide and conquer algorithm
– An algorithm that divides the problem of size
n into a subproblems, each of size n/b
– Let the cost of each stage (i.e., the work to
divide the problem + combine solved
subproblems) be described by the function
f(n)
• Then, the Master Theorem gives us a
cookbook for the algorithm’s running time:

8. The Master Theorem
• if T(n) = aT(n/b) + f(n) then
n log b a
T ( n)
f (n) O n log b a
log b a
log b a
n
f ( n)
log n
f ( n)
n
f ( n)
n log b a AND
af (n / b) cf (n) for large n
0
c 1

9. Using The Master Method
• T(n) = 9T(n/3) + n
– a=9, b=3, f(n) = n
– nlog a = nlog 9 = (n2)
– Since f(n) = O(nlog 9 - ), where =1, case 1
applies:
b
3
3
T ( n)
n
log b a
when f (n) O n
– Thus the solution is T(n) =
(n2)
log b a

10. Simplified Masters Theorem
nd
T ( n)
d
if (a b d )
d
n log n
if (a b )
n log ba log n
if (a b d )

11. • In divide and conquer generally, a problem
instance size of n is divided into two instances of
n/2. More generally an instance of size n can be
divided into b instances of size n/b, with 'a' of the
needing to be solved. ( hence, 'a' and b are
constants; a>=1 and b>1). Assuming that size n
is a power of b, by simplifying the analysis, the
recurrence for the running time
»T(n)=aT(n/b)+f(n)
• Where f(n) is a function that accounts for the time
spent on dividing the problem into smaller ones
and on combining their solutions.

12. More Examples of Master’s
Theorem
•
•
•
•
•
T(n) = 3T(n/5) + n
T(n) = 2T(n/2) + n
T(n) = 2T(n/2) + 1
T(n) = T(n/2) + n
T(n) = T(n/2) + 1

13. When Master’s Theorem cannot
be applied
• T(n) = 2T(n/2) + n logn
• T(n) = 2T(n/2) + n/ logn