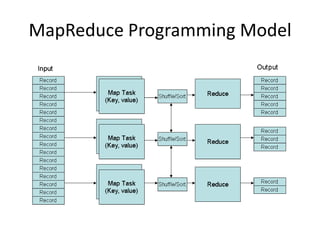
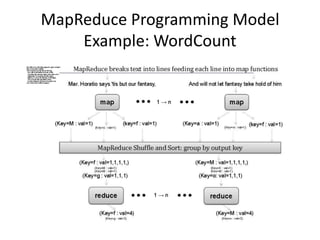
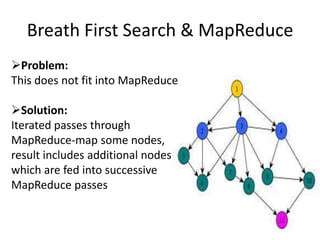
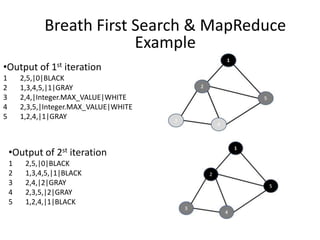
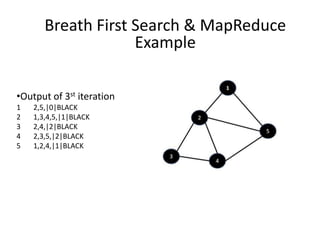
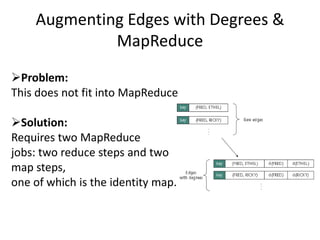
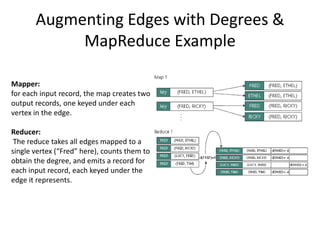
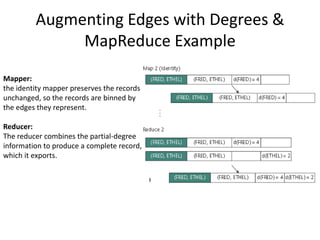
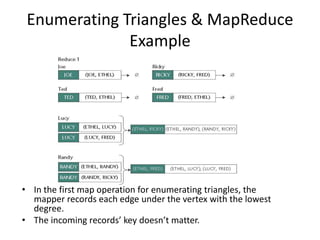
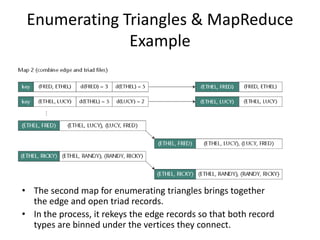
This document discusses using the MapReduce programming model to solve graph problems. It begins with an introduction to MapReduce, describing its history and programming model. It then provides examples of using MapReduce to solve specific graph algorithms, including breath first search, augmenting edges with degree counts, and enumerating triangles. The examples show how graph problems that don't initially seem to fit the MapReduce model can be solved through multiple MapReduce passes that iteratively process more of the graph.

1. MapReduce Programming Model
To Solve Graph Problems
Presented By:
Nishant Gandhi
M.Tech. - CSE 1st Year
1311CS05
Guided By:
Dr. Rajiv Misra

2. Seminar Overview
• Introduction to MapReduce
• MapReduce Programming Model
– Word Count problem
• Graph Problems & MapReduce
– Breath First Search
– Augmenting Edges with Degree
– Enumerating Triangles from Graph

3. Introduction to MapReduce
• History of Computing
– Moore’s Law
• Not holding since last few years
• Memory is still bottle neck for large GHZ processor
– Distributed Problems
• Indexing The Web, Simulating Internet Sized Network, Speeding Up
Content Delivery, Rendering Multiple Frames
– Parallel Computing (1975-1985)
• Synchronization Problems
• Very Costly Super Computers
– Distributed Computing (1995-Today)
• Cost Effective Solution
• Use Commodity Hardware
• Google has no Super Computer

4. Introduction to MapReduce
• History of MapReduce at Google
– Problem at Google
• Computing Large Amount of Data on DS
• Parallelize Computing, Distribute Data, Handle Failure
– One Solution
• New Abstract that allows simple computation & hide
all other mess
• Automatics Parallelization, Distribution, Fault Handling
• MapReduce Paper 2004

5. MapReduce Programming Model
• Motivation
– Automatic Parallelization & Distribution
– Fault tolerant
– Provides Status & Monitoring Tool
– Clean Abstract For Programmer

6. MapReduce Programming Model
• Programming Model
– Borrows From Functional Programming
– User Implement interface of two functions
• Map & Reduce
• map (in_key, in_value) --> (out_key, intermediate_value)
list
• reduce (out_key, intermediate_value list) --> out_value list

7. MapReduce Programming Model
map: (K1,V1) → list (K2,V2)
reduce: (K2,list(V2)) → list (K3,V3)
1. Map function is applied to every input key-value pair
2. Map function generates intermediate key-value pairs
3. Intermediate key-values are sorted and grouped by key
4. Reduce is applied to sorted and grouped intermediate
key-values
5. Reduce emits result key-values

8. MapReduce Programming Model

9. MapReduce Programming Model
Example: WordCount

10. Graph Problems
Graphs are ubiquitous in modern society. Some
examples:
• The hyperlink structure of the web
• Social networks on social networking sites like
Facebook, IMDB, email, text messages and tweet
flows (like Twitter)
• Transportation networks (roads, trains, fights etc)
• Human body can be seen as a graph of genes,
proteins, cells etc..

11. Graph Problems & MapReduce
• Performing Computation on a graph data
structure requires processing at each node
• Each node contain node-specific data as well
as links (edges) to other nodes
• Computation must traverse the graph and
perform the computation step
• How do we traverse a graph in MapReduce?
How do we represent the graph for this?

12. Breath First Search & MapReduce
Problem:
This does not fit into MapReduce
Solution:
Iterated passes through
MapReduce-map some nodes,
result includes additional nodes
which are fed into successive
MapReduce passes

13. Breath First Search & MapReduce
Example
Representation as adjacent list
ID EDGES|DISTANCE_FROM_SOURCE|COLOR|
• Input to MAP
1 2,5|0|GRAY|
2 1,3,4,5|Integer.MAX_VALUE|WHITE|
3 2,4|Integer.MAX_VALUE|WHITE|
4 2,3,5|Integer.MAX_VALUE|WHITE|
5 1,2,4|Integer.MAX_VALUE|WHITE|

14. Breath First Search & MapReduce
Example
• 1st iteration of Map
1 2,5|0|BLACK|
2 NULL|1|GRAY|
5 NULL|1|GRAY|
2 1,3,4,5|Integer.MAX_VALUE|WHITE|
3 2,4|Integer.MAX_VALUE|WHITE|
4 2,3,5|Integer.MAX_VALUE|WHITE|
5 1,2,4|Integer.MAX_VALUE|WHITE|
•1st iteration for Reduce(result only for node 2)
2 NULL|1|GRAY|
2 1,3,4,5|Integer.MAX_VALUE|WHITE|
The reducers job is to take all
this data and construct a new
node using
the non-null list of edges
the minimum distance
the darkest color

15. Breath First Search & MapReduce
Example
•Output of 1st iteration
1 2,5,|0|BLACK
2 1,3,4,5,|1|GRAY
3 2,4,|Integer.MAX_VALUE|WHITE
4 2,3,5,|Integer.MAX_VALUE|WHITE
5 1,2,4,|1|GRAY
•Output of 2st iteration
1 2,5,|0|BLACK
2 1,3,4,5,|1|BLACK
3 2,4,|2|GRAY
4 2,3,5,|2|GRAY
5 1,2,4,|1|BLACK

16. Breath First Search & MapReduce
Example
•Output of 3st iteration
1 2,5,|0|BLACK
2 1,3,4,5,|1|BLACK
3 2,4,|2|BLACK
4 2,3,5,|2|BLACK
5 1,2,4,|1|BLACK

17. Augmenting Edges with Degrees &
MapReduce
Problem:
This does not fit into MapReduce
Solution:
Requires two MapReduce
jobs: two reduce steps and two
map steps,
one of which is the identity map.

18. Augmenting Edges with Degrees &
MapReduce Example
Mapper:
for each input record, the map creates two
output records, one keyed under each
vertex in the edge.
Reducer:
The reduce takes all edges mapped to a
single vertex (“Fred” here), counts them to
obtain the degree, and emits a record for
each input record, each keyed under the
edge it represents.

19. Augmenting Edges with Degrees &
MapReduce Example
Mapper:
the identity mapper preserves the records
unchanged, so the records are binned by
the edges they represent.
Reducer:
The reducer combines the partial-degree
information to produce a complete record,
which it exports.

20. Enumerating Triangles & MapReduce
Example
 Problem:
Enumerating 3-cycle sub graph
from given graph
 Solution:
• augmenting the edge records
with vertex valence
• two MapReduce jobs

21. Enumerating Triangles & MapReduce
Example
• In the first map operation for enumerating triangles, the
mapper records each edge under the vertex with the lowest
degree.
• The incoming records’ key doesn’t matter.

22. Enumerating Triangles & MapReduce
Example
• In the first map operation for enumerating triangles, the
mapper records each edge under the vertex with the lowest
degree.
• The incoming records’ key doesn’t matter.

23. Enumerating Triangles & MapReduce
Example
• The second map for enumerating triangles brings together
the edge and open triad records.
• In the process, it rekeys the edge records so that both record
types are binned under the vertices they connect.

24. Enumerating Triangles & MapReduce
Example
• In the second reduce, each bin contains at most one edge record
and some number of triad records (perhaps none).
• For every combination of edge record and triad record in a bin, the
reduce emits a triangle record. The output key isn’t significant.

25. Bibliography
1. J. Dean and S. Ghemawat, “MapReduce: Simplified Data Processing on
Large Clusters,” Comm. ACM, vol. 51, no. 1,2008, pp. 107–112.
2. GoogleDevelopers, “Lecture 5: Parallel Graph Algorithms with
MapReduce,” 28 Aug. 2007; http://youtube.com/watch?v=BT-piFBP4fE.
3. Jonathan Cohen, Graph Twiddling in a MapReduce World. Comp. in
Science & Engineering, July/August 2009, 29-41.

26. Thank You