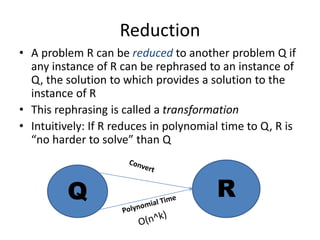
NP-complete problems are problems in NP that are the hardest problems in NP. A problem X is NP-complete if it is in NP and every problem in NP can be quickly transformed into X using a polynomial time reduction. Reduction is the process of rephrasing an instance of one problem as an instance of another problem, such that solving the new instance provides the solution to the original problem. NP-hard problems are at least as hard as the hardest problems in NP and include all NP-complete problems. A problem is NP-hard if all problems in NP can be reduced to it in polynomial time.

1. Topic- NP Complete Problems
Submitted To:-
Mr. Jitendra Gora
Submitted By:-
Nikhil Joshi

2. Contents-
 NP-complete problems
Reduction
NP-Hard

3. NP-complete problems
 What is NP-Complete?
 A problem X that is in NP is also in NP-
Complete if and only if every other problem in
NP can be quickly (i.e. in polynomial time)
transformed into X. In other words:
1. X is in NP (X NP)
2. Every problem in NP is reducible to x

4. Reduction
• A problem R can be reduced to another problem Q if
any instance of R can be rephrased to an instance of
Q, the solution to which provides a solution to the
instance of R
• This rephrasing is called a transformation
• Intuitively: If R reduces in polynomial time to Q, R is
“no harder to solve” than Q
Q R

5. NP-Hard
• What is NP-Hard?
• NP-Hard are problems that are at least as hard
as the hardest problems in NP. Note that NP-
Complete problems are also NP-hard.
However not all NP-hard problems are NP
– If all problems R  NP are polynomial-time
reducible to Q, then Q is NP-Hard
– We say Q is NP-Complete if Q is NP-Hard
and Q  NP

6. • We can say NP-Hard problem Pi when all the
problems of NP Class is to be reduced under
polynomial time.
NP Pi
NP Hard
Polynomial Time

7. NP-Complete
• NP Complete Problems are those Problems
which are reducible to polynomial problem
but the NP-Hard problem which comes Under
NP or resides under NP class .

8. Thank You