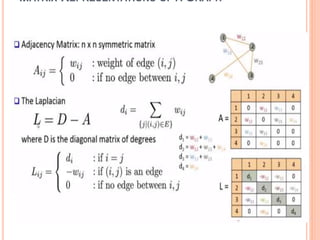
Spectral clustering transforms the clustering problem into a graph-partitioning problem by treating each data point as a graph node. It constructs a similarity graph for all data points and embeds them into a low-dimensional space using the eigenvectors of the graph Laplacian, in which clusters are more obvious. Then a classical clustering algorithm like k-means is applied to partition the embedding. Spectral clustering is flexible and can handle various cluster shapes without assumptions, often outperforming other approaches.