This document presents information on fuzzy arithmetic and operations. It discusses fuzzy numbers, linguistic variables, and arithmetic operations on fuzzy intervals and fuzzy numbers. Some key points: - Fuzzy numbers are fuzzy sets with certain properties like being normal, having closed interval alpha-cuts, and bounded support. - Linguistic variables assign linguistic values like "young" or "old" to numerical variables. They are represented as fuzzy sets. - Arithmetic operations on fuzzy intervals are defined based on the corresponding operations on their alpha-cuts, which are closed intervals. Properties like commutativity and distributivity are discussed. - Operations on fuzzy numbers are similarly defined based on the alpha-cuts of the resulting fuzzy

1. 10/28/2016 1
Guided by
Dr. A G Keskar
Professor
Department of Electronics Engineering
VNIT, Nagpur
Visvesvaraya National Institute Of Technology, Nagpur
Presentation on Fuzzy Arithmetic
Presented By:
LOKESH GAHANE
(MT15CMN007)
MOHIT CHIMANKAR
(MT15CMN008)

2. Contents
• Fuzzy Numbers
• Linguistic Variables
• Arithmetic Operations On Fuzzy Intervals
• Arithmetic Operations On Fuzzy Numbers
2

3. 4.1 Fuzzy Numbers
• Set A : R [0,1]
• To qualify as fuzzy number, a fuzzy set A on R must have following
properties:
1. Set A must be Normal Fuzzy set;
2. α-cut of A must be closed interval for every α in (0,1];
3. Support and strong α-cut of A must be bounded.
 Every Fuzzy number is a Convex fuzzy set, The Inverse is not
necessarily true.
3

4. Examples of fuzzy quantities :
Real number Fuzzy number/interval
4
4.1 Fuzzy Numbers

5. 4.2 Linguistic Variables
• It is fully described by name of the variable, linguistic values,
base variable range, various rules.
• A numerical variables takes numerical values: Age = 65
• A linguistic variables takes linguistic values: Age is old
• All such linguistic values set is a fuzzy set.
5

6. Example: Linguistic variable age :
6
4.2 Linguistic Variables

7. • Appearance = {beautiful, pretty, cute, handsome, attractive, not
beautiful, very pretty, very very handsome, more or less pretty,
quite pretty, quite handsome, fairly handsome, not very attractive..}
• Truth = {true, not true, very true, completely true, more or less
true, fairly true, essentially true, false, very false...}
• Age = {young, not young, very young, middle aged, not middle
aged, old, not old, very old, more or less old, not very young and
not very old...}
7
4.2 Linguistic Variables
Example: Linguistic variables :

8. 4.3 Arithmetic Operations On Intervals
• Fuzzy arithmetic is based on two properties :
– Each fuzzy set and thus each fuzzy number is uniquely be
represented by its α-cuts;
– α-cut of A must be closed intervals of real numbers for all
α in (0,1].
Using above properties we define arithmetic operations
on fuzzy numbers in terms of arithmetic operations on
their α cuts.
Later operations are subject to interval analysis
8

9. • [a, b]*[d, e]={f*g|a ≤ f ≤ b, d ≤ g ≤ e}
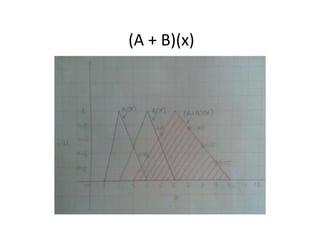
1. Addition
[a, b]+[d, e]=[a+d, b+e];
2. Subtraction
[a, b]-[d, e]=[a-e, b-d];
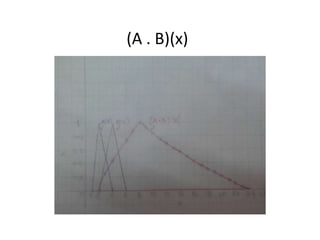
3.Multiplication
[a, b].[d, e]=[min(ad,ae,bd,be), max(ad,ae,bd,be)];
4. Division*
[a, b]/[d, e]=[a, b].[1/e, 1/d]
=[min(a/d,a/e,b/d,b/e), max(a/d,a/e,b/d,b/e)].
5. Inverse Interval*
[d,e] inverse =[min(1/d,1/e),max(1/d,1/e)]
* 0 ∉ [d,e] i.e excluding the case d=0 or e=0. 9
4.3 Arithmetic Operations On Intervals
Let * denotes any of the four arithmetic operations on
closed intervals :

10. 1. [-1,3]+[1, 5] = [-1+1, 3+5] = [0, 8]
2 . [-1,3]-[1, 5] = [-1-5, 3-1] = [-6,2]
3. [-1,3].[1, 5] = [min(-1,-5,3,15),max(-1,-5,3,15)]
=[-5,15]
4. [-1,3]/[1, 5] = [-1, 3].[1/1, 1/5]
= [min(-1/1,-1/5,3/1,3/5),max(-1/1,-1/5,3/1,3/5)]
= [-1/1,3/1] = [-1,3]
5. [-2,7]inverse = [min(1/-2,1/7),max(1/-2,1/7)]
= [-1/2,1/7]
10
4.3 Arithmetic Operations On Intervals
Examples illustrating interval-valued arithmetic operations :

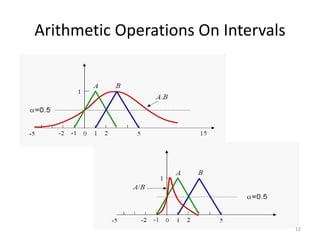
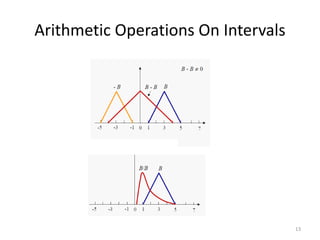
11. Arithmetic Operations On Intervals
A=[-1,3] and B=[1,5]
11

12. Arithmetic Operations On Intervals
12

13. Arithmetic Operations On Intervals
13

14. Properties:
1. Commutativity (+, .) A*B = B*A
2. Associativity (+, .) (A*B)*C = A*(B*C)
3. Identity A = 0+A = A+0 , A = 1.A = A.1
4. Distributivity A.(B+C) = A.B+A.C
5. Subdistributivity A.(B+C)⊆ A.B+A.C
6. Inclusion monotonicity (all). If A ⊆ E & B⊆ F then A*B ⊆ E*F
7. 0, 1 are included in -,/ operations between same fuzzy
intervals respectively. 0 ∈ A-A and 1 ∈ A/A
14
4.3 Arithmetic Operations On Intervals
Arithmetic operations on Fuzzy intervals satisfy following
useful properties :

15. 4.4 Arithmetic Operations On
Fuzzy Numbers
10/28/2016 15
Moving from intervals we can define arithmetic on fuzzy numbers
based on principles of Interval Arithmetic
Let A and B denote fuzzy numbers and let * denote any of the four
basic arithmetic operations. Then, we define a fuzzy set on R, A*B, by
defining its alpha-cut as:

16. 4.4 Arithmetic Operations On Fuzzy Numbers
•

17. (A + B)(x)

18. (A . B)(x)

19. 4.5 Lattice Of Fuzzy Numbers
10/28/2016 19

20. 4.5 Lattice Of Fuzzy Numbers

21. 4.5 Lattice Of Fuzzy Numbers
• How to find MIN?
• Solution
• How to find MAX?
• Solution

22. 4.5 Lattice Of Fuzzy Numbers

23. 4.5 Lattice Of Fuzzy Numbers

24. 10/28/2016 24
4.6 Fuzzy Equations
ABX 

25. 10/28/2016 25

4.6 Fuzzy Equations

26. 10/28/2016 26
1
0.6
α = 0.4
0.8
0.2
0
A B
10 20 30
αa1 = 4
αa2 = 16 αb2 = 26
A(x) , B(x)
x
α b1 – αa1 ≤ α b2 – α a2
αb1 = 14
Fig 5

27. 10/28/2016 27
1
0.6
α = 0.4
β = 0.8
0.2
0
A B
10 20 30
αa1 = 4
αa2 = 16 αb2 = 26
βa1 = 8 βa2 = 12 βb1 = 18 βb2 = 22
αb1 = 14
A(x) , B(x)
x
α b1 – αa1 ≤ β b1 – βa1 ≤ β b2 – βa2 ≤ α b2 – α a2
Fig 6

28. 10/28/2016 28
4.6 Fuzzy Equations

29. 10/28/2016 29
4.6 Fuzzy Equations

30. 10/28/2016 30
4.6 Fuzzy Equations

31. 10/28/2016 31
4.6 Fuzzy Equations

32. THANK YOU.