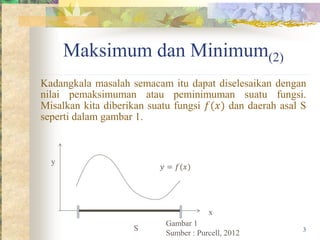
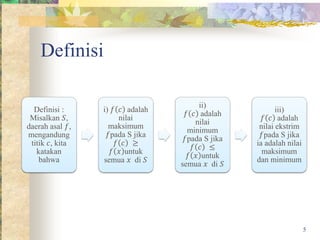
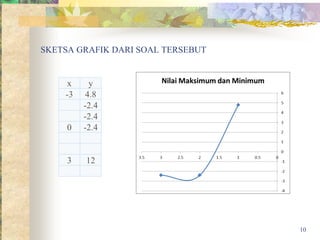
Dokumen ini membahas tentang nilai maksimum dan minimum dalam fungsi serta bagaimana cara mencarinya. Melalui contoh, dijelaskan definisi nilai maksimum, minimum, dan titik stasioner, serta cara menggambar grafik untuk persamaan yang diberikan. Hasil perhitungan menunjukkan nilai maksimum dan minimum pada titik tertentu dalam fungsi kuadrat.

1. NILAI MAKSIMUM DAN MINIMUM
Bahasan Aplikasi dalam Turunan
Monday, April 18, 2016 1

2. Maksimum dan Minimum
Purcell, 2012 menyatakan seringkali kita harus
mencari yang terbaik dalam melakukan sesuatu
pekerjaan.
Contoh :
1. Seorang petani ingin memperoleh kombinasi
tanaman yang dapat menghasilkan keuntungan besar
atau
2. Seorang dokter diharapkan dapat memberikan
dosis terkecil suatu obat untuk menyembuhkan suatu
jenis penyakit.
2

3. Maksimum dan Minimum(2)
Kadangkala masalah semacam itu dapat diselesaikan dengan
nilai pemaksimuman atau peminimuman suatu fungsi.
Misalkan kita diberikan suatu fungsi 𝑓(𝑥) dan daerah asal S
seperti dalam gambar 1.
𝑦 = 𝑓(𝑥)
S
y
x
Gambar 1
Sumber : Purcell, 2012 3

4. PERMASALAHAN
• Kapankah dikatakan apabila 𝑓 𝑥 dikatakan minimum
terhadap S
• Kapankah dikatakan jika fungsi dari x dikatakan memiliki
nilai maksimum
• Dan apabila memiliki nilai ekstrim….
4

5. Definisi :
Misalkan 𝑆,
daerah asal 𝑓,
mengandung
titik 𝑐, kita
katakan
bahwa
i) 𝑓 𝑐 adalah
nilai
maksimum
𝑓pada S jika
𝑓 𝑐 ≥
𝑓 𝑥 untuk
semua 𝑥 di 𝑆
ii)
𝑓 𝑐 adalah
nilai
minimum
𝑓pada S jika
𝑓 𝑐 ≤
𝑓 𝑥 untuk
semua 𝑥 di 𝑆
iii)
𝑓 𝑐 adalah
nilai ekstrim
𝑓pada S jika
ia adalah nilai
maksimum
dan minimum
Definisi
5

6. PENGGAMBARAN TITIK UJUNG, TITIK STASIONER
DAN NILAI MAKSIMUM DAN MINIMUM
• Didalam suatu persamaan fungsi dari x
atau 𝑓 𝑥 =
1
5
6𝑥2
+ 6𝑥 − 12 =
0, dengan I = −3,3 tentukan titik kritis,
titik stasioner dan nilai maksimum dan
minimum serta gambarkan persamaannya.
• Jawaban/Penyelesaian :
Titik ujung dari persamaan ini adalah (-3,3)
6

7. • Titik Stasioner dari persamaan ini diperoleh dari turunan
dari persamaan awal 𝑓 𝑥 .
• 𝑓′ 𝑥 = 𝐷𝑥
1
5
6𝑥2 + 6𝑥 − 12
• =
1
5
12𝑥 + 6 𝑓′ 𝑥 = 0,
•
12𝑥
5
+
6
5
= 0;
•
12𝑥
5
= −
6
5
, 𝑥 = −
6
5
∗
5
12
= −0.5
7

8. PENGGAMBARAN TITIK UJUNG, TITIK STASIONER DAN NILAI
MAKSIMUM DAN MINIMUM(2)
• Nilai Maksimum ketika 𝑓 3 =
1
5
6𝑥2 + 6𝑥 − 12
• =
1
5
6(3)2
+ 6(3) − 12
• = (
1
5
(54 + 18 − 12))
• = (
1
5
*(54+6))
• =
60
5
• = 6
8

9. PENGGAMBARAN TITIK UJUNG, TITIK STASIONER DAN NILAI
MAKSIMUM DAN MINIMUM(3)
• Nilai Minimum ketika 𝑓 −3 =
1
5
6𝑥2 + 6𝑥 − 12
• =
1
5
6(−3)2
+ 6(−3) − 12
• = (
1
5
(54 − 18 − 12))
• = (
1
5
*(54-30))
• =
24
5
• = 4
1
5
9

10. SKETSA GRAFIK DARI SOAL TERSEBUT
x y
-3 4.8
-2.4
-2.4
0 -2.4
3 12
10

11. Monday, April 18, 2016 11