Downloaded 5,403 times
Uploaded byputridkancilofscoutcipecintaakfal
Barisan dan Deret Bilangan ppt
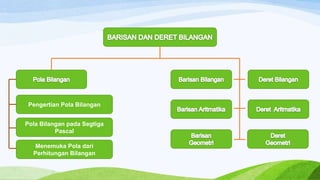
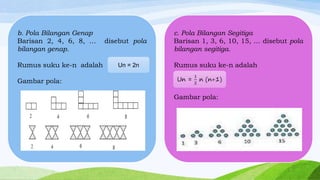
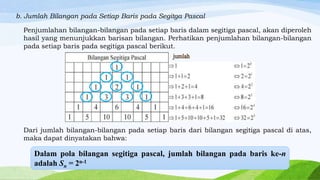
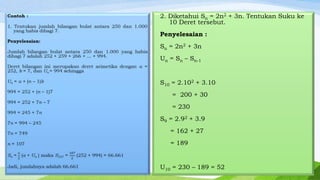
Dokumen tersebut membahas tentang barisan dan deret bilangan. Secara singkat, dibahas tentang (1) pengertian pola bilangan seperti bilangan ganjil, genap, segitiga, persegi, dan persegi panjang, (2) pola bilangan pada segitiga Pascal beserta rumusnya, dan (3) pengertian barisan aritmatika dan deret aritmatika serta rumus untuk menentukan suku ke-n dan jumlah n suku pertama.
More Related Content
![1. BENTUK ALJABAR(s) - Matematika SMP Kelas VIII [www.defantri.com].ppt](https://cdn.slidesharecdn.com/ss_thumbnails/1-240128002039-b16ee847-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Barisan dan Deret Bilangan ppt
Barisan dan Deret Bilangan ppt
- 1. BARISAN DAN DERET BILANGAN PUTRIAFRI FAUZIAH (E1R012041)
- 2. Kelas : IX Semester : II StandarKompetensi : 6. Memahami barisan dan deret bilangan serta penggunaannya dalam pemecahan masalah Kompetensi Dasar : 6.1 Menentukan pola barisan bilangan sederhana 6.2 Menentukan suku ke-n barisan aritmatika dan barisan geometri 6.3 Menentukan jumlah n suku pertama deret aritmatika dan deret geometri 6.4 Memecahkan masalah yang berkaitan dengan barisan dan deret
- 3. Pengertian Pola Bilangan PolaBilangan pada Segtiga Pascal Menemuka Pola dari Perhitungan Bilangan
- 4. A. POLA BILANGAN 1.Pengertian Pola Bilangan Pola bilangan adalah urutan bilangan-bilangan tertentu yang membentuk suatu barisan bilangan. Berikut ini adalah jenis-jenis pola bilangan : a. Pola Bilangan Ganjil Barisan 1, 3, 5, 7, 9, … disebut pola bilangan ganjil. Rumus suku ke-n adalah Gambar pola: Un = 2n-1 ; dengan n bilangan asli
- 5. b. Pola BilanganGenap Barisan 2, 4, 6, 8, … bilangan genap. Rumus suku ke-n adalah disebut pola Un = 2n c. Pola Bilangan Segitiga Barisan 1, 3, 6, 10, 15, … disebut pola bilangan segitiga. Rumus suku ke-n adalah Gambar pola: Gambar pola:
- 6. d. Pola BillanganPersegi Barisan 1, 4, 9, 16, … disebut pola bilangan persegi. e. Pola Bilangan Persegi Panjang Barisan 2, 6, 12, 20, … disebut pola bilangan persegi panjang. Rumus suku ke-n adalah Rumus suku ke-n adalah Un = n2 Un = n (n + 1) Gambar pola : Gambar pola :
- 7. 2. Pola Bilanganpada Segtiga Pascal a. Mengenal Segitiga Pascal Untuk mengetahui bagaimana susunan bilangan-bilangan pada segitiga pascal, maka perlu terlebih dahulu kita memperhatikan papan permainan berikut. Susunan bilangan-bilangan seperti pada gambar disebut segitiga pascal. Kata segitiga diberikan mengingat susunan bilangan-bilangan itu membentuk sebuah segitiga. Sedangkan kata pascal diberikan untuk mengenang Blaise Pascal (1623 - 1662), seorang ahli matematika bangsa Perancis yang menemukan susunan bilanganbilangan tersebut. Jika di perhatikan, ternyata terdapat hubungan antara suatu bilangan dengan jumlah bilangan berdekatan yang terdapat pada baris yang ada tepat di atasnya.
- 8. b. Jumlah Bilanganpada Setiap Baris pada Segitga Pascal Penjumlahan bilangan-bilangan pada setiap baris dalam segitiga pascal, akan diperoleh hasil yang menunjukkan barisan bilangan. Perhatikan penjumlahan bilangan-bilangan pada setiap baris pada segitiga pascal berikut. Dari jumlah bilangan-bilangan pada setiap baris dari bilangan segitiga pascal di atas, maka dapat dinyatakan bahwa: Dalam pola bilangan segitiga pascal, jumlah bilangan pada baris ke-n adalah Sn = 2n-1
- 9. Contoh : Berapakah jumlahbilangan pada segitiga pascal pada baris ke-10. c. Penerapan Bilangan Segitiga Pascal pada Binomial Newton Penyelesaian : Segitiga Pascal dapat digunakan untuk menentukan koefisien pada suku banyak (x+y)n dengan n bilangan asli. n = 10 Misalnya, Sn = 2n–1 • (x + y)1 = 1x + 1y = x + y S10= 210–1 • (x + y)2 = 1x2 + 2xy + 1y2 = x2 + 2xy + y2 = 29 • (x + y)3 = 1x3 + 3x2 y + 3xy = 512 Jadi, jumlah bilangan segitiga pascal pada baris ke-10 adalah 512. 2 + 1y3 = x3 + 3x2 y + 3xy 2+y3 • (x + y)4 = 1x4 + 4x3y + 6x2y2 + 4xy3 + 1y4 = x4 + 4x3y2 + 4xy3 + y4
- 10. 3. Menemuka Poladari Perhitungan Bilangan Pada Bagian 1, telah kita pelajari pola bilangan ganjil. Jumlah bilangan-bilangan ganjil berurutan (jumlah n bilangan ganjil yang pertama) akan memiliki pola tertentu, yaitu : Sekarang, amatilah pola bilangan dari perhitungan berikut ini. 22 – 12 = 4 – 1 = 3 = 2 + 1, 32 – 22 = 9 – 4 = 5 = 3 + 2, 1+ 3 = 4 = 22, 42 – 32 = 16 – 9 = 7 = 4 + 3, 1 + 3 + 5 = 9 = 32 , 52 – 42 = 25 – 16 = 9 = 5 + 4, dan seterusnya. 1+ 3 + 5 + 7 = 16 = 42, dan seterusnya. Pola bilangan tersebut menunjukkan bahwa selisih dari kuadrat bilangan berurutan sama dengan jumlah dari bilangan berurutan tersebut. Hal ini dapat ditunjukkan dengan cara aljabar berikut ini. Jika kita perhatikan, akan diperoleh : a. Jumlah dua bilangan ganjil yang pertama sama dengan kuadrat dari bilangan 2, b. Jumlah tiga bilangan ganjil yang pertama sama dengan kuadrat dari bilangan 3, c. Jumlah empat bilangan ganjil yang pertama sama dengan kuadrat dari bilangan 4, dan seterusnya. Misalkan, bilangan yang berurutan itu adalah a dan a + 1 maka (a + 1)2 – a2 = a2 + 2a + 1 – a2 = 2a + 1 = (a + 1) + a Pola bilangan tersebut selalu benar untuk setiap a bilangan asli.
- 11. B. BARISAN DANDERET BILANGAN 1. Barisan Bilangan Barisan bilangan adalah bilangan-bilangan yang diurutkan dengan pola (aturan) tertentu. Misalnya : a. 40, 44, 48, 52, … b. 1, 3, 5, 7, 9, … c. 2, 4, 6, 8, 10, … Bilangan-bilangan yang membentuk suatu barisan bilangan disebut suku barisan tersebut. Misalnya, pada barisan bilangan ganjil 1, 3, 5, 7, ... suku ke-1 dari barisan tersebut adalah 1, suku ke-2 adalah 3, suku ke-3 adalah 5, dan seterusnya. Jadi, suatu barisan bilangan dapat dikatakan sebagai suatu barisan yang dibentuk oleh sukusuku bilangan. Suatu barisan bilangan dapat pula dibentuk dari bilangan-bilangan yang tidak mempunyai pola (aturan) tertentu, misalnya barisan bilangan 1, 2, 5, 7, 3, 4, ... Barisan bilangan seperti ini disebut barisan bilangan sebarang.
- 12. 2. Deret Bilangan Amatikembali barisan-barisan bilangan berikut. a. 40, 44, 48, 52, … b. 1, 3, 5, 7, … c. 2, 4, 6, 8, … Berdasarkan pola ketiga barisan tersebut, dapat diperoleh penjumlahan berikut. a. 40 + 44 + 48 + 52 + … b. 1 + 3 + 5 + 7 + 9 + … c. 2 + 4 + 6 + 8 + 10 + … Penjumlahan suku-suku dari barisan-barisan tersebut dinamakan deret. Oleh karena itu, jika U1, U2, U3, ..., Un adalah suatu barisan bilangan maka U1 + U2 + U3 + ... + Un dinamakan deret.
- 13. 3. Barisan Aritmatika Amatiketiga barisan bilangan berikut. a. 1, 3, 5, 7, 9, ..., Un, Suatu barisan U1, U2, U3, ..., Un, Un + 1 dinamakan barisan aritmetika jika untuk setiap n bilangan asli memenuhi (Un + 1) – Un = Un – (Un–1) = ... = U2 – U1 = b b. 99, 96, 93, 90, ..., Un, Jika suku pertama barisan aritmetika adalah a dengan beda b maka barisan aritmetika U1, U2, U3, ..., Un menjadi c. 1, 2, 5, 7, 12, ..., Un, a , a + b , a + 2b , ..., a + (n – 1) b Selisih dua suku berurutan pada barisan (a) selalu tetap, yaitu 2. Demikian pula selisih dua suku berurutan pada barisan (b) selalu tetap, yaitu 3. Barisan bilangan yang demikian dinamakan barisan aritmetika. Adapun selisih dua suku berurutan pada barisan (c) tidak tetap. Barisan bilangan (c) bukan merupakan barisan aritmetika. a = U1 Pada barisan aritmetika, selisih dua suku berurutan dinamakan beda dan dilambangkan dengan b. Secara umum, barisan aritmetika didefinisikan sebagai berikut. a + b = U2 a + 2b = U3 a + (n – 1)b = Un Dengan demikian, suku ke-n barisan aritmetika dirumuskan sebagai berikut. Un = a + (n – 1) b Menetukan Un jika Sn diketahui Un = Sn – Sn-1
- 14. 4. Deret Aritmatika Berdasarkan pola pertama barisan aritmetikapada Bagian 3, dapat diperoleh penjumlahan sebagai berikut. 1 + 3 + 5 + 7 + ... + Un. Deret ini dinamakan deret aritmetika naik karena nilai Un semakin besar. 99 + 96 + 93 + 90 + ... + Un. Deret ini dinamakan deret aritmetika turun karena nilai Un semakin kecil. Kita dapat menentukan suku-suku pada deret aritmetika sebagai berikut. Misalkan, jumlah n suku pertama deret tersebut dilambangkan dengan Sn maka
- 15. 2. Diketahui Sn= 2n2 + 3n. Tentukan Suku ke 10 Deret tersebut. Penyelesaian : Sn = 2n2 + 3n Un = Sn – Sn-1 S10 = 2.102 + 3.10 = 200 + 30 = 230 S9 = 2.92 + 3.9 = 162 + 27 = 189 U10 = 230 – 189 = 52
- 17.
- 18. 6. Deret Geometri Sepertiyang telah kamu ketahui, jika U1, U2, U3, ..., Un adalah barisan geometri maka suku-sukunya dapat ditulis a, ar, ar2, ar3, ..., arn-1. Dari barisan geometri tersebut, dapat diperoleh barisan penjumlahan berikut. a + ar + ar2 + ar3 + ... + arn-1 Barisan penjumlahan ini disebut deret geometri. Misalkan, jumlah n suku pertama deret geometri dilambang kan dengan Sn maka berlaku hubungan berikut. Sn = a + ar + ar2 + ... + arn–2+ arn–1 rSn = ar + ar2 + ar3 + ... + arn–1 + arn (1 – r)Sn = a – arn (1 - r) Sn = a(1 – rn) Dengan demikian, jumlah n suku pertama deret geometri adalah sebagai berikut.
- 20.