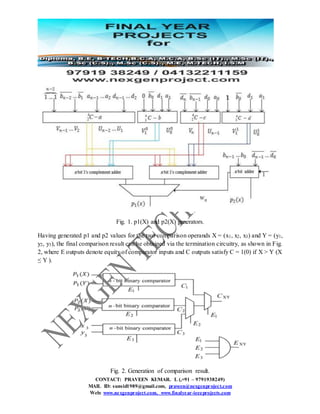
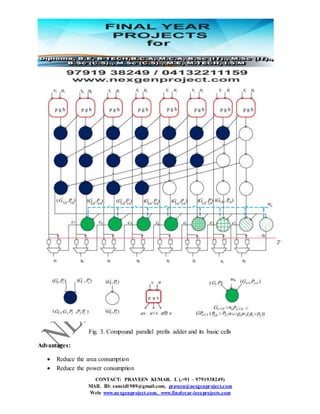
This document discusses the development of a new comparator for residue number systems (RNS) that enhances performance in digital signal processing through reduced power consumption and area efficiency compared to previous methods. It presents an innovative algorithm that partitions the dynamic range and optimizes circuitry using compound parallel prefix architectures. The proposed method demonstrates significant improvements in latency, area usage, and power dissipation, making it suitable for applications requiring efficient arithmetic operations.