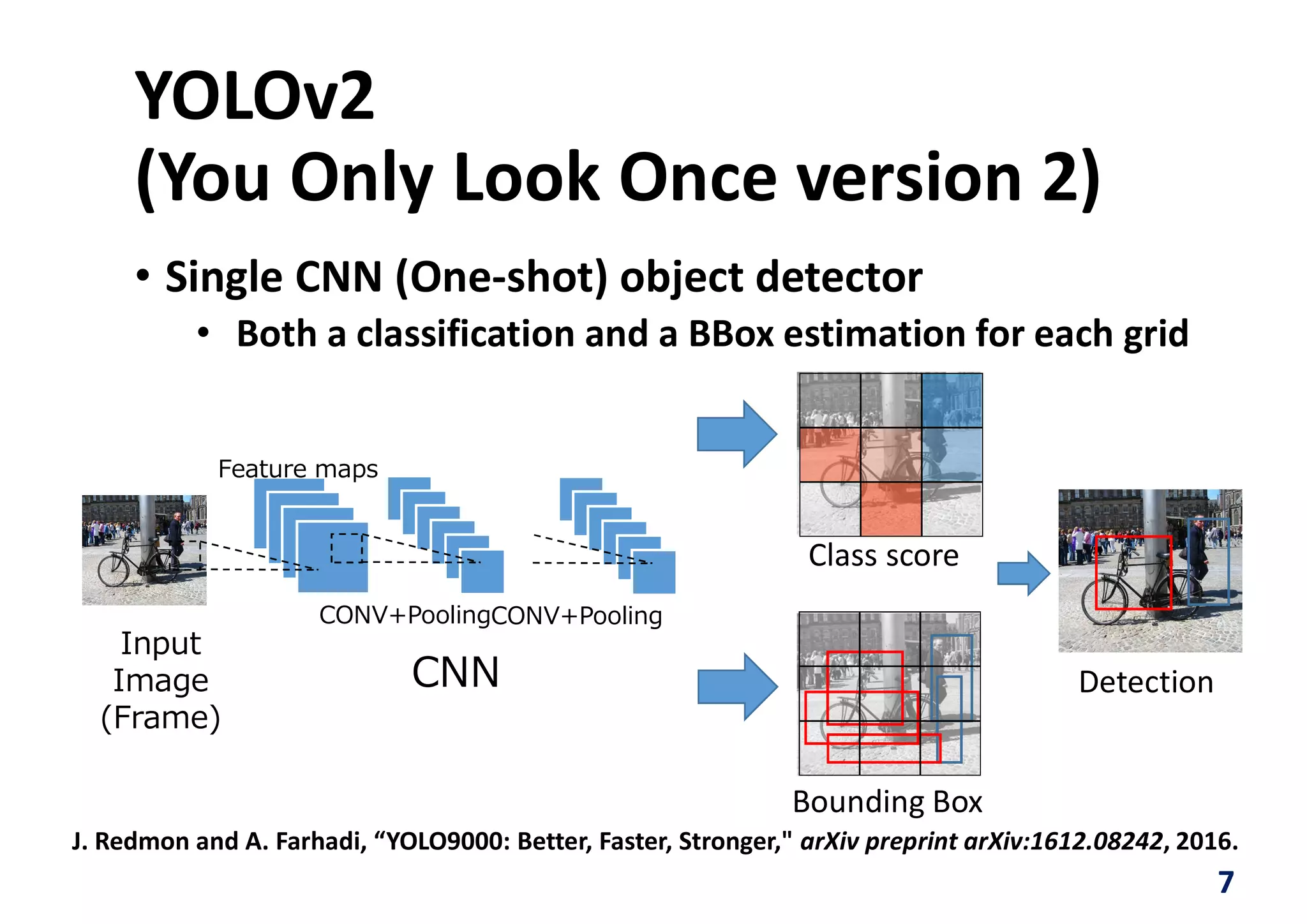
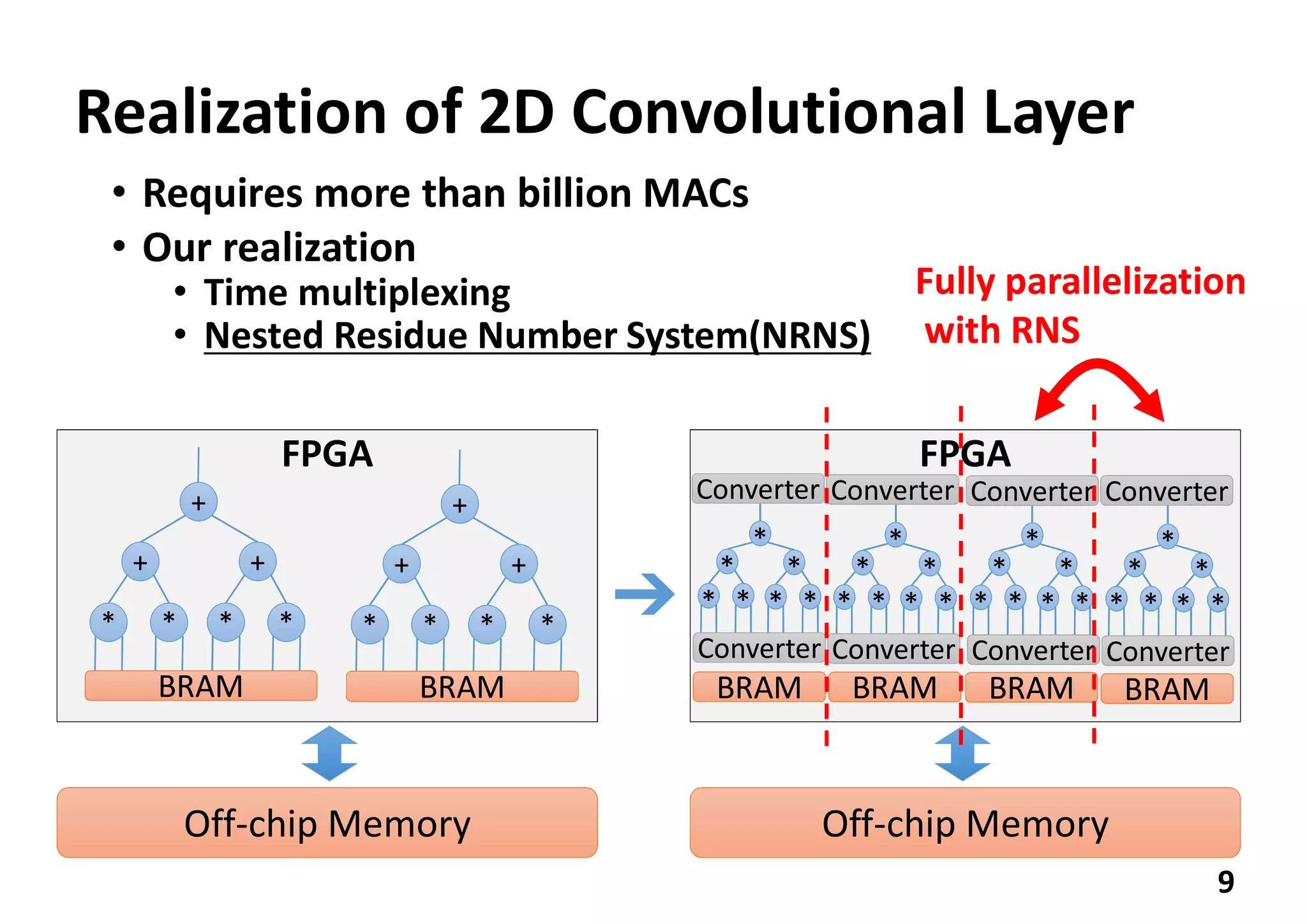
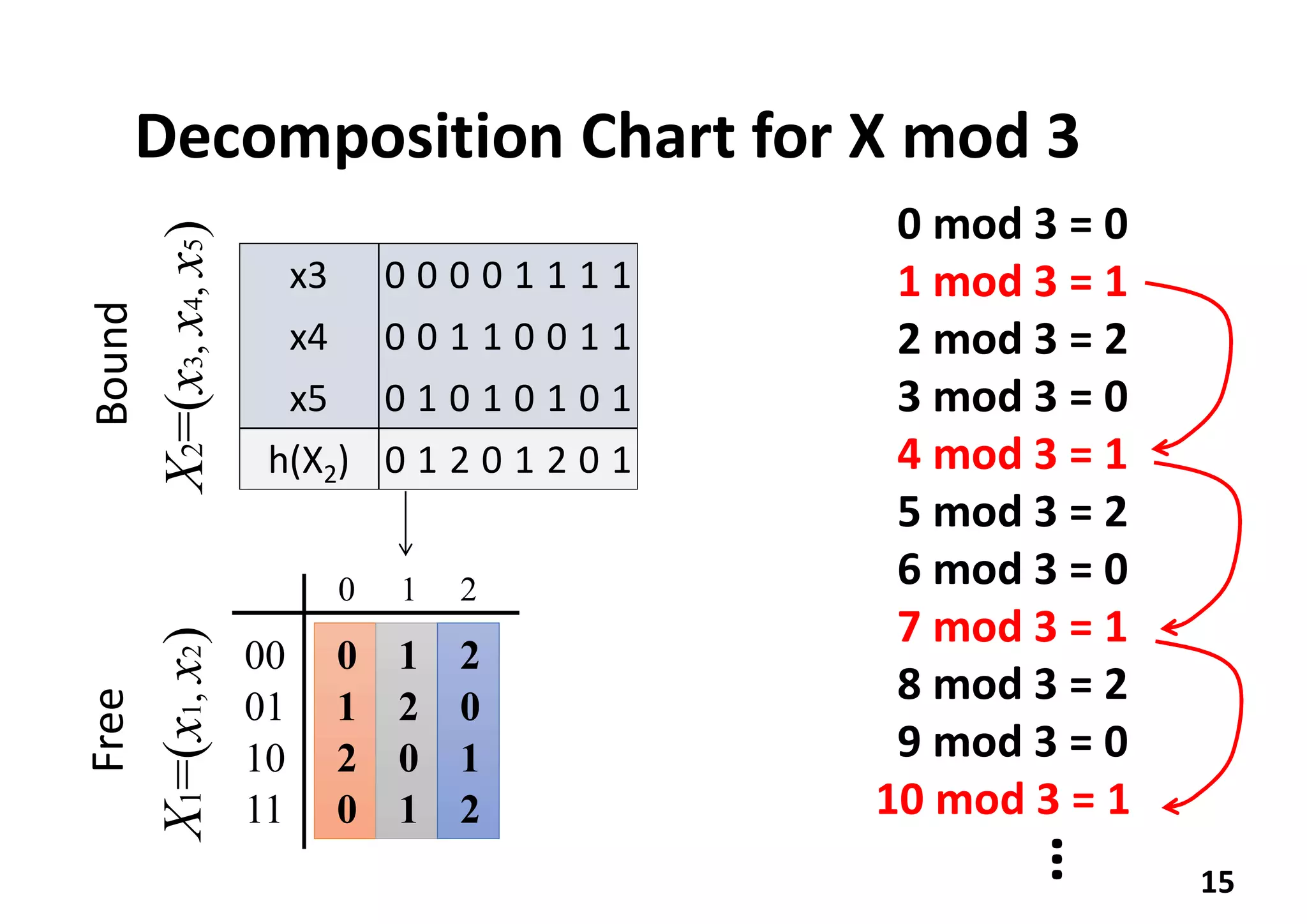
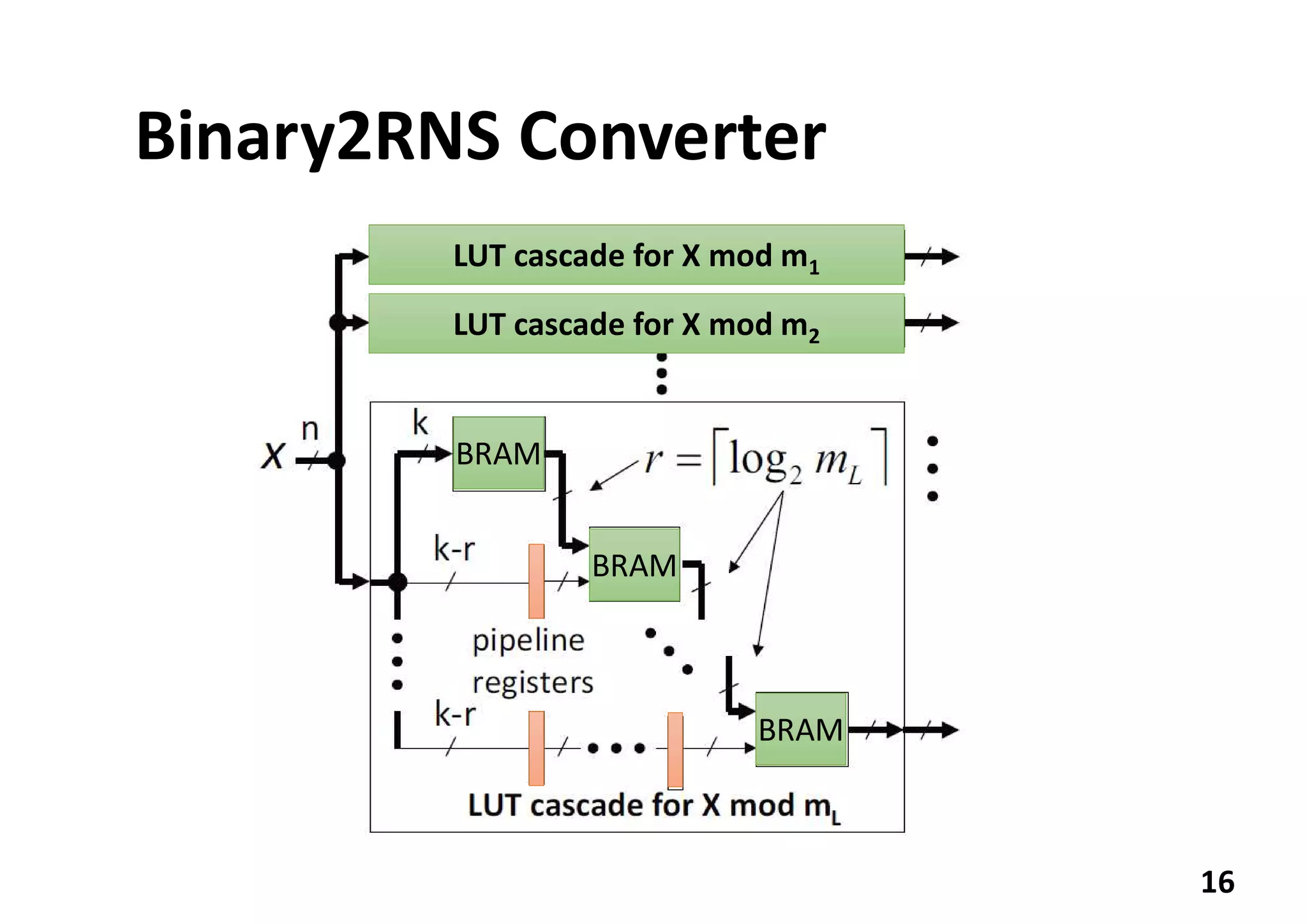
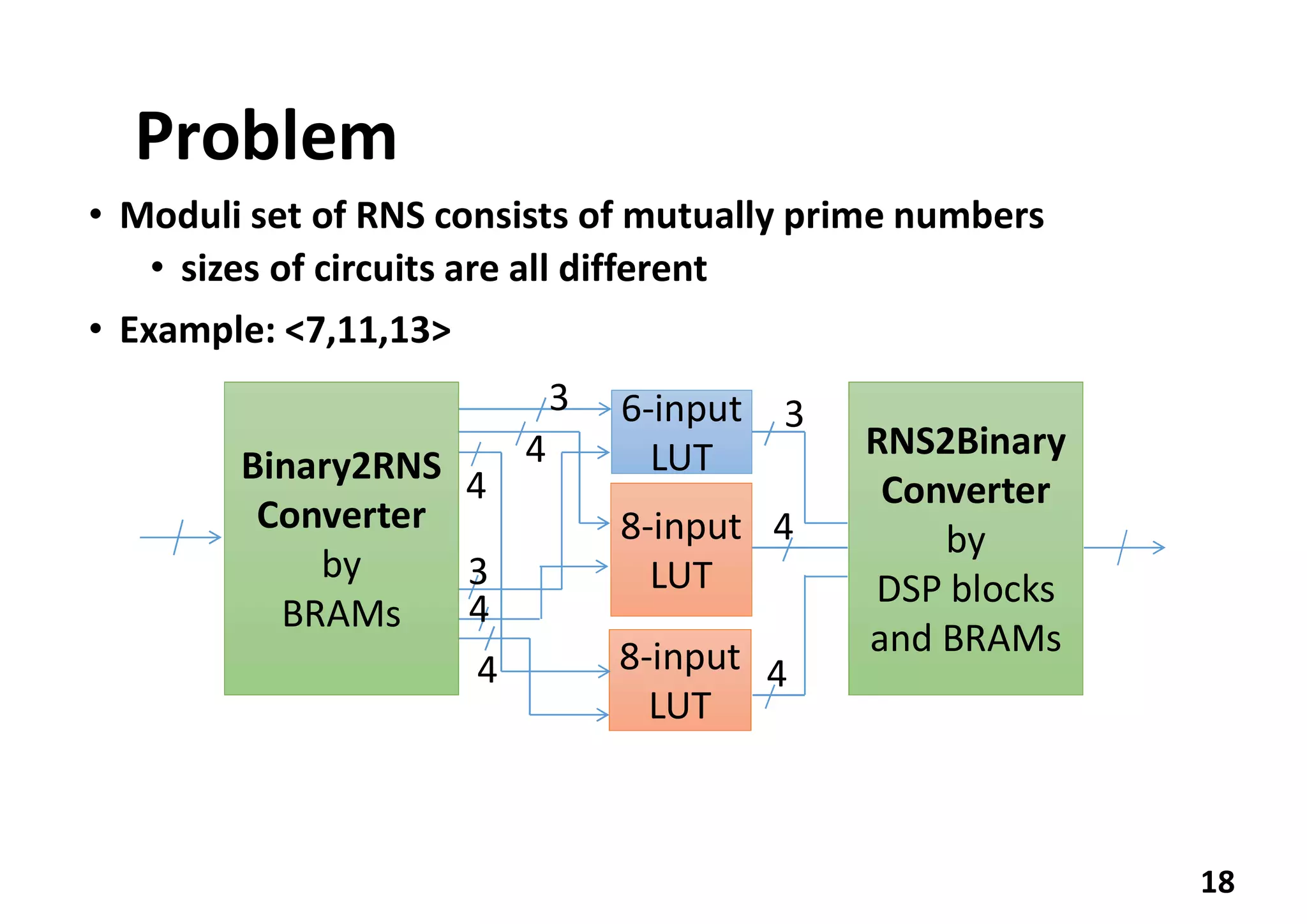
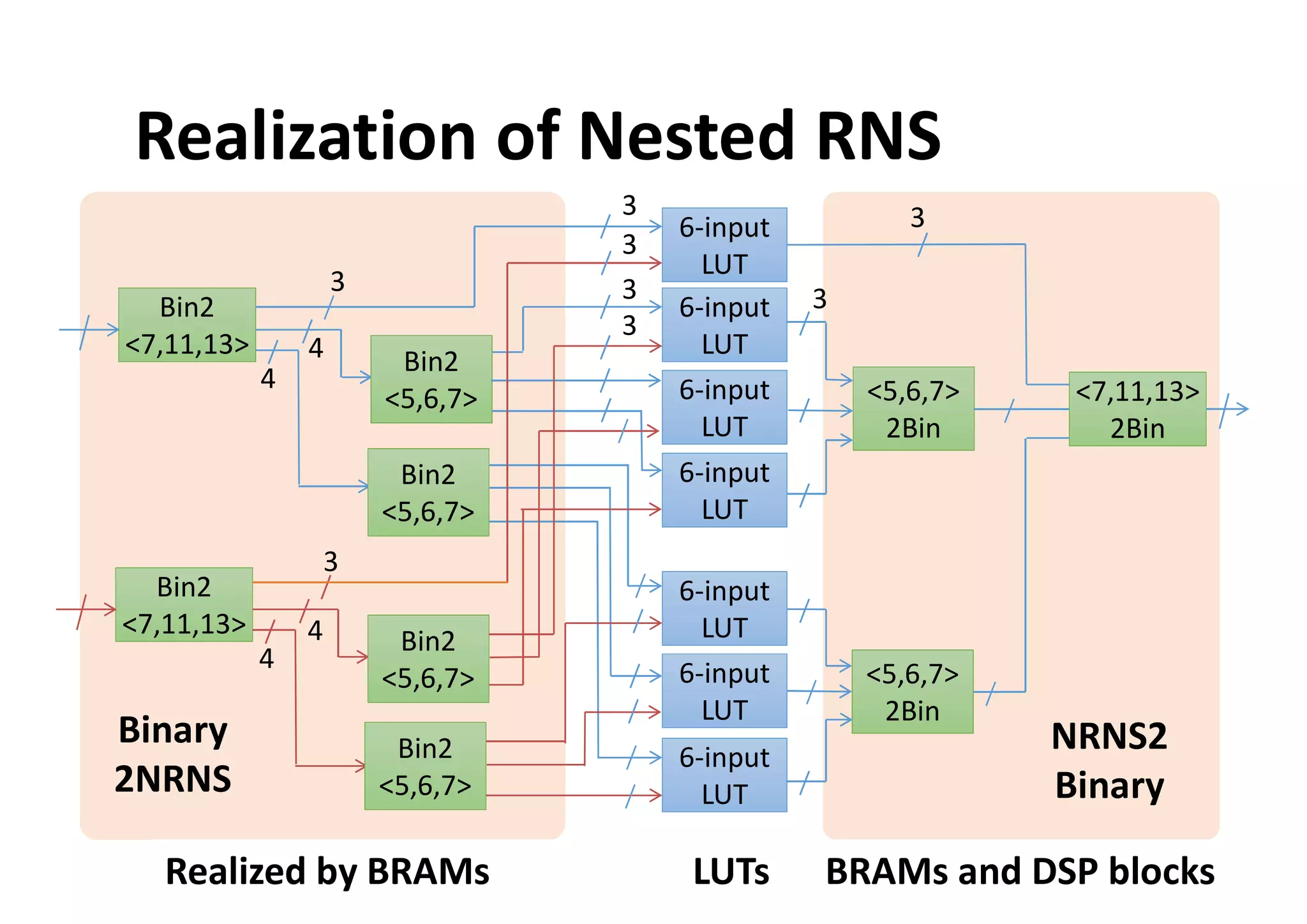
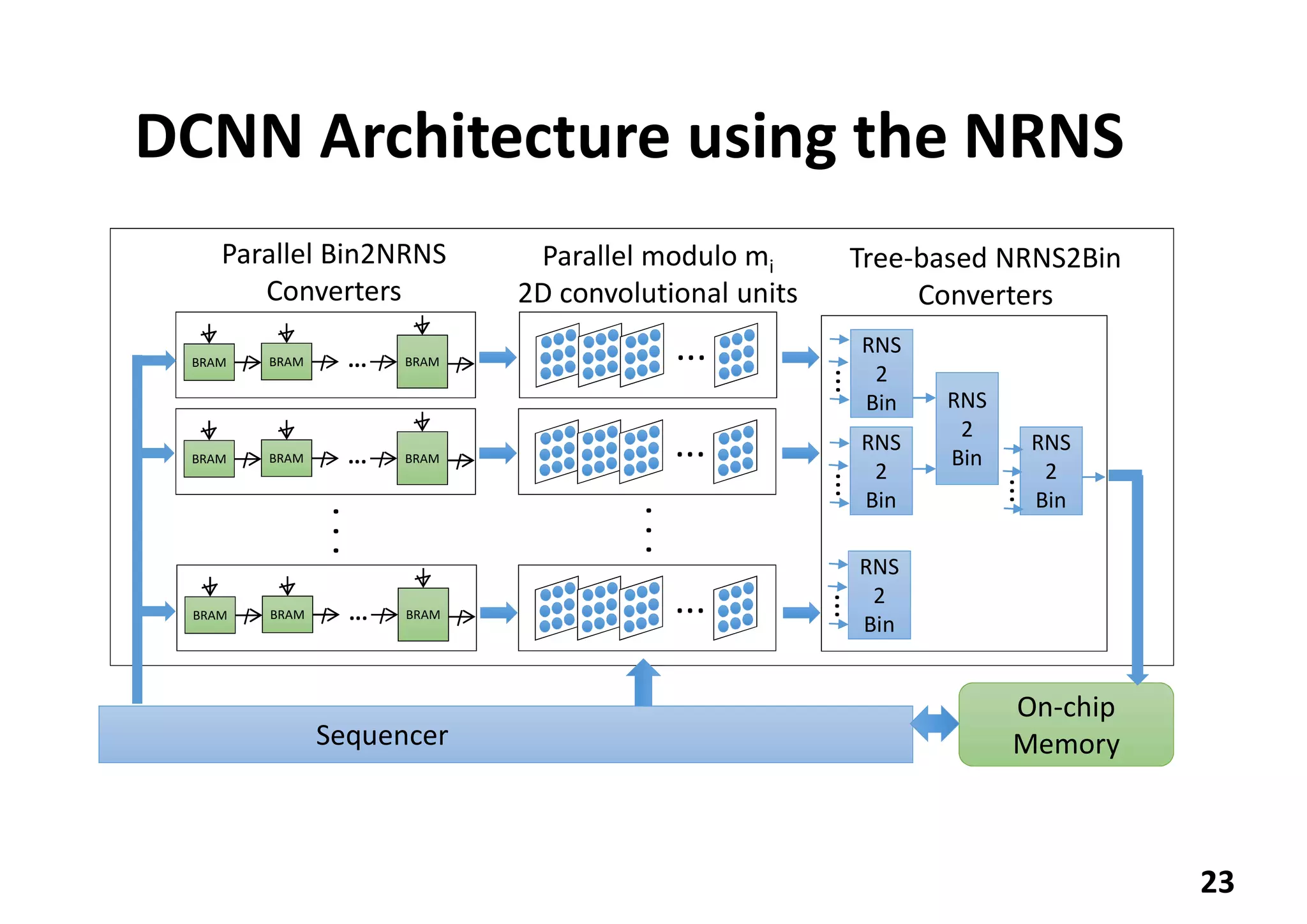
The document discusses implementing a deep neural network object detector called YOLOv2 on an FPGA using a technique called Nested Residue Number System (NRNS). Key points: 1. YOLOv2 is used for real-time object detection but requires high performance and low power. 2. NRNS decomposes large integer operations into smaller ones using a nested set of prime number moduli, enabling parallelization on FPGA. 3. The authors implemented a Tiny YOLOv2 model using NRNS on a NetFPGA-SUME board, achieving 3.84 FPS at 3.5W power and 1.097 FPS/W efficiency.

1. A High-speed Low-power Deep Neural
Network on an FPGA based on the Nested
RNS: Applied to an Object Detector
Hiroki Nakahara, Tokyo Institute of Technology, Japan
Tsutomu Sasao, Meiji University, Japan
ISCAS2018
@Florence

2. Outline
• Background
• YOLOv2
• Convolutional Neural Network (CNN)
• Nested RNS (NRNS) for YOLOv2
• Experimental Results
• Conclusion
2

3. Image Classification by NN
Input Neural Network (NN) Output
3
Cat
(92%)
Improved by AlexNet (Deep Learning)

4. Why?
4
Bigdata
High-Performance
Computing
Algorithm
&Data Structure

5. Object Detection
5
Son
Baby
Daughter
• Detect multiple objects at a time
• High performance-power is necessary

6. Define of Problem
• Detecting and classifying multiple objects at the same time
• Evaluation criteria (from Pascal VOC):
6
Ground truth
annotation
Detection results:
>50% overlap of
bounding box(BBox)
with ground truth
One BBox for each
object
Confidence value
for each object
Person (50%)
, ∈{ ,. ,…, }
Average Precision (AP):

7. YOLOv2
(You Only Look Once version 2)
7
Input
Image
(Frame)
Feature maps
CONV+Pooling
CNN
CONV+Pooling
Class score
Bounding Box
Detection
J. Redmon and A. Farhadi, “YOLO9000: Better, Faster, Stronger," arXiv preprint arXiv:1612.08242, 2016.
• Single CNN (One-shot) object detector
• Both a classification and a BBox estimation for each grid

8. 2D Convolutional Operation
8
Input feature map
Output feature map
Kernel
(Binary)
X0,0 x W0,0
X0,1 x W0,1
X0,2 x W0,2
X1,0 x W1,0
X1,1 x W1,1
X1,2 x W1,2
X2,0 x W2,0
X2,1 x W2,1
+) X2,2 x W2,2
y
• Computational intensive part of the YOLOv2

9. FPGA
Realization of 2D Convolutional Layer
• Requires more than billion MACs
• Our realization
• Time multiplexing
• Nested Residue Number System(NRNS)
9
Off-chip Memory
* *
+
* *
+
+
* *
+
* *
+
+
BRAM BRAM
FPGA
Off-chip Memory
* *
BRAM
*
*
* *
*
* *
BRAM
*
*
* *
*
* *
BRAM
*
*
* *
*
* *
BRAM
*
*
* *
*
➔
Converter Converter Converter Converter
Converter Converter Converter Converter
Fully parallelization
with RNS

10. Residue Number System (RNS)
• Defined by a set of L mutually prime integer constants
〈m1,m2,...,mL〉
• No pair modulus have a common factor with any other
• Typically, prime number is used as moduli set
• An arbitrary integer X can be uniquely represented by
a tuple of L integers (X1,X2,…,XL), where
• Dynamic range:
10
)(mod ii mXX 
M = mi
i=1
L
Õ

11. Parallel Multiplication
Multiplication on RNS
• Moduli set〈3,4,5〉, X=8, Y=2
• Z=X×Y=16=(1,0,1)
• X=(2,0,3), Y=(2,2,2)
Z=(4 mod 3,0 mod 4,6 mod 5)
=(1,0,1)=16
11
Binary2RNS Conversion
RNS2Binary Conversion

12. Binary2RNS Converter
12
X mod 2 mod 3 mod4
0 0 0 0
1 1 1 1
2 0 2 2
3 1 0 3
4 0 1 0
5 1 2 1

13. 13
00 01 10 11
00
01
10
11
0
1
1
1
1
1
0
0
0
1
1
1
1
1
0
0
X1=(x1, x2)
X2=(x3, x4)
h(X1) ０ ０１ １
x1 0 0 1 1
x2 0 1 0 1
h(X1) 0 1 0 1
0 1
00 0 1
01 1 1
10 1 0
11 1 0
x3,x4
h(X1)
Functional Decomposition
24x1=16 [bit] 22x1+23x1=12 [bit]
Column multiplicity=2
Bound variables
Free
variables

14. Decomposition Chart for X mod 3
14
000 001 010 011
00
01
10
11
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
X2=(x3, x4, x5)
X1=(x1,x2)
100 101 110 111
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
0 mod 3 = 0
1 mod 3 = 1
2 mod 3 = 2
3 mod 3 = 0
4 mod 3 = 1
5 mod 3 = 2
6 mod 3 = 0
7 mod 3 = 1
8 mod 3 = 2
9 mod 3 = 0
10 mod 3 = 1
…
Free
variables
Bound variables

15. Decomposition Chart for X mod 3
15
0 1 2
00
01
10
11
0
1
2
0
1
2
0
1
2
0
1
2
X2=(x3,x4,x5)X1=(x1,x2)
FreeBound
x3 0 0 0 0 1 1 1 1
x4 0 0 1 1 0 0 1 1
x5 0 1 0 1 0 1 0 1
h(X2) 0 1 2 0 1 2 0 1
0 mod 3 = 0
1 mod 3 = 1
2 mod 3 = 2
3 mod 3 = 0
4 mod 3 = 1
5 mod 3 = 2
6 mod 3 = 0
7 mod 3 = 1
8 mod 3 = 2
9 mod 3 = 0
10 mod 3 = 1
…

16. Binary2RNS Converter
16
LUT cascade for X mod m1
LUT cascade for X mod m2
BRAM
BRAM
BRAM

17. RNS2Binary Converter (m=30)
17
x1 y1
0 0
1 15
x2 y2
0 0
1 10
2 20
x3 y3
0 0
1 6
2 12
3 18
4 24
Mod m
Adder
Mod m
Adder
carry
carry

18. Problem
• Moduli set of RNS consists of mutually prime numbers
• sizes of circuits are all different
• Example: <7,11,13>
18
6-input
LUT
8-input
LUT
8-input
LUT
3
4
4
4
4
3
3
4
4
Binary2RNS
Converter
by
BRAMs
RNS2Binary
Converter
by
DSP blocks
and BRAMs

19. Nested RNS
• (Z1,Z2,…,Zi,…, ZL) (Z1,Z2,…,(Zi1,Zi2,…,Zij),…, ZL)
• Ex: <7,11,13>×<7,11,13>
<7,<5,6,7>11,<5,6,7>13>×<7,<5,6,7>11,<5,6,7>13>
19
1. Reuse the same moduli set
2. Decompose a large modulo into smaller ones
Original modulus
➔

20. Example of Nested RNS
• 19x22(=418) on <7,<5,6,7>11,<5,6,7>13>
19×22
=<5,8,6>×<1,0,9>
=<5,<3,2,1>11,<1,0,6>13>×<1,<0,0,0>11,<4,3,2>13>
=<5,<0,0,0>11,<4,0,5>13>
=<5,0,2>
=418
20
Modulo Multiplication
Bin2RNS on NRNS
RNS2Bin
Binary2NRNS Conversion

21. Realization of Nested RNS
21
<5,6,7>
2Bin
Bin2
<7,11,13>
3
<7,11,13>
2Bin
<5,6,7>
2Bin
Bin2
<5,6,7>
Bin2
<5,6,7>
6-input
LUT
6-input
LUT
6-input
LUT
6-input
LUT
6-input
LUT
6-input
LUT
6-input
LUT
Bin2
<7,11,13>
Bin2
<5,6,7>
Bin2
<5,6,7>
4
4
3
4
4
3
3
3
3
3
3
Binary
2NRNS
NRNS2
Binary
Realized by BRAMs LUTs BRAMs and DSP blocks

22. Moduli Set for NRNS
• Conventional RNS (uses 9 moduli)
<3,5,7,11,13,16,17,19,23>
• Applied the NRNS to moduli that are greater than 16
<3,4,5,7,11,13,16,
<3,4,5,7,11,13>17,
<3,4,5,7,11,13>19,
<3,4,5,7,11,13,<3,4,5,7,11,13>17>23>
22
All the 30 bit MAC operations are decomposed into 4 bit ones

23. DCNN Architecture using the NRNS
23
...
Parallel modulo mi
2D convolutional units
...
...
...
BRAM BRAM BRAM...
BRAM BRAM BRAM...
BRAM BRAM BRAM...
...
Parallel Bin2NRNS
Converters
Tree-based NRNS2Bin
Converters
Sequencer
On-chip
Memory
RNS
2
Bin
RNS
2
Bin
RNS
2
Bin
RNS
2
Bin
RNS
2
Bin
.........
...

24. NRNS based YOLOv2
• Framework: Chainer 1.24.0
• CNN: Tiny YOLOv2
• Benchmark: KITTI
vision benchmark
• mAP: 69.1 %
24

25. Implementation
• FPGA board: NetFPGA-SUME
• FPGA: Virtex7 VC690T
• LUT: 427,014 / 433,200
• 18Kb BRAM: 1,235 / 2,940
• DSP48E: 0 / 3,600
• Realized the pre-trained
NRNS-based YOLOv2
• 9 bit fixed precision
(dynamic range: 30 bit)
• Synthesis tool: Xilinx Vivado2017.2
• Timing constrain: 300MHz
• 3.84 FPS@3.5W → 1.097 FPS/W
25

26. Comparison
26
NVivia Pascal
GTX1080Ti
NetFPGA-SUME
Speed [FPS] 20.64 3.84
Power [W] 60.0 3.5
Efficiency [FPS/W] 0.344 1.097

27. Conclusion
• Realized the DCNN on the FPGA
• Time multiplexing
• Nested RNS
• MAC operation is realized by small LUTs
• Functional decomposition are used as follows:
• Bin2NRNS converter is realized by BRAMs
• NRNS2Bin converter is realized by DSP blocks
and BRAMs
• Performance per power (FPS/W)
• 3.19 times better than Pascal GPU
27