The presentation discusses the arithmetic/logic unit (ALU) of a computer. It provides an overview of topics related to computer arithmetic including number representation methods, addition and multiplication algorithms, and floating-point representation and arithmetic. The ALU performs arithmetic and logical operations and is a key component in the datapath of a processor. Number representation, such as binary, hexadecimal, and floating-point, affects the ease of performing arithmetic operations in hardware.

1. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 1
Part III
The Arithmetic/Logic Unit

2. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 2
About This Presentation
This presentation is intended to support the use of the textbook
Computer Architecture: From Microprocessors toSupercomputers,
Oxford University Press, 2005, ISBN 0-19-515455-X. It is updated
regularly by the author as part of his teaching of the upper-division
course ECE 154, Introduction to Computer Architecture, at the
University of California, Santa Barbara. Instructors can use these
slides freely in classroom teaching and for other educational
purposes. Any other use is strictly prohibited. © Behrooz Parhami
Edition Released Revised Revised Revised Revised
First July 2003 July 2004 July 2005 Mar. 2006 Jan. 2007
Jan. 2008 Jan. 2009 Jan. 2011 Oct. 2014

3. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 3
III The Arithmetic/Logic Unit
Topics in This Part
Chapter 9 Number Representation
Chapter 10 Adders and Simple ALUs
Chapter 11 Multipliers and Dividers
Chapter 12 Floating-Point Arithmetic
Overview of computer arithmetic and ALU design:
• Review representation methods for signed integers
• Discuss algorithms & hardware for arithmetic ops
• Consider floating-point representation & arithmetic

4. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 4
Preview of Arithmetic Unit in the Data Path
Fig. 13.3 Key elements of the single-cycle MicroMIPS data path.
/
ALU Data
cache
Instr
cache
Next addr
Reg
file
op
jta
fn
inst
imm
rs (rs)
(rt)
Data
addr
Data
in
0
1
ALUSrc
ALUFunc DataWrite
DataRead
SE
RegInSrc
rt
rd
RegDst
RegWrite
32
/
16
Register input
Data
out
Func
ALUOvfl
Ovfl
31
0
1
2
Next PC
Incr PC
(PC)
Br&Jump
ALU
out
PC
0
1
2
Instruction fetch Reg access / decode ALU operation Data access
Register
writeback

5. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 5
Computer Arithmetic as a Topic of Study
Brief overview article –
Encyclopedia of Info Systems,
Academic Press, 2002,
Vol. 3, pp. 317-333
Our textbook’s treatment
of the topic falls between
the extremes (4 chaps.)
Graduate course
ECE 252B – Text:
Computer Arithmetic,
Oxford U Press, 2000
(2nd ed., 2010)

6. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 6
9 Number Representation
Arguably the most important topic in computer arithmetic:
• Affects system compatibility and ease of arithmetic
• Two’s complement, flp, and unconventional methods
Topics in This Chapter
9.1 Positional Number Systems
9.2 Digit Sets and Encodings
9.3 Number-Radix Conversion
9.4 Signed Integers
9.5 Fixed-Point Numbers
9.6 Floating-Point Numbers

7. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 7
9.1 Positional Number Systems
Representations of natural numbers {0, 1, 2, 3, …}
||||| ||||| ||||| ||||| ||||| || sticks or unary code
27 radix-10 or decimal code
11011 radix-2 or binary code
XXVII Roman numerals
Fixed-radix positional representation with k digits
Value of a number: x = (xk–1xk–2 . . . x1x0)r = S xi r i
For example:
27 = (11011)two = (124) + (123) + (022) + (121) + (120)
Number of digits for [0, P]: k = logr (P + 1) = logr P + 1
k–1
i=0

8. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 8
Unsigned Binary Integers
Figure 9.1 Schematic representation of 4-bit code for
integers in [0, 15].
0000
0001
1111
0010
1110
0011
1101
0100
1100
1000
0101
1011
0110
1010
0111
1001
0
1
2
3
4
5
6
7
15
11
14
13
12
8
9
10
Inside: Natural number
Outside: 4-bit encoding
0
1
2
3
15
4
5
6
7
8
9
Turn x notches
counterclockwise
to add x
Turn y notches
clockwise
to subtract y
11
14
13
12
10

9. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 9
Representation Range and Overflow
Figure 9.2 Overflow regions in finite number representation systems.
For unsigned representations covered in this section, max – = 0.
max
Finite set of representable numbers
Overflow region
max
Overflow region
Numbers larger
than max
Numbers smaller
than max
 
 
Example 9.2, Part d
Discuss if overflow will occur when computing 317 – 316 in a number
system with k = 8 digits in radix r = 10.
Solution
The result 86 093 442 is representable in the number system which
has a range [0, 99 999 999]; however, if 317 is computed en route to
the final result, overflow will occur.

10. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 10
9.2 Digit Sets and Encodings
Conventional and unconventional digit sets
 Decimal digits in [0, 9]; 4-bit BCD, 8-bit ASCII
 Hexadecimal, or hex for short: digits 0-9 & a-f
 Conventional ternary digit set in [0, 2]
Conventional digit set for radix r is [0, r – 1]
Symmetric ternary digit set in [–1, 1]
 Conventional binary digit set in [0, 1]
Redundant digit set [0, 2], encoded in 2 bits
( 0 2 1 1 0 )two and ( 1 0 1 0 2 )two represent 22

11. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 11
Carry-Save Numbers
Radix-2 numbers using the digits 0, 1, and 2
Example: (1 0 2 1)two = (123) + (022) + (221) + (120) = 13
Possible encodings
(a) Binary (b) Unary
0 00 0 00
1 01 1 01 (First alternate)
2 10 1 10 (Second alternate)
11 (Unused) 2 11
1 0 2 1 1 0 2 1
MSB 0 0 1 0 = 2 First bit 0 0 1 1 = 3
LSB 1 0 0 1 = 9 Second bit 1 0 1 0 = 10

12. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 12
Figure 9.3 Adding a binary number or another
carry-save number to a carry-save number.
The Notion of Carry-Save Addition
Two
carry-save
inputs
Carry-save
input
Binary input
Carry-save
output
This bit
being 1
represents
overflow
(ignore it)
0
0
0
a. Carry-save addition. b. Adding two carry-save numbers.
Carry-save
addition
Carry-save
addition
Digit-set combination: {0, 1, 2} + {0, 1} = {0, 1, 2, 3} = {0, 2} + {0, 1}

13. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 13
9.3 Number Radix Conversion
 Perform arithmetic in the new radix R
Suitable for conversion from radix r to radix 10
Horner’s rule:
(xk–1xk–2 . . . x1x0)r = (…((0 + xk–1)r + xk–2)r + . . . + x1)r + x0
(1 0 1 1 0 1 0 1)two = 0 + 1  1  2 + 0  2  2 + 1  5  2 + 1 
11  2 + 0  22  2 + 1  45  2 + 0  90  2 + 1  181
 Perform arithmetic in the old radix r
Suitable for conversion from radix 10 to radix R
Divide the number by R, use the remainder as the LSD
and the quotient to repeat the process
19 / 3  rem 1, quo 6 / 3  rem 0, quo 2 / 3  rem 2, quo 0
Thus, 19 = (2 0 1)three
Two ways to convert numbers from an old radix r to a new radix R

14. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 14
Justifications for Radix Conversion Rules
Figure 9.4 Justifying one step of the conversion of x to radix 2.
x
0
x mod 2
Binary representation of x/2
Justifying Horner’s rule.
1 2
1 2 0 1 2 1 0
( ) k k
k k r k k
x x x x r x r x r x
 
   
    
0 1 2
( ( ( )))
x r x r x r
   

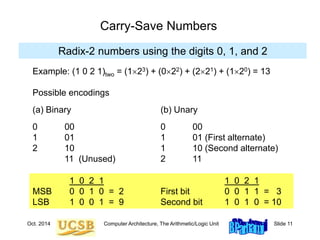
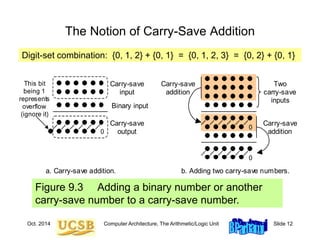
15. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 15
9.4 Signed Integers
 We dealt with representing the natural numbers
 Signed or directed whole numbers = integers
{ . . . , 3, 2, 1, 0, 1, 2, 3, . . . }
 Signed-magnitude representation
+27 in 8-bit signed-magnitude binary code 0 0011011
–27 in 8-bit signed-magnitude binary code 1 0011011
–27 in 2-digit decimal code with BCD digits 1 0010 0111
 Biased representation
Represent the interval of numbers [N, P] by the unsigned
interval [0, P + N]; i.e., by adding N to every number

16. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 16
Two’s-Complement Representation
Figure 9.5 Schematic representation of 4-bit 2’s-complement
code for integers in [–8, +7].
0000
0001
1111
0010
1110
0011
1101
0100
1100
1000
0101
1011
0110
1010
0111
1001
+0
+1
+2
+3
+4
+5
+6
+7
–1
–5
–2
–3
–4
–8
–7
–6
+
_
0
1
2
3
–1
4
5
6
7
–8
–7
Turn x notches
counterclockwise
to add x
Turn 16 – y notches
counterclockwise to
add –y (subtract y)
–5
–2
–3
–4
–6
With k bits, numbers in the range [–2k–1, 2k–1 – 1] represented.
Negation is performed by inverting all bits and adding 1.

17. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 17
Conversion from 2’s-Complement to Decimal
Example 9.7
Convert x = (1 0 1 1 0 1 0 1)2’s-compl to decimal.
Solution
Given that x is negative, one could change its sign and evaluate –x.
Shortcut: Use Horner’s rule, but take the MSB as negative
–1  2 + 0  –2  2 + 1  –3  2 + 1  –5  2 + 0  –10  2 + 1
 –19  2 + 0  –38  2 + 1  –75
Example 9.8
Sign Change for a 2’s-Complement Number
Given y = (1 0 1 1 0 1 0 1)2’s-compl, find the representation of –y.
Solution
–y = (0 1 0 0 1 0 1 0) + 1 = (0 1 0 0 1 0 1 1)2’s-compl (i.e., 75)

18. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 18
Two’s-Complement Addition and Subtraction
Figure 9.6 Binary adder used as 2’s-complement adder/subtractor.
AddSub
x  y
y
x
k
/
k
/
k
/
y or
y 
Adder
cout
cin
k
/

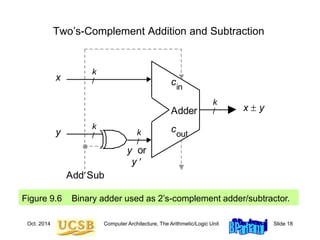
19. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 19
9.5 Fixed-Point Numbers
Positional representation: k whole and l fractional digits
Value of a number: x = (xk–1xk–2 . . .x1x0 .x–1x–2 . . . x–l )r = S xi r i
For example:
2.375 = (10.011)two = (121) + (020) + (021) + (122) + (123)
Numbers in the range [0, rk – ulp] representable, where ulp = r –l
Fixed-point arithmetic same as integer arithmetic
(radix point implied, not explicit)
Two’s complement properties (including sign change) hold here as well:
(01.011)2’s-compl = (–021) + (120) + (02–1) + (12–2) + (12–3) = +1.375
(11.011)2’s-compl = (–121) + (120) + (02–1) + (12–2) + (12–3) = –0.625

20. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 20
Fixed-Point 2’s-Complement Numbers
Figure 9.7 Schematic representation of 4-bit 2’s-complement
encoding for (1 + 3)-bit fixed-point numbers in the range [–1, +7/8].
0.000
0.001
1.111
0.010
1.110
0.011
1.101
0.100
1.100
1.000
0.101
1.011
0.110
1.010
0.111
1.001
+0
+.125
+.25
+.375
+.5
+.625
+.75
+.875
–.125
–.625
–.25
–.375
–.5
–1
–.875
–.75
+
_

21. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 21
Radix Conversion for Fixed-Point Numbers
 Perform arithmetic in the new radix R
Evaluate a polynomial in r –1: (.011)two = 0  2–1 + 1  2–2 + 1  2–3
Simpler: View the fractional part as integer, convert, divide by r l
(.011)two = (?)ten
Multiply by 8 to make the number an integer: (011)two = (3)ten
Thus, (.011)two = (3 / 8)ten = (.375)ten
 Perform arithmetic in the old radix r
Multiply the given fraction by R, use the whole part as the MSD
and the fractional part to repeat the process
(.72)ten = (?)two
0.72  2 = 1.44, so the answer begins with 0.1
0.44  2 = 0.88, so the answer begins with 0.10
Convert the whole and fractional parts separately.
To convert the fractional part from an old radix r to a new radix R:

22. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 22
9.6 Floating-Point Numbers
 Fixed-point representation must sacrifice precision
for small values to represent large values
x = (0000 0000 . 0000 1001)two Small number
y = (1001 0000 . 0000 0000)two Large number
 Neither y2 nor y / x is representable in the format above
 Floating-point representation is like scientific notation:
20 000 000 = 2  107 +0.000 000 007 = +7  10–9
Useful for applications where very large and very small
numbers are needed simultaneously
Also, 7E9
Significand
Exponent
Exponent base
Sign

23. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 23
ANSI/IEEE Standard Floating-Point Format (IEEE 754)
Figure 9.8 The two ANSI/IEEE standard floating-point formats.
Short (32-bit) format
Long (64-bit) format
Sign Exponent Significand
8 bits,
bias = 127,
–126 to 127
11 bits,
bias = 1023,
–1022 to 1023
52 bits for fractional part
(plus hidden 1 in integer part)
23 bits for fractional part
(plus hidden 1 in integer part)
Short exponent range is –127 to 128
but the two extreme values
are reserved for special operands
(similarly for the long format)
Revision (IEEE 754R) was completed in 2008: The revised version includes
16-bit and 128-bit binary formats, as well as 64- and 128-bit decimal formats

24. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 24
Short and Long IEEE 754 Formats: Features
Table 9.1 Some features of ANSI/IEEE standard floating-point formats
Feature Single/Short Double/Long
Word width in bits 32 64
Significand in bits 23 + 1 hidden 52 + 1 hidden
Significand range [1, 2 – 2–23] [1, 2 – 2–52]
Exponent bits 8 11
Exponent bias 127 1023
Zero (±0) e + bias = 0, f = 0 e + bias = 0, f = 0
Denormal e + bias = 0, f ≠ 0
represents ±0.f  2–126
e + bias = 0, f ≠ 0
represents ±0.f  2–1022
Infinity (∞) e + bias = 255, f = 0 e + bias = 2047, f = 0
Not-a-number (NaN) e + bias = 255, f ≠ 0 e + bias = 2047, f ≠ 0
Ordinary number e + bias  [1, 254]
e  [–126, 127]
represents 1.f  2e
e + bias  [1, 2046]
e  [–1022, 1023]
represents 1.f  2e
min 2–126  1.2  10–38 2–1022  2.2  10–308
max  2128  3.4  1038  21024  1.8  10308
Subnormal

25. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 25
10 Adders and Simple ALUs
Addition is the most important arith operation in computers:
• Even the simplest computers must have an adder
• An adder, plus a little extra logic, forms a simple ALU
Topics in This Chapter
10.1 Simple Adders
10.2 Carry Propagation Networks
10.3 Counting and Incrementation
10.4 Design of Fast Adders
10.5 Logic and Shift Operations
10.6 Multifunction ALUs

26. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 26
10.1 Simple Adders
Figures 10.1/10.2 Binary half-adder (HA) and full-adder (FA).
x y c s
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
Inputs Outputs
HA
x y
c
s
x y c c s
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Inputs Outputs
cout cin
out
in x y
s
FA
Digit-set interpretation:
{0, 1} + {0, 1}
= {0, 2} + {0, 1}
Digit-set interpretation:
{0, 1} + {0, 1} + {0, 1}
= {0, 2} + {0, 1}

27. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 27
Full-Adder Implementations
Figure10.3 Full adder implemented with two half-adders, by means
of two 4-input multiplexers, and as two-level gate network.
(a) FA built of two HAs
(c) Two-level AND-OR FA
(b) CMOS mux-based FA
1
0
3
2
HA
HA
1
0
3
2
0
1
x
y
x
y
x
y
s
s
s
cout
cout
cout
cin
cin
cin

28. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 28
Ripple-Carry Adder: Slow But Simple
Figure 10.4 Ripple-carry binary adder with 32-bit inputs and output.
x
s
y
c
c
x
s
y
c
x
s
y
c
cout cin
0 0
0
c0
1 1
1
1
2
31
31
31
31
FA FA FA
32
. . .
Critical path

29. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 29
Carry Chains and Auxiliary Signals
Bit positions
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
----------- ----------- ----------- -----------
1 0 1 1 0 1 1 0 0 1 1 0 1 1 1 0
cout 0 1 0 1 1 0 0 1 1 1 0 0 0 0 1 1 cin
__________/__________________/ ________/____/
4 6 3 2
Carry chains and their lengths
g = xy p = x  y

30. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 30
Carry Chains Illustrated with Dominoes

31. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 31
10.2 Carry Propagation Networks
Figure 10.5 The main part of an adder is the carry network. The rest
is just a set of gates to produce the g and p signals and the sum bits.
Carry network
. . . . . .
xi
yi
g p
s
i
i
i
ci
ci+1
ck1
ck
ck2
c1
c0
g p1
1 g p0
0
g pk2
k2
g pi+1
i+1
g pk1
k1
c0
. . . . . .
0 0
0 1
1 0
1 1
annihilated or killed
propagated
generated
(impossible)
Carry is:
gi
pi
gi = xi yi
pi = xi  yi

32. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 32
Ripple-Carry Adder Revisited
Figure 10.6 The carry propagation network of a ripple-carry adder.
. . .
ck1
ck
ck2 c1
g p1
1 g p0
0
g pk2
k2
g pk1
k1
c0
c2
The carry recurrence: ci+1 = gi  pi ci
Latency of k-bit adder is roughly 2k gate delays:
1 gate delay for production of p and g signals, plus
2(k – 1) gate delays for carry propagation, plus
1 XOR gate delay for generation of the sum bits

33. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 33
The Complete Design of a Ripple-Carry Adder
Figure 10.6 (ripple-carry network) superimposed on
Figure 10.5 (general structure of an adder).
Carry network
. . . . . .
xi
yi
g p
s
i
i
i
ci
ci+1
ck1
ck
ck2
c1
c0
g p1
1 g p0
0
g pk2
k2
g pi+1
i+1
g pk1
k1
c0
. . . . . .
0 0
0 1
1 0
1 1
annihilated or killed
propagated
generated
(impossible)
Carry is:
gi
pi
gi = xi yi
pi = xi  yi
. . .
ck1
ck
ck2 c1
g p1
1 g p0
0
g pk2
k2
g pk1
k1
c0
c2
. . .
ck1
ck
ck2 c1
g p1
1 g p0
0
g pk2
k2
g pk1
k1
c0
c2

34. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 34
First Carry Speed-Up Method: Carry Skip
Figures 10.7/10.8 A 4-bit section of a ripple-carry network
with skip paths and the driving analogy.
c
g p4j+1
4j+1 g p4j
4j
g p4j+2
4j+2
g p4j+3
4j+3
c4j
4j+4 c4j+3 c4j+2 c4j+1
One-way street
Freeway

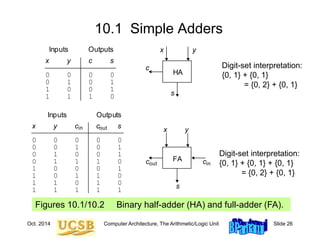
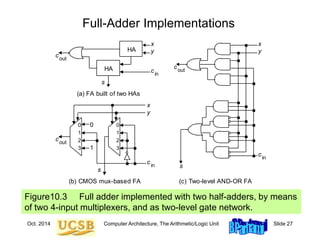
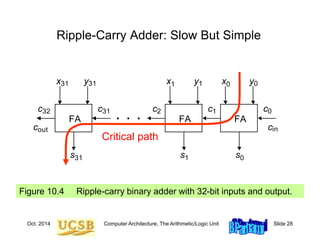
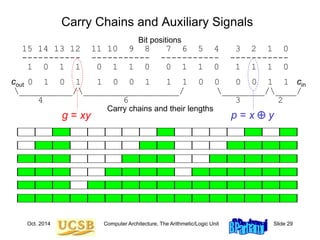
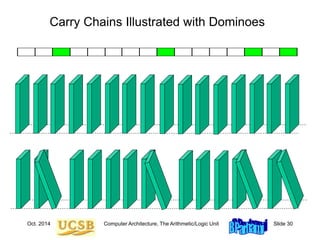
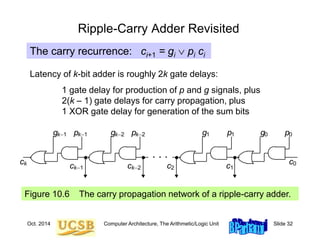
35. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 35
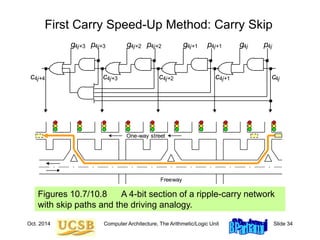
Mux-Based Skip Carry Logic
The carry-skip adder of Fig. 10.7 works fine if we begin with a
clean slate, where all signals are 0s; otherwise, it will run into
problems, which do not exist in this mux-based implementation
c
g p4j+1
4j+1 g p4j
4j
g p4j+2
4j+2
g p4j+3
4j+3
c4j
4j+4 c4j+3 c4j+2 c4j+1
0
1
p[4j, 4j+3]
c4j+4
c
g p4j+1
4j+1 g p4j
4j
g p4j+2
4j+2
g p4j+3
4j+3
c4j
4j+4 c4j+3 c4j+2 c4j+1
Fig. 10.7

36. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 36
10.3 Counting and Incrementation
Figure 10.9 Schematic diagram of an initializable synchronous counter.
D Q
C
_
Q
D
cout
cin
Adder
Update
/
k
k
/
a
(Increment
amount)
Count
register k
/
1
0
Data in
k
/
k
/
IncrInit

37. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 37
Circuit for Incrementation by 1
Substantially
simpler than
an adder
Figure 10.10 Carry propagation network
and sum logic for an incrementer.
1 0
k2
k1
. . .
ck1
ck ck2 c1
x x
x
x
c2
1 0
k2
k1 s s
s
s 2
s
. . .
ck1
ck
ck2 c1
g p1
1 g p0
0
g pk2
k2
g pk1
k1
c0
c2
0
0
x0
x1
Figure 10.6
1

38. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 38
 Carries can be computed directly without propagation
 For example, by unrolling the equation for c3, we get:
c3 = g2  p2 c2 = g2  p2 g1  p2 p1 g0  p2 p1 p0 c0
 We define “generate” and “propagate” signals for a block
extending from bit position a to bit position b as follows:
g[a,b] = gb  pb gb–1  pb pb–1gb–2  . . .  pb pb–1…pa+1 ga
p[a,b] = pb pb–1. . . pa+1 pa
 Combining g and p signals for adjacent blocks:
g[h,j] = g[i+1,j]  p[i+1,j] g[h,i]
p[h,j] = p[i+1,j] p[h,i]
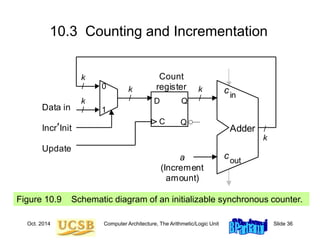
10.4 Design of Fast Adders
h
i
i+1
j
[h, j] = [i + 1, j] ¢ [h, i]

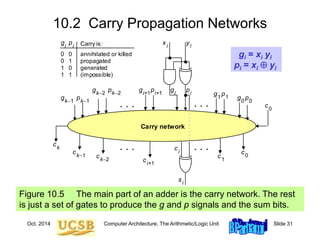
39. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 39
Carries as Generate Signals for Blocks [ 0, i]
Figure 10.5
Carry network
. . . . . .
xi
yi
g p
s
i
i
i
ci
ci+1
ck1
ck
ck2
c1
c0
g p1
1 g p0
0
g pk2
k2
g pi+1
i+1
g pk1
k1
c0
. . . . . .
0 0
0 1
1 0
1 1
annihilated or killed
propagated
generated
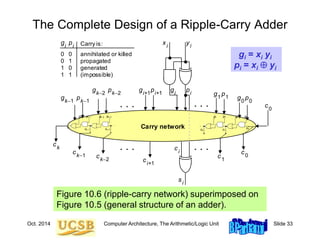
(impossible)
Carry is:
gi
pi
Assuming c0 = 0,
we have ci = g[0,i –1]

40. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 40
Second Carry Speed-Up Method: Carry Lookahead
Figure 10.11 Brent-Kung lookahead carry network for an 8-digit adder,
along with details of one of the carry operator blocks.
¢ ¢ ¢ ¢
¢ ¢
¢ ¢
¢ ¢ ¢
[7, 7] [6, 6] [5, 5] [4, 4] [3, 3] [2, 2] [1, 1] [0, 0]
[0, 7] [0, 6] [0, 5] [0, 4] [0, 3] [0, 2] [0, 1] [0, 0]
[2, 3]
[4, 5]
[6, 7]
[4, 7]
[0, 3]
[0, 1]
g[0, 0]
g[0, 1]
g[1, 1]
p[0, 0]
p[0, 1]
p[1, 1]

41. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 41
Recursive Structure of Brent-Kung Carry Network
Figure 10.12 Brent-Kung lookahead carry network for an 8-digit adder,
with only its top and bottom rows of carry-operators shown.
¢ ¢ ¢ ¢
¢ ¢ ¢
[7, 7] [6, 6] [5, 5] [4, 4] [3, 3] [2, 2] [1, 1] [0, 0]
[0, 7] [0, 6] [0, 5] [0, 4] [0, 3] [0, 2] [0, 1] [0, 0]
4-input Brent-Kung
carry network
¢ ¢ ¢ ¢
¢ ¢
¢ ¢
¢ ¢ ¢
[7, 7] [6, 6] [5, 5] [4, 4] [3, 3] [2, 2] [1, 1] [0, 0]
[0, 7] [0, 6] [0, 5] [0, 4] [0, 3] [0, 2] [0, 1] [0, 0]
[2, 3]
[4, 5]
[6, 7]
[4, 7]
[0, 3]
[0, 1]

42. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 42
An Alternate Design: Kogge-Stone Network
Kogge-Stone lookahead carry network for an 8-digit adder.
¢ ¢ ¢ ¢
¢ ¢ ¢ ¢
¢ ¢
¢ ¢
¢ ¢
¢
¢ ¢
c1 = g[0,0]
c2 = g[0,1]
c3 = g[0,2]
c8 = g[0,7] c4 = g[0,3]
c5 = g[0,4]
c6 = g[0,5]
c7 = g[0,6]

43. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 43
¢ ¢ ¢ ¢
¢ ¢
¢ ¢
¢ ¢ ¢
[7, 7] [6, 6] [5, 5] [4, 4] [3, 3] [2, 2] [1, 1] [0, 0]
[0, 7] [0, 6] [0, 5] [0, 4] [0, 3] [0, 2] [0, 1] [0, 0]
[2, 3]
[4, 5]
[6, 7]
[4, 7]
[0, 3]
[0, 1]
g[0, 0]
g[0, 1]
g[1, 1]
p[0, 0]
p[0, 1]
p[1, 1]
Brent-Kung vs. Kogge-Stone Carry Network
11 carry operators
4 levels
17 carry operators
3 levels

44. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 44
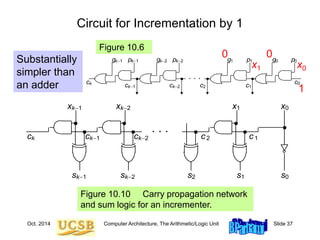
Carry-Lookahead Logic with 4-Bit Block
Figure 10.13 Blocks needed in the design of carry-lookahead adders
with four-way grouping of bits.
Block
signal
generation
p[i, i+3]
ci
Intermeidte
carries
ci+1
ci+2
ci+3
g[i, i+3]
pi+3
gi+3
pi+2
gi+2
pi+1
gi+1
pi
gi

45. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 45
Third Carry Speed-Up Method: Carry Select
Figure 10.14 Carry-select addition principle.
cout
cin
Adder
Version 1
of sum bits
1
0
x
[a, b]
cout
cin
Adder
Version 0
of sum bits
y
[a, b]
s
[a, b]
c
a
0 1
Allows doubling of adder width with a single-mux additional delay
The lower
a positions,
(0 to a – 1)
are added
as usual

46. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 46
10.5 Logic and Shift Operations
Conceptually, shifts can be implemented by multiplexing
Figure 10.15 Multiplexer-based logical shifting unit.
Multiplexer
0 1 2 31 32 33 62 63
5
6
Right’Left
Shift amount 0, x[31, 1]
x[31, 0]
00, x[30, 2]
00...0, x[31]
x[31, 0]
x[30, 0], 0
x[1, 0], 00...0
x[0], 00...0
. . . . . .
32
32 32
32
32
32
32
32
32
6-bit code specifying
shift direction & amount
Right-shifted
values
Left-shifted
values

47. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 47
Arithmetic Shifts
Figure 10.16 The two arithmetic shift instructions of MiniMIPS.
Purpose: Multiplication and division by powers of 2
sra $t0,$s1,2 # $t0  ($s1) right-shifted by 2
srav $t0,$s1,$s0 # $t0  ($s1) right-shifted by ($s0)
1
1
1 1
0 0 0
fn
0 0 0 0 0 0 0 0 0 0 0 1 0
0
0 0 1 1
1
0 0 0 0 0
0 0 0
31 25 20 15 0
ALU
instruction
Unused Source
register
op rs rt
R
rd sh
10 5
Destination
register
Shift
amount
sra = 3
1
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0
0 0 1 1
1
1 0 0 0 0 0
0 0 0
31 25 20 15 0
ALU
instruction
Amount
register
Source
register
op rs rt
R
rd sh
10 5
fn
Destination
register
Unused srav = 7

48. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 48
Practical Shifting in Multiple Stages
Figure 10.17 Multistage shifting in a barrel shifter.
2
0, x[31, 1]
x[31, 0]
x[30, 0], 0
32
0 1 2 3
32 32 32 32
0 0 No shift
0 1 Logical left
1 0 Logical right
1 1 Arith right
x[31], x[31, 1]
Multiplexer
2
0 1 2 3
(0 or 4)-bit shift
2
0 1 2 3
(0 or 2)-bit shift
2
0 1 2 3
(0 or 1)-bit shift
(a) Single-bit shifter (b) Shifting by up to 7 bits
y[31, 0]
z[31, 0]

49. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 49
Figure 10.18 A 4  8 block of a black-and-white
image represented as a 32-bit word.
Bit Manipulation via Shifts and Logical Operations
AND with mask to isolate a field: 0000 0000 0000 0000 1111 1100 0000 0000
Right-shift by 10 positions to move field to the right end of word
The result word ranges from 0 to 63, depending on the field pattern
32-pixel (4  8) block of
black-and-white image:
1010 0000 0101 1000 0000 0110 0001 0111
Representation
as 32-bit word:
Hex equivalent: 0xa0a80617
Row 0 Row 1 Row 2 Row 3
Bits 10-15

50. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 50
10.6 Multifunction ALUs
General structure of a simple arithmetic/logic unit.
Logic
unit
Arith
unit 0
1
Operand 1
Operand 2
Result
Logic fn (AND, OR, . . .)
Arith fn (add, sub, . . .)
Select fn type
(logic or arith)

51. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 51
An ALU for
MiniMIPS
Figure 10.19 A multifunction ALU with 8 control signals (2 for
function class, 1 arithmetic, 3 shift, 2 logic) specifying the operation.
AddSub
x  y
y
x
Adder
c32
c0
k
/
Shifter
Logic
unit
s
Logic function
Amount
5
2
Constant
amount
Variable
amount
5
5
ConstVar
0
1
0
1
2
3
Function
class
2
Shift function
5 LSBs Shifted y
32
32
32
2
c31
32-
input
NOR
Ovfl
Zero
32
32
MSB
ALU
y
x
s
Shorthand
symbol
for ALU
Ovfl
Zero
Func
Control
0 or 1
AND 00
OR 01
XOR 10
NOR 11
00 Shift
01 Set less
10 Arithmetic
11 Logic
00 No shift
01 Logical left
10 Logical right
11 Arith right

52. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 52
11 Multipliers and Dividers
Modern processors perform many multiplications & divisions:
• Encryption, image compression, graphic rendering
• Hardware vs programmed shift-add/sub algorithms
Topics in This Chapter
11.1 Shift-Add Multiplication
11.2 Hardware Multipliers
11.3 Programmed Multiplication
11.4 Shift-Subtract Division
11.5 Hardware Dividers
11.6 Programmed Division

53. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 53
11.1 Shift-Add Multiplication
Figure 11.1 Multiplication of 4-bit numbers in dot notation.
Multiplicand
Partial
products
bit-matrix
x
y
z
y x 20
0
y x 21
1
y x 22
2
y x 23
3
Multiplier
Product
z(j+1) = (z(j) + yj x 2k) 2–1 with z(0) = 0 and z(k) = z
|––– add –––|
|–– shift right ––|

54. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 54
Binary and Decimal Multiplication
Figure 11.2 Step-by-step multiplication examples for 4-digit unsigned numbers.
Position 7 6 5 4 3 2 1 0 Position 7 6 5 4 3 2 1 0
========================= =========================
x24 1 0 1 0 x104 3 5 2 8
y 0 0 1 1 y 4 0 6 7
========================= =========================
z(0) 0 0 0 0 z(0) 0 0 0 0
+y0x24 1 0 1 0 +y0x104 2 4 6 9 6
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(1) 0 1 0 1 0 10z(1) 2 4 6 9 6
z(1) 0 1 0 1 0 z(1) 0 2 4 6 9 6
+y1x24 1 0 1 0 +y1x104 2 1 1 6 8
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(2) 0 1 1 1 1 0 10z(2) 2 3 6 3 7 6
z(2) 0 1 1 1 1 0 z(2) 2 3 6 3 7 6
+y2x24 0 0 0 0 +y2x104 0 0 0 0 0
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(3) 0 0 1 1 1 1 0 10z(3) 0 2 3 6 3 7 6
z(3) 0 0 1 1 1 1 0 z(3) 0 2 3 6 3 7 6
+y3x24 0 0 0 0 +y3x104 1 4 1 1 2
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(4) 0 0 0 1 1 1 1 0 10z(4) 1 4 3 4 8 3 7 6
z(4) 0 0 0 1 1 1 1 0 z(4) 1 4 3 4 8 3 7 6
========================= =========================
Example 11.1

55. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 55
Two’s-Complement Multiplication
Figure 11.3 Step-by-step multiplication examples for 2’s-complement numbers.
Position 7 6 5 4 3 2 1 0 Position 7 6 5 4 3 2 1 0
========================= =========================
x24 1 0 1 0 x24 1 0 1 0
y 0 0 1 1 y 1 0 1 1
========================= =========================
z(0) 0 0 0 0 0 z(0) 0 0 0 0 0
+y0x24 1 1 0 1 0 +y0x24 1 1 0 1 0
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(1) 1 1 0 1 0 2z(1) 1 1 0 1 0
z(1) 1 1 1 0 1 0 z(1) 1 1 1 0 1 0
+y1x24 1 1 0 1 0 +y1x24 1 1 0 1 0
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(2) 1 0 1 1 1 0 2z(2) 1 0 1 1 1 0
z(2) 1 1 0 1 1 1 0 z(2) 1 1 0 1 1 1 0
+y2x24 0 0 0 0 0 +y2x24 0 0 0 0 0
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(3) 1 1 0 1 1 1 0 2z(3) 1 1 0 1 1 1 0
z(3) 1 1 1 0 1 1 1 0 z(3) 1 1 1 0 1 1 1 0
+(–y3x24) 0 0 0 0 0 +(–y3x24) 0 0 1 1 0
–––––––––––––––––––––––––– ––––––––––––––––––––––––––
2z(4) 1 1 1 0 1 1 1 0 2z(4) 0 0 0 1 1 1 1 0
z(4) 1 1 1 0 1 1 1 0 z(4) 0 0 0 1 1 1 1 0
========================= =========================
Example 11.2

56. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 56
11.2 Hardware Multipliers
Multiplier y
Mux
Adder
out
c
0 1
Doublewidth partial product z
Multiplicand x
Shift
Shift
(j)
j
y
Add’Sub
Enable
Select
in
c
Figure 11.4 Hardware multiplier based on the shift-add algorithm.
Hi Lo

57. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 57
The Shift Part of Shift-Add
Figure11.5 Shifting incorporated in the connections to
the partial product register rather than as a separate phase.
out
c
To adder j
y
From adder
Sum
Partial product Multiplier
/ k – 1
/ k – 1
/ k
/ k

58. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 58
High-Radix Multipliers
Radix-4 multiplication in dot notation.
Multiplicand x
y
z
Multiplier
Product
0, x, 2x, or 3x
z(j+1) = (z(j) + yj x 2k) 4–1 with z(0) = 0 and z(k/2) = z
|––– add –––|
|–– shift right ––| Assume k even

59. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 59
Tree Multipliers
Figure 11.6 Schematic diagram for full/partial-tree multipliers.
Adder
Large tree of
carry-save
adders
. . .
All partial products
Product
Adder
Small tree of
carry-save
adders
. . .
Several partial products
Product
Log-
depth
Log-
depth
(a) Full-tree multiplier (b) Partial-tree multiplier

60. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 60
Array Multipliers
Figure 11.7 Array multiplier for 4-bit unsigned operands.
3
2
1
0
4
5
6
7
0
1
2
3
2 1 0
x x x
y
y
y
z
y
3
x 0
0
0
0
0
0
0
0
0
0
0
z
z
z
z
z
z
z
HA
FA
FA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
FA
0
Our original
dot-notation
representing
multiplication
Straightened
dots to depict
array multiplier
to the left
s c
Two
carry-save
inputs
Carry-save
input
Binary input
Carry-save
output
bit
g 1
ents
ow
e it)
0
0
0
a. Carry-save addition. b. Adding two carry-save numbers.
Carry-save
addition
Carry-save
addition
Figure 9.3a
(Recalling
carry-save
addition)

61. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 61
11.3 Programmed Multiplication
MiniMIPS instructions related to multiplication
mult $s0,$s1 # set Hi,Lo to ($s0)($s1); signed
multu $s2,$s3 # set Hi,Lo to ($s2)($s3); unsigned
mfhi $t0 # set $t0 to (Hi)
mflo $t1 # set $t1 to (Lo)
Finding the 32-bit product of 32-bit integers in MiniMIPS
Multiply; result will be obtained in Hi,Lo
For unsigned multiplication:
Hi should be all-0s and Lo holds the 32-bit result
For signed multiplication:
Hi should be all-0s or all-1s, depending on the sign bit of Lo
Example 11.3

62. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 62
Figure 11.8 Register usage for programmed multiplication
superimposed on the block diagram for a hardware multiplier.
Emulating a Hardware Multiplier in Software
$t2 (counter)
Part of the
control in
hardware
Also, holds
LSB of Hi
during shift
Multiplier y
Mux
Adder
out
c
0 1
Doublewidth partial product z
Multiplicand x
Shift
Shift
(j)
j
y
Add’Sub
Enable
Select
in
c
$a0 (multiplicand x)
$a1 (multiplier y)
$v1 (Lo part of z)
$v0 (Hi part of z)
$t0 (carry-out)
$t1 (bit j of y)
Example 11.4 (MiniMIPS shift-add program for multiplication)

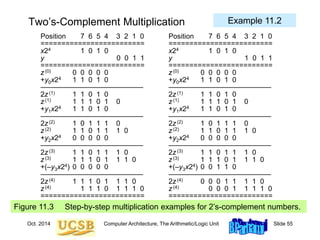
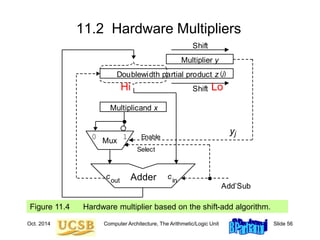
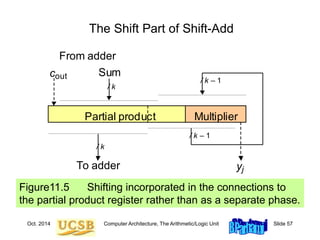
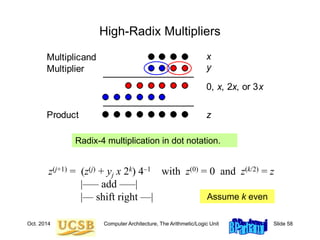
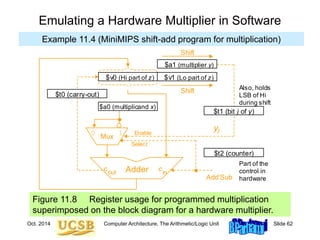
63. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 63
shamu: move $v0,$zero # initialize Hi to 0
move $vl,$zero # initialize Lo to 0
addi $t2,$zero,32 # init repetition counter to 32
mloop: move $t0,$zero # set c-out to 0 in case of no add
move $t1,$a1 # copy ($a1) into $t1
srl $a1,1 # halve the unsigned value in $a1
subu $t1,$t1,$a1 # subtract ($a1) from ($t1) twice to
subu $t1,$t1,$a1 # obtain LSB of ($a1), or y[j], in $t1
beqz $t1,noadd # no addition needed if y[j] = 0
addu $v0,$v0,$a0 # add x to upper part of z
sltu $t0,$v0,$a0 # form carry-out of addition in $t0
noadd: move $t1,$v0 # copy ($v0) into $t1
srl $v0,1 # halve the unsigned value in $v0
subu $t1,$t1,$v0 # subtract ($v0) from ($t1) twice to
subu $t1,$t1,$v0 # obtain LSB of Hi in $t1
sll $t0,$t0,31 # carry-out converted to 1 in MSB of $t0
addu $v0,$v0,$t0 # right-shifted $v0 corrected
srl $v1,1 # halve the unsigned value in $v1
sll $t1,$t1,31 # LSB of Hi converted to 1 in MSB of $t1
addu $v1,$v1,$t1 # right-shifted $v1 corrected
addi $t2,$t2,-1 # decrement repetition counter by 1
bne $t2,$zero,mloop # if counter > 0, repeat multiply loop
jr $ra # return to the calling program
Multiplication When There Is No Multiply Instruction
Example 11.4 (MiniMIPS shift-add program for multiplication)

64. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 64
11.4 Shift-Subtract Division
Figure11.9 Division of an 8-bit number by a 4-bit number in dot notation.
z(j) = 2z(j1)  ykj x 2k with z(0) = z and z(k) = 2k s
|shift|
|–– subtract ––|
2
1
2
y
2
x2
2
1
0
3
0
Subtracted
bit-matrix
Divisor
x
Dividend
z
s Remainder
Quotient
y
y x 3
y x 2
y x

65. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 65
Integer and Fractional Unsigned Division
Figure 11.10 Division examples for binary integers and decimal fractions.
Position 7 6 5 4 3 2 1 0 Position –1 –2 –3 –4 –5 –6 –7 –8
========================= ==========================
z 0 1 1 1 0 1 0 1 z . 1 4 3 5 1 5 0 2
x24 1 0 1 0 x . 4 0 6 7
========================= ==========================
z(0) 0 1 1 1 0 1 0 1 z(0) . 1 4 3 5 1 5 0 2
2z(0) 0 1 1 1 0 1 0 1 10z(0) 1 . 4 3 5 1 5 0 2
–y3x24 1 0 1 0 y3=1 –y–1x 1 . 2 2 0 1 y–1=3
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(1) 0 1 0 0 1 0 1 z(1) . 2 1 5 0 5 0 2
2z(1) 0 1 0 0 1 0 1 10z(1) 2 . 1 5 0 5 0 2
–y2x24 0 0 0 0 y2=0 –y–2x 2 . 0 3 3 5 y–2=5
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(2) 1 0 0 1 0 1 z(2) . 1 1 7 0 0 2
2z(2) 1 0 0 1 0 1 10z(2) 1 . 1 7 0 0 2
–y1x24 1 0 1 0 y1=1 –y–3x 0 . 8 1 3 4 y–3=2
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(3) 1 0 0 0 1 z(3) . 3 5 6 6 2
2z(3) 1 0 0 0 1 10z(3) 3 . 5 6 6 2
–y0x24 1 0 1 0 y0=1 –y–4x 3 . 2 5 3 6 y–4=8
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(4) 0 1 1 1 z(4) . 3 1 2 6
s 0 1 1 1 s . 0 0 0 0 3 1 2 6
y 1 0 1 1 y . 3 5 2 8
========================= ==========================
Example 11.5

66. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 66
Division with Same-Width Operands
Figure 11.11 Division examples for 4/4-digit binary integers and fractions.
Position 7 6 5 4 3 2 1 0 Position –1 –2 –3 –4 –5 –6 –7 –8
========================= ==========================
z 0 0 0 0 1 1 0 1 z . 0 1 0 1
x24 0 1 0 1 x . 1 1 0 1
========================= ==========================
z(0) 0 0 0 0 1 1 0 1 z(0) . 0 1 0 1
2z(0) 0 0 0 1 1 0 1 2z(0) 0 . 1 0 1 0
–y3x24 0 0 0 0 y3=0 –y–1x 0 . 0 0 0 0 y–1=0
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(1) 0 0 0 1 1 0 1 z(1) . 1 0 1 0
2z(1) 0 0 1 1 0 1 2z(1) 1 . 0 1 0 0
–y2x24 0 0 0 0 y2=0 –y–2x 0 . 1 1 0 1 y–2=1
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(2) 0 0 1 1 0 1 z(2) . 0 1 1 1
2z(2) 0 1 1 0 1 2z(2) 0 . 1 1 1 0
–y1x24 0 1 0 1 y1=1 –y–3x 0 . 1 1 0 1 y–3=1
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(3) 0 0 0 1 1 z(3) . 0 0 0 1
2z(3) 0 0 1 1 2z(3) 0 . 0 0 1 0
–y0x24 1 0 1 0 y0=0 –y–4x 0 . 0 0 0 0 y–4=0
–––––––––––––––––––––––––– –––––––––––––––––––––––––––
z(4) 0 0 1 1 z(4) . 0 0 1 0
s 0 0 1 1 s . 0 0 0 0 0 0 1 0
y 0 0 1 0 y . 0 1 1 0
========================= ==========================
Example 11.6

67. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 67
Signed Division
Method 1 (indirect): strip operand signs, divide, set result signs
Dividend Divisor Quotient Remainder
z = 5 x = 3  y = 1 s = 2
z = 5 x = –3  y = –1 s = 2
z = –5 x = 3  y = –1 s = –2
z = –5 x = –3  y = 1 s = –2
Method 2 (direct 2’s complement): develop quotient with digits
–1 and 1, chosen based on signs, convert to digits 0 and 1
Restoring division: perform trial subtraction, choose 0 for q digit
if partial remainder negative
Nonrestoring division: if sign of partial remainder is correct,
then subtract (choose 1 for q digit) else add (choose –1)

68. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 68
11.5 Hardware Dividers
Figure 11.12 Hardware divider based on the shift-subtract algorithm.
Load
Quotient y
Mux
Adder
0 1
Partial remainder z (initially z)
Divisor x
Shift
Shift
(j)
k– j
y
1
Enable
Select
Quotient
digit
selector
1
out
c
in
c
Trial difference
(Always
subtract)
Hi Lo

69. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 69
The Shift Part of Shift-Subtract
Figure 11.13 Shifting incorporated in the connections to the
partial remainder register rather than as a separate phase.
To adder
From adder
Partial remainder Quotient
/ k
/ k
/ k
/ k
k–j
q
MSB

70. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 70
High-Radix Dividers
Radix-4 division in dot notation.
Divisor
x
Dividend
z
s Remainder
Quotient
y
0, x, 2x, or 3x
z(j) = 4z(j1)  (yk2j+1 yk2j)two x 2k with z(0) = z and z(k/2) = 2ks
|shift|
|––––––– subtract –––––––| Assume k even

71. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 71
Array Dividers
Figure 11.14 Array divider for 8/4-bit unsigned integers.
2 1 0
x x x
1
y
2
y
3
y
3
z
0
y
3
x
2
z
1
z
0
z
4
z
5
z
6
z
7
z
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
Our original
dot-notation
for division
Straightened
dots to depict
an array divider
2 1 0
s s s
3
s
0
0
0
0
b d

72. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 72
11.6 Programmed Division
MiniMIPS instructions related to division
div $s0,$s1 # Lo = quotient, Hi = remainder
divu $s2,$s3 # unsigned version of division
mfhi $t0 # set $t0 to (Hi)
mflo $t1 # set $t1 to (Lo)
Compute z mod x, where z (singed) and x > 0 are integers
Divide; remainder will be obtained in Hi
if remainder is negative,
then add |x| to (Hi) to obtain z mod x
else Hi holds z mod x
Example 11.7

73. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 73
Figure 11.15 Register usage for programmed division superimposed
on the block diagram for a hardware divider.
Emulating a Hardware Divider in Software
Example 11.8 (MiniMIPS shift-add program for division)
Load
Quotient y
Mux
Adder
0 1
Partial remainder z (initially z)
Divisor x
Shift
Shift
(j)
k– j
y
1
Enable
Select
Quotient
digit
selector
1
out
c in
c
Trial difference
(Always
subtract)
$t2 (counter)
$a0 (divisor x)
$a1 (quotient y)
$v1 (Lo part of z)
$v0 (Hi part of z)
$t1 (bit kj of y)
Part of the
control in
hardware
$t0 (MSB of Hi)

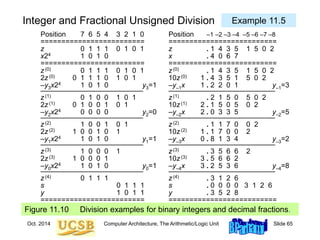
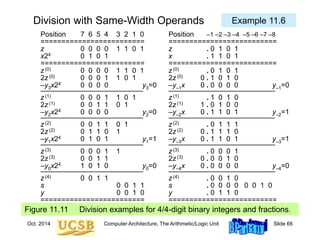
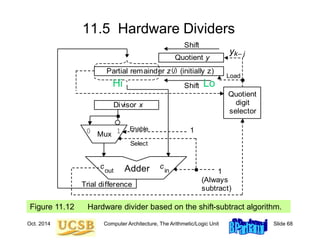
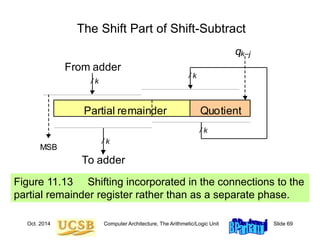
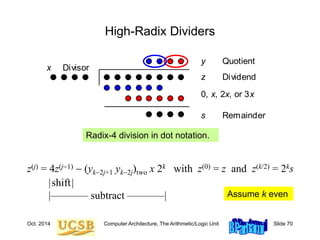
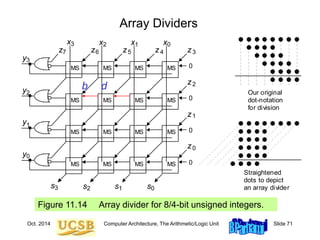
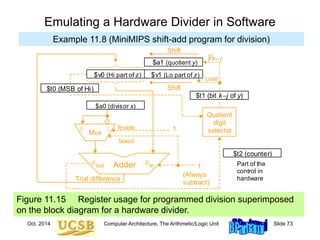
74. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 74
shsdi: move $v0,$a2 # initialize Hi to ($a2)
move $vl,$a3 # initialize Lo to ($a3)
addi $t2,$zero,32 # initialize repetition counter to 32
dloop: slt $t0,$v0,$zero # copy MSB of Hi into $t0
sll $v0,$v0,1 # left-shift the Hi part of z
slt $t1,$v1,$zero # copy MSB of Lo into $t1
or $v0,$v0,$t1 # move MSB of Lo into LSB of Hi
sll $v1,$v1,1 # left-shift the Lo part of z
sge $t1,$v0,$a0 # quotient digit is 1 if (Hi)  x,
or $t1,$t1,$t0 # or if MSB of Hi was 1 before shifting
sll $a1,$a1,1 # shift y to make room for new digit
or $a1,$a1,$t1 # copy y[k-j] into LSB of $a1
beq $t1,$zero,nosub # if y[k-j] = 0, do not subtract
subu $v0,$v0,$a0 # subtract divisor x from Hi part of z
nosub: addi $t2,$t2,-1 # decrement repetition counter by 1
bne $t2,$zero,dloop # if counter > 0, repeat divide loop
move $v1,$a1 # copy the quotient y into $v1
jr $ra # return to the calling program
Division When There Is No Divide Instruction
Example 11.7 (MiniMIPS shift-subtract program for division)

75. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 75
Load
Quotient y
Mux
Adder
0 1
Partial remainder z (initially z)
Divisor x
Shift
Shift
(j)
k– j
y
1
Enable
Select
Quotient
digit
selector
1
out
c
in
c
Trial difference
(Always
subtract)
Multiplier y
Mux
Adder
out
c
0 1
Doublewidth partial product z
Multiplicand x
Shift
Shift
(j)
j
y
Add’Sub
Enable
Select
in
c
Divider vs Multiplier: Hardware Similarities
2 1 0
x x x
1
y
2
y
3
y
3
z
0
y
3
x
2
z
1
z
0
z
4
z
5
z
6
z
7
z
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
MS
Our original
dot-notation
for division
Straightened
dots to depict
an array divider
2 1 0
s s s
3
s
0
0
0
0
Figure 11.12 Figure 11.4
3
2
1
0
4
5
6
7
0
1
2
3
2 1 0
x x x
y
y
y
z
y
3
x 0
0
0
0
0
0
0
0
0
0
0
z
z
z
z
z
z
z
HA
FA
FA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
MA
FA
0
Our original
dot-notation
representing
multiplication
Straightened
dots to depict
array multiplier
to the left
Figure 11.14 Figure 11.7
Turn upside-down

76. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 76
12 Floating-Point Arithmetic
Floating-point is no longer reserved for high-end machines
• Multimedia and signal processing require flp arithmetic
• Details of standard flp format and arithmetic operations
Topics in This Chapter
12.1 Rounding Modes
12.2 Special Values and Exceptions
12.3 Floating-Point Addition
12.4 Other Floating-Point Operations
12.5 Floating-Point Instructions
12.6 Result Precision and Errors

77. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 77
12.1 Rounding Modes
Figure 12.1 Distribution of floating-point numbers on the real line.
Denser Denser
Sparser Sparser
Negative numbers
FLP FLP
0 +
–
Overflow
region
Overflow
region
Underflow
regions
Positive numbers
Underflow
example
Overflow
example
Midway
example
Typical
example
min
max min max
+ +
– –
– +
Denormals allow
graceful underflow
Short (32-bit) format
Long (64-bit) format
Sign Exponent Significand
8 bits,
bias = 127,
–126 to 127
11 bits,
bias = 1023,
–1022 to 1023
52 bits for fractional part
(plus hidden 1 in integer part)
23 bits for fractional part
(plus hidden 1 in integer part)
IEEE 754
Format
0, , NaN
1.f  2e
Denormals:
0.f  2emin

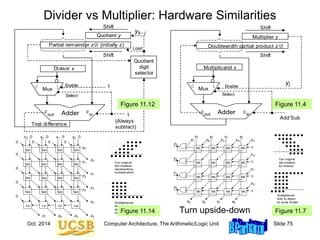
78. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 78
Figure 12.2 Two round-to-nearest-integer functions for x in [–4, 4].
Round-to-Nearest (Even)
rtnei(x)
–4
–3
–2
–1
x
–4 –3 –2 –1 4
3
2
1
4
3
2
1
rtni(x)
–4
–3
–2
–1
x
–4 –3 –2 –1 4
3
2
1
4
3
2
1
(a) Round to nearest even integer (b) Round to nearest integer

79. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 79
Figure 12.3 Two directed round-to-nearest-integer functions for x in [–4, 4].
Directed Rounding
(a) Round inward to nearest integer (b) Round upward to nearest integer
rutni(x)
–4
–3
–2
–1
x
–4 –3 –2 –1 4
3
2
1
4
3
2
1
ritni(x)
–4
–3
–2
–1
x
–4 –3 –2 –1 4
3
2
1
4
3
2
1

80. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 80
12.2 Special Values and Exceptions
Zeros, infinities, and NaNs (not a number)
 0 Biased exponent = 0, significand = 0 (no hidden 1)
  Biased exponent = 255 (short) or 2047 (long), significand = 0
NaN Biased exponent = 255 (short) or 2047 (long), significand  0
Arithmetic operations with special operands
(+0) + (+0) = (+0) – (–0) = +0
(+0)  (+5) = +0
(+0) / (–5) = –0
(+) + (+) = +
x – (+) = –
(+)  x = , depending on the sign of x
x / (+) = 0, depending on the sign of x
(+) = +

81. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 81
Exceptions
Undefined results lead to NaN (not a number)
(0) / (0) = NaN
(+) + (–) = NaN
(0)  () = NaN
() / () = NaN
Arithmetic operations and comparisons with NaNs
NaN + x = NaN NaN < 2  false
NaN + NaN = NaN NaN = Nan  false
NaN  0 = NaN NaN  (+)  true
NaN  NaN = NaN NaN  NaN  true
Examples of invalid-operation exceptions
Addition: (+) + (–)
Multiplication: 0  
Division: 0 / 0 or  / 
Square-root: Operand < 0

82. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 82
12.3 Floating-Point Addition
Figure 12.4 Alignment shift and rounding in floating-point addition.
Operands after alignment shift:
x = 2 1.00101101
y = 2 0.000111101101
Numbers to be added:
x = 2 1.00101101
y = 2 1.11101101
5 

5


Extra bits to be
rounded off
Operand with
smaller exponent
to be preshifted
Result of addition:
s = 2 1.010010111101
s = 2 1.01001100 Rounded sum


5
1
5
5
(2e1s1)
(2e2s2)
+ (2e1(s2 / 2e1–e2)) = 2e1(s1  s2 / 2e1–e2)

83. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 83
Hardware for
Floating-Point
Addition
Figure 12.5
Simplified schematic of
a floating-point adder.
Normalize
& round
Add
Align
significands
Possible swap
& complement
Unpack
Control
& sign
logic
Pack
Input 1
Output
Significands
Exponents
Signs
Significand
Exponent
Sign
Sub

Mux
Input 2
AddSub

84. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 84
12.4 Other Floating-Point Operations
Floating-point multiplication
(2e1s1)  (2e2s2) = 2e1+e2(s1  s2)
Product of significands in [1, 4)
If product is in [2, 4), halve to normalize (increment exponent)
Floating-point division
(2e1s1) / (2e2s2) = 2e1–e2(s1 / s2)
Ratio of significands in (1/2, 2)
If ratio is in (1/2, 1), double to normalize (decrement exponent)
Floating-point square-rooting
(2es)1/2 = 2e/2(s)1/2 when e is even
= 2(e–1)2(2s)1/2 when e is odd
Normalization not needed
Overflow
(underflow)
possible
Overflow
(underflow)
possible

85. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 85
Hardware for
Floating-Point
Multiplication
and Division
Figure 12.6 Simplified
schematic of a floating-
point multiply/divide unit.
Normalize
& round
Multiply
or divide
Unpack
Control
& sign
logic
MulDiv
Pack
Input 1
Output
Significands
Exponents
Signs
Significand
Exponent
Sign


Input 2

86. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 86
12.5 Floating-Point Instructions
Floating-point arithmetic instructions for MiniMIPS:
add.s $f0,$f8,$f10 # set $f0 to ($f8) +fp ($f10)
sub.d $f0,$f8,$f10 # set $f0 to ($f8) –fp ($f10)
mul.d $f0,$f8,$f10 # set $f0 to ($f8) fp ($f10)
div.s $f0,$f8,$f10 # set $f0 to ($f8) /fp ($f10)
neg.s $f0,$f8 # set $f0 to –($f8)
Figure 12.7 The common floating-point instruction format for
MiniMIPS and components for arithmetic instructions. The extension
(ex) field distinguishes single (* = s) from double (* = d) operands.
x
x x
x
0
1
1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1
1
0 0 0 0
0 0 0 0
31 25 20 15 0
Floating-point
instruction
s = 0
d = 1
Source
register 2
op ex ft
F
fs fd
10 5
fn
Destination
register
add.* = 0
sub.* = 1
mul.* = 2
div.* = 3
neg.* = 7
Source
register 1

87. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 87
The Floating-Point Unit in MiniMIPS
Figure 5.1 Memory and processing subsystems for MiniMIPS.
Memory
up to 2 words
30
Loc 0 Loc 4 Loc 8
Loc
m 4
Loc
m 8
4 B / location
m  232
$0
$1
$2
$31
Hi Lo
ALU
$0
$1
$2
$31
FP
arith
EPC
Cause
BadVaddr
Status
EIU FPU
TMU
Execution
& integer
unit
Floating-
point unit
Trap &
memory
unit
. . .
. . .
(Coproc. 1)
(Coproc. 0)
(Main proc.)
Integer
mul/div
Chapter
10
Chapter
11
Chapter
12
Pairs of registers,
beginning with an
even-numbered
one, are used for
double operands
Coprocessor 1

88. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 88
Floating-Point Format Conversions
MiniMIPS instructions for number format conversion:
cvt.s.w $f0,$f8 # set $f0 to single(integer $f8)
cvt.d.w $f0,$f8 # set $f0 to double(integer $f8)
cvt.d.s $f0,$f8 # set $f0 to double($f8)
cvt.s.d $f0,$f8 # set $f0 to single($f8,$f9)
cvt.w.s $f0,$f8 # set $f0 to integer($f8)
cvt.w.d $f0,$f8 # set $f0 to integer($f8,$f9)
Figure 12.8 Floating-point instructions for format conversion in MiniMIPS.
1
0 0 x
x x
x
0
1
1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1
0 0 0 0
0 0 0
31 25 20 15 0
Floating-point
instruction
*.w = 0
w.s = 0
w.d = 1
*.* = 1
Unused
op ex ft
F
fs fd
10 5
fn
Destination
register
To format:
s = 32
d = 33
w = 36
Source
register

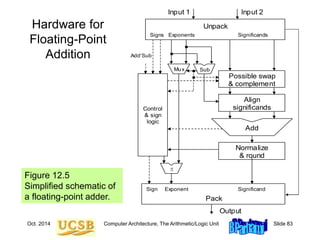
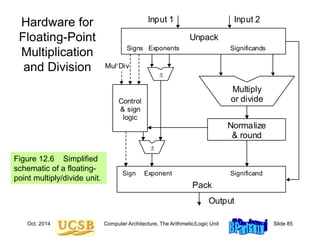
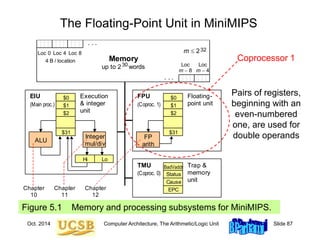
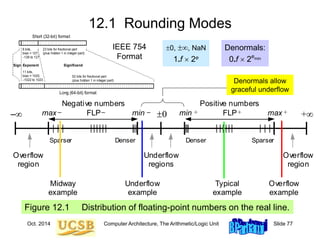
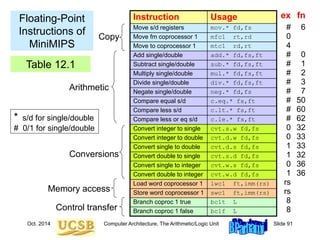
89. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 89
Floating-Point Data Transfers
MiniMIPS instructions for floating-point load, store, and move:
lwc1 $f8,40($s3) # load mem[40+($s3)] into $f8
swc1 $f8,A($s3) # store ($f8) into mem[A+($s3)]
mov.s $f0,$f8 # load $f0 with ($f8)
mov.d $f0,$f8 # load $f0,$f1 with ($f8,$f9)
mfc1 $t0,$f12 # load $t0 with ($f12)
mtc1 $f8,$t4 # load $f8 with ($t4)
Figure 12.9 Instructions for floating-point data movement in MiniMIPS.
0
1 1
0 0
x
0
1
1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1
0 0 0 0
0 0 0 0
31 25 20 15 0
Floating-point
instruction
s = 0
d = 1
Unused
op ex ft
F
fs fd
10 5
fn
Destination
register
mov.* = 6
Source
register
1 1
1 0 0
0
0
x
0
1
1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0
0 0
0 0 0
31 25 20 15 0
Floating-point
instruction
mfc1 = 0
mtc1 = 4
Unused
op rs rt
R
rd sh
10 5
fn
Destination
register
Source
register
Unused

90. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 90
Floating-Point Branches and Comparisons
MiniMIPS instructions for floating-point load, store, and move:
bc1t L # branch on fp flag true
bc1f L # branch on fp flag false
c.eq.* $f0,$f8 # if ($f0)=($f8), set flag to “true”
c.lt.* $f0,$f8 # if ($f0)<($f8), set flag to “true”
c.le.* $f0,$f8 # if ($f0)($f8), set flag to “true”
Figure 12.10 Floating-point branch and comparison instructions in MiniMIPS.
x
0
0
1
0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1
0 0
1 1
0 0 0 0 0 0
31 25 20 15 0
Floating-point
instruction
true = 1
false = 0
bc1? = 8 Offset
op rs rt operand / offset
I
1 0 0
1 1
0 0
x
0
1
1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0
0 0 0
31 25 20 15 0
Floating-point
instruction
s = 0
d = 1
Source
register 2
op ex ft
F
fs fd
10 5
fn
Unused c.eq.* = 50
c.lt.* = 60
c.le.* = 62
Source
register 1
Correction: 1 1 x x x 0

91. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 91
Floating-Point
Instructions of
MiniMIPS
Instruction Usage
Move s/d registers mov.* fd,fs
Move fm coprocessor 1 mfc1 rt,rd
Move to coprocessor 1 mtc1 rd,rt
Add single/double add.* fd,fs,ft
Subtract single/double sub.* fd,fs,ft
Multiply single/double mul.* fd,fs,ft
Divide single/double div.* fd,fs,ft
Negate single/double neg.* fd,fs
Compare equal s/d c.eq.* fs,ft
Compare less s/d c.lt.* fs,ft
Compare less or eq s/d c.le.* fs,ft
Convert integer to single cvt.s.w fd,fs
Convert integer to double cvt.d.w fd,fs
Convert single to double cvt.d.s fd,fs
Convert double to single cvt.s.d fd,fs
Convert single to integer cvt.w.s fd,fs
Convert double to integer cvt.w.d fd,fs
Load word coprocessor 1 lwc1 ft,imm(rs)
Store word coprocessor 1 swc1 ft,imm(rs)
Branch coproc 1 true bc1t L
Branch coproc 1 false bc1f L
Copy
Control transfer
Conversions
Arithmetic
Memory access
ex
#
0
4
#
#
#
#
#
#
#
#
0
0
1
1
0
1
rs
rs
8
8
fn
6
0
1
2
3
7
50
60
62
32
33
33
32
36
36
Table 12.1
* s/d for single/double
# 0/1 for single/double

92. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 92
12.6 Result Precision and Errors
Example 12.4
Laws of algebra may not hold in floating-point arithmetic. For example,
the following computations show that the associative law of addition,
(a + b) + c = a + (b + c), is violated for the three numbers shown.
Compute a + b
2  0.00000011
a+b = 2  1.10000000
c =-2  1.01100101
Numbers to be added first
a =-2  1.10101011
b = 2  1.10101110
5
5
Compute (a + b) + c
2  0.00011011
Sum = 2  1.10110000
5
2
2
2
6
Compute b + c (after preshifting c)
2  1.101010110011011
b+c = 2  1.10101011 (Round)
a =-2  1.10101011
Numbers to be added first
b = 2  1.10101110
c =-2  1.01100101
5
5
Compute a + (b + c)
2  0.00000000
Sum = 0 (Normalize to special code for 0)
5
5
5
2

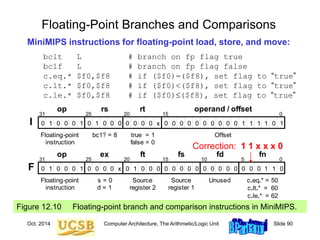
93. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 93
Error Control and Certifiable Arithmetic
Catastrophic cancellation in subtracting almost equal numbers:
Area of a needlelike triangle
A = [s(s – a)(s – b)(s – c)]1/2
Possible remedies
Carry extra precision in intermediate results (guard digits):
commonly used in calculators
Use alternate formula that does not produce cancellation errors
Certifiable arithmetic with intervals
A number is represented by its lower and upper bounds [xl, xu]
Example of arithmetic: [xl, xu] +interval [yl, yu] = [xl +fp yl, xu +fp yu]
a
b
c

94. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 94
Evaluation of Elementary Functions
Approximating polynomials
ln x = 2(z + z3/3 + z5/5 + z7/7 + . . . ) where z = (x – 1)/(x + 1)
ex = 1 + x/1! + x2/2! + x3/3! + x4/4! + . . .
cos x = 1 – x2/2! + x4/4! – x6/6! + x8/8! – . . .
tan–1 x = x – x3/3 + x5/5 – x7/7 + x9/9 – . . .
Iterative (convergence) schemes
For example, beginning with an estimate for x1/2, the following
iterative formula provides a more accurate estimate in each step
q(i+1) = 0.5(q(i) + x/q(i))
Table lookup (with interpolation)
A pure table lookup scheme results in huge tables (impractical);
hence, often a hybrid approach, involving interpolation, is used.

95. Oct. 2014 Computer Architecture, The Arithmetic/Logic Unit Slide 95
Figure 12.12 Function evaluation by table lookup and linear interpolation.
Function Evaluation by Table Lookup
L
Add
x
Table
for a
Output
Table
for b
x
Input x
H L
f(x)
Multiply
h bits k - h bits
xH
f(x)
x
x
Best linear
approximation
in subinterval
The linear approximation above is
characterized by the line equation
a + b x , where a and b are
read out from tables based on x
L
H