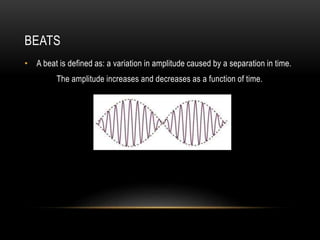
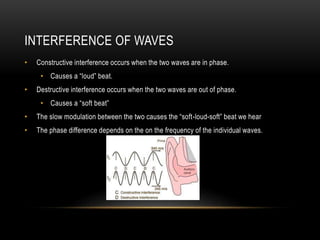
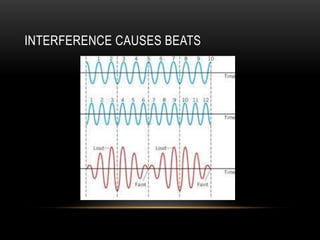
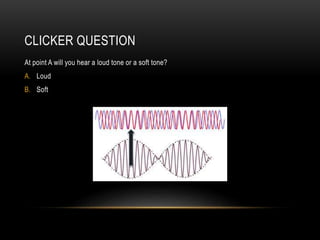
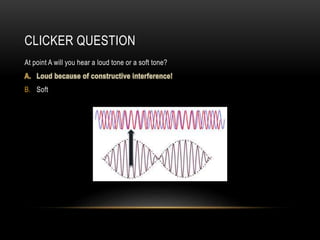
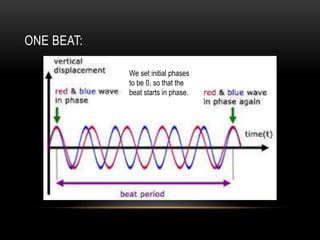
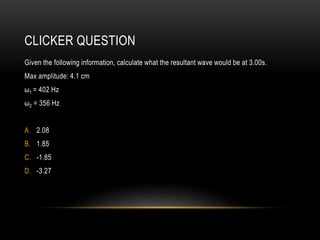
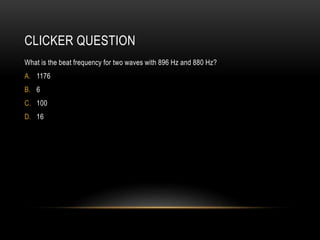
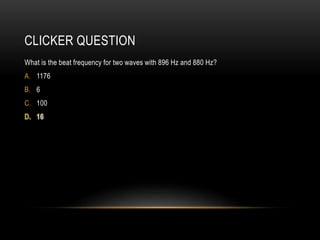
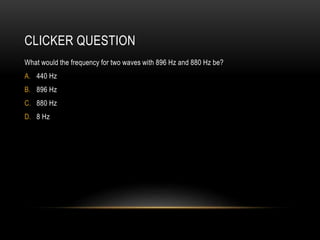
Beats occur when two sounds waves with slightly different frequencies interfere. The amplitude of the resulting sound wave varies over time between constructive and destructive interference of the original waves. If the frequency difference is small, a single tone is heard that modulates in amplitude at the beat frequency. If the difference is large, two distinct tones are heard. Beats can be calculated using equations that account for the mean frequency and difference between the original frequencies.

1. INTERFERENCE AND BEATS

2. BEATS
• A beat is defined as: a variation in amplitude caused by a separation in time.
The amplitude increases and decreases as a function of time.

3. AMPLITUDE AND FREQUENCY
• The rate at which the amplitude varies is proportional to the frequency difference.
• If the frequency difference is large  we hear two different tones that vary in
intensity
• If the frequency difference is small  we hear a tone that has a mean frequency
and the amplitude varies by the difference in angular frequency

4. CLICKER QUESTION
In which of the following sets of frequencies will you be able to hear two distinct tones?
A. 647 Hz and 843 Hz
B. 567 Hz and 558 Hz
C. 221 Hz and 224 Hz
D. 746 Hz and 735 Hz

5. CLICKER QUESTION
In which of the following sets of frequencies will you be able to hear two distinct tones?
B. 567 Hz and 558 Hz
C. 221 Hz and 224 Hz
D. 746 Hz and 735 Hz

6. CLICKER QUESTION
If two waves are oscillating at 445 Hz and 452 Hz, will you hear a single tone or two distinct
tones and with what frequency?
A. Two, 448.5 Hz
B. Single, 448.5 Hz
C. Two, 445 Hz
D. Single, 445 Hz
E. Single 450 Hz

7. CLICKER QUESTION
If two waves are oscillating at 445 Hz and 452 Hz, will you hear a single tone or two distinct
tones and with what frequency?
A. Two, 448.5 Hz
C. Two, 445 Hz
D. Single, 445 Hz
E. Single 450 Hz

8. INTERFERENCE OF WAVES
• Constructive interference occurs when the two waves are in phase.
• Causes a “loud” beat.
• Destructive interference occurs when the two waves are out of phase.
• Causes a “soft beat”
• The slow modulation between the two causes the “soft-loud-soft” beat we hear
• The phase difference depends on the on the frequency of the individual waves.

9. INTERFERENCE CAUSES BEATS

10. CLICKER QUESTION
At point A will you hear a loud tone or a soft tone?
A. Loud
B. Soft

11. CLICKER QUESTION
At point A will you hear a loud tone or a soft tone?
B. Soft

12. RESULTANT WAVES
• The resultant wave can be calculated using the principle of superposition and the
following equations
• MEAN ANGULAR FREQUENCY: ϖ = (ω1 + ω2 ) / 2
• ANGULAR FREQUENCY DIFFERNCE: Δω = (ω1 – ω2) / 2
• Stotal (0, t) = 2smcos(- ϖ t)cos(- Δω t)
• = 2smcos( ϖ t)cos( Δω t)
• From this equation we conclude that one wave oscillates with a mean frequency,
while the other oscillates with the angular frequency difference.

13. ONE BEAT:
We set initial phases
to be 0, so that the
beat starts in phase.

14. CLICKER QUESTION
Given the following information, calculate what the resultant wave would be at 3.00s.
Max amplitude: 4.1 cm
ω1 = 402 Hz
ω2 = 356 Hz
A. 2.08
B. 1.85
C. -1.85
D. -3.27

15. CLICKER QUESTION
Given the following information, calculate what the resultant wave would be at 3.00s.
Max amplitude: 4.1 cm
ω1 = 402 Hz
ω2 = 356 Hz
A. 2.08
C. -1.85
D. -3.27

16. BEAT FREQUENCY
• Beat frequency is calculated by the difference between the two frequencies given.

17. CLICKER QUESTION
What is the beat frequency for two waves with 896 Hz and 880 Hz?
A. 1176
B. 6
C. 100
D. 16

18. CLICKER QUESTION
What is the beat frequency for two waves with 896 Hz and 880 Hz?
A. 1176
B. 6
C. 100

19. CLICKER QUESTION
What would the frequency for two waves with 896 Hz and 880 Hz be?
A. 440 Hz
B. 896 Hz
C. 880 Hz
D. 8 Hz

20. CLICKER QUESTION
What would the frequency for two waves with 896 Hz and 880 Hz be?
B. 896 Hz
C. 880 Hz
D. 8 Hz