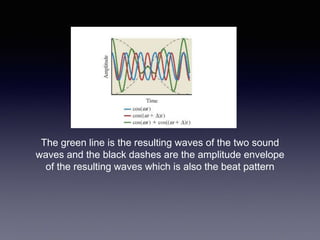
Beats occur when two sounds waves with similar frequencies are combined. The frequency of the beats is equal to the difference between the frequencies of the two sound waves. If a violin player hears 2 beats per second while tuning a string, the untuned string's frequency must be 2 Hz lower than the reference frequency of 440 Hz. For two animals calling from land and water, the beat frequency is calculated using their wavelengths to determine frequencies, then taking the difference, which is 5.5 Hz.

1. BEATS

2. Beats are the result of when two sinusoidal sound
waves with equal amplitude and almost same
frequencies are combined with each other.
What is Beat?

3. The green line is the resulting waves of the two sound
waves and the black dashes are the amplitude envelope
of the resulting waves which is also the beat pattern

4. If 2 or more sounds with difference
of frequency of 20-30 Hz, the
frequency of beats is the difference
of frequencies of waves.
Frequency of Beats

5. If the frequency difference
is larger 20 o 30 Hz, beats
are not observed.
Frequency of Beats

6. The frequency of two sounds interfering
with each other (with similar frequencies)
is the average of the two frequencies of
the two sinusoidal sound waves
Frequency of The Resulting

7. A violin player is using one of the
string on a previous tuned violin to tune one of his string.
The previous tune violin produces a frequency of 440 Hz.
When tuning, the player heard 2 beats per second. The
player tuned it by increasing the tension of the string
Question #1
a) What is the frequency of the untuned
string?

8. We know that the frequency of beats is the
difference of frequencies of waves. And since the
player heard a beat of 2 Hz. The untuned string is
either 440 Hz - 2Hz = 438 Hz or 440 Hz + 2 Hz =
442Hz. However, the player tuned it by increasing
the tension of the string ( higher frequency) we
know that the untuned string has a lower
frequency than the tuned string. So the answer is
438 Hz.
Solution:

9. Two animals are in close approximating. One animal is
shouting into open air while the other one is shouting
from inside the water. The animal on the land shouting
in the open air produced a wavelength of 5m while the
animal shouting from the water created a wavelength
of 20m. Will it produce beat? If so what is the beat
frequency of the combing two sounds?
Question #2

10. First, we need to find out the frequency of the two
sound waves. We can do this by using f=v/λ.
We know the velocity of the sound of screaming
animal on the land is 343 m/s (speed of sound in
air) and the velocity of sound of screaming animal
in the water is 1482 m/s ( speed of sound in
water). And we know the wavelength for both the
sound waves.

11. The frequency of the land animal :
f=v/λ ( f= 343/ 5 = 68.6 Hz)
Frequency of the aqueous animal:
f=v/λ ( f= 1482/ 20 = 74.1 Hz)

12. We know that a beat will be created because the
difference of the two sound waves is less than 20 .
Since the frequency of the beat is equal to the
difference of frequency between the two sound
waves. So the frequency of beat = 74.1 Hz - 68.6
Hz = 5.5 Hz