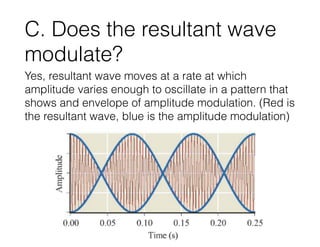
The document discusses beats, which occur when two sounds with similar frequencies interact. Beats are heard as a modulation in volume as the waves alternately interfere constructively and destructively. When trying to tune a flute to a tuner emitting 440Hz, but the flute is playing at 434Hz, beats will be heard at a frequency of 6Hz as the two tones modulate together. The overall tone heard will be the average frequency of 437Hz.

1. BEATS

2. What is a Beat?
• A beat occurs when two waves with very similar frequencies interact
• The rate at which the resultant wave amplitude increases and decreases
as a function of time is proportional to the difference in angular frequency
• When the frequency difference is large, we hear the sound as two distinct
tones
• When the frequency difference is small, we hear beats
• In a graph, we would see the two frequencies falling out of phase with
destructive interference and back in phase with constructive interference
• In a graph, the resultant wave oscillates by increasing and decreasing in
amplitude, which we call modulated, and creates the beating effect

3. Observing Beats for a Fixed
Location in Space
• The two waves we will consider have the same amplitude, but different frequencies,
wavelengths, and wave numbers
• We set phases to 0, apply the principle of superposition, and set x=x0=0 to add the two
waves.
sTotal=(x0,t)=s1(x0,t)+s2(x0,t)
=smcos(k1x0-w1t)+smcos(k2x0-w2t)
=2sm(1/2)cos(k1x0-w1t+k2x0-w2t)x(1/2)cos(k1x0-w1t-k2x0+w2t)]
=2smcos[((k1+k2)/2)x0-[((w1+w2)/2)t]xcos[((k1-k2)/2)x0-[((w1-w2)/2)t]
mean angular frequency=wmean=(w1+w2)/2
angular frequency difference=∆w=(w1-w2)/2
sTotal=(0,t)=2smcos(wmean)cos(∆w)

4. You are trying to tune your flute. Your tuner
emits the in-tune frequency of A4 at 440Hz
for you to imitate to tune your flute.
However, since your flute is not in tune and
the two frequencies differ slightly when the
tuner emits 440Hz in the background while
you play A4 at 434Hz…
A. Do you hear a beat? How do you know?
B. What is the tone that you hear?
C. Does the resultant wave modulate?
D. What is the beat frequency?

5. A. Do you hear a beat? How
do you know?
Yes! Since the frequencies are not the same
and do not have a significant difference,
their waves will interact to form a rate at
which amplitude varies and a frequency
difference that is small enough to cause our
ears to detect one tone instead of two.

6. B. What is the tone that you
hear?
The tone we will hear is the mean angular frequency
given by wmean=(w1+w2)/2.
wmean=(440Hz+434Hz)/2
wmean=437Hz

7. C. Does the resultant wave
modulate?
Yes, resultant wave moves at a rate at which
amplitude varies enough to oscillate in a pattern that
shows and envelope of amplitude modulation. (Red is
the resultant wave, blue is the amplitude modulation)

8. D. What is the beat
frequency?
The beat frequency is given to us by ∆w=(w1-w2)/2. This
equation is intended to modulate the amplitude of the resultant
wave, which usually has a smaller positive and negative crests.
However, the resultant wave modulates and the modulation
amplitude have greater positive and negative crests. This
means the beat frequency is only the difference between the
two frequencies.
∆w=(w1-w2)
∆w=(440Hz-434Hz)
∆w=6Hz