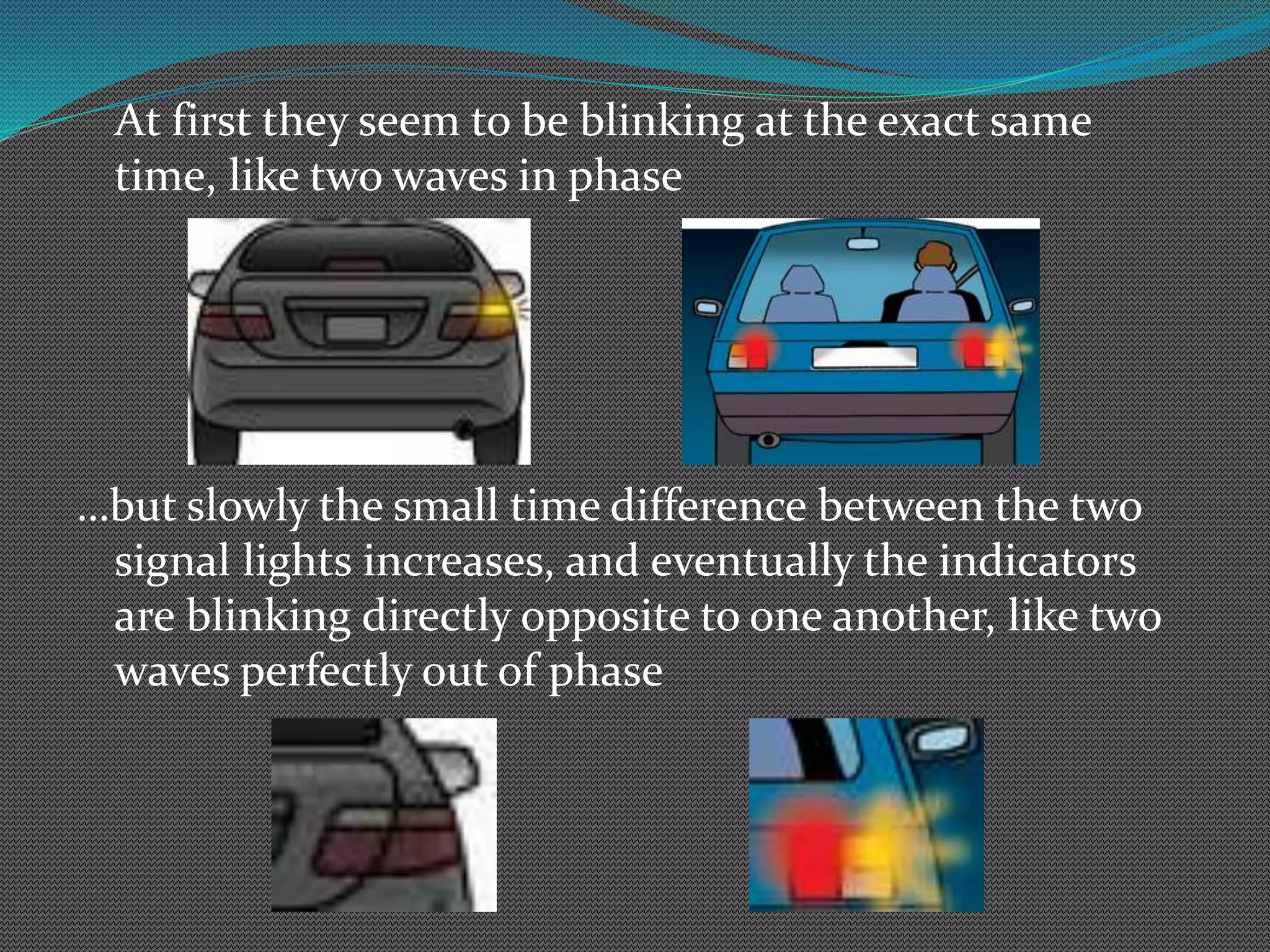
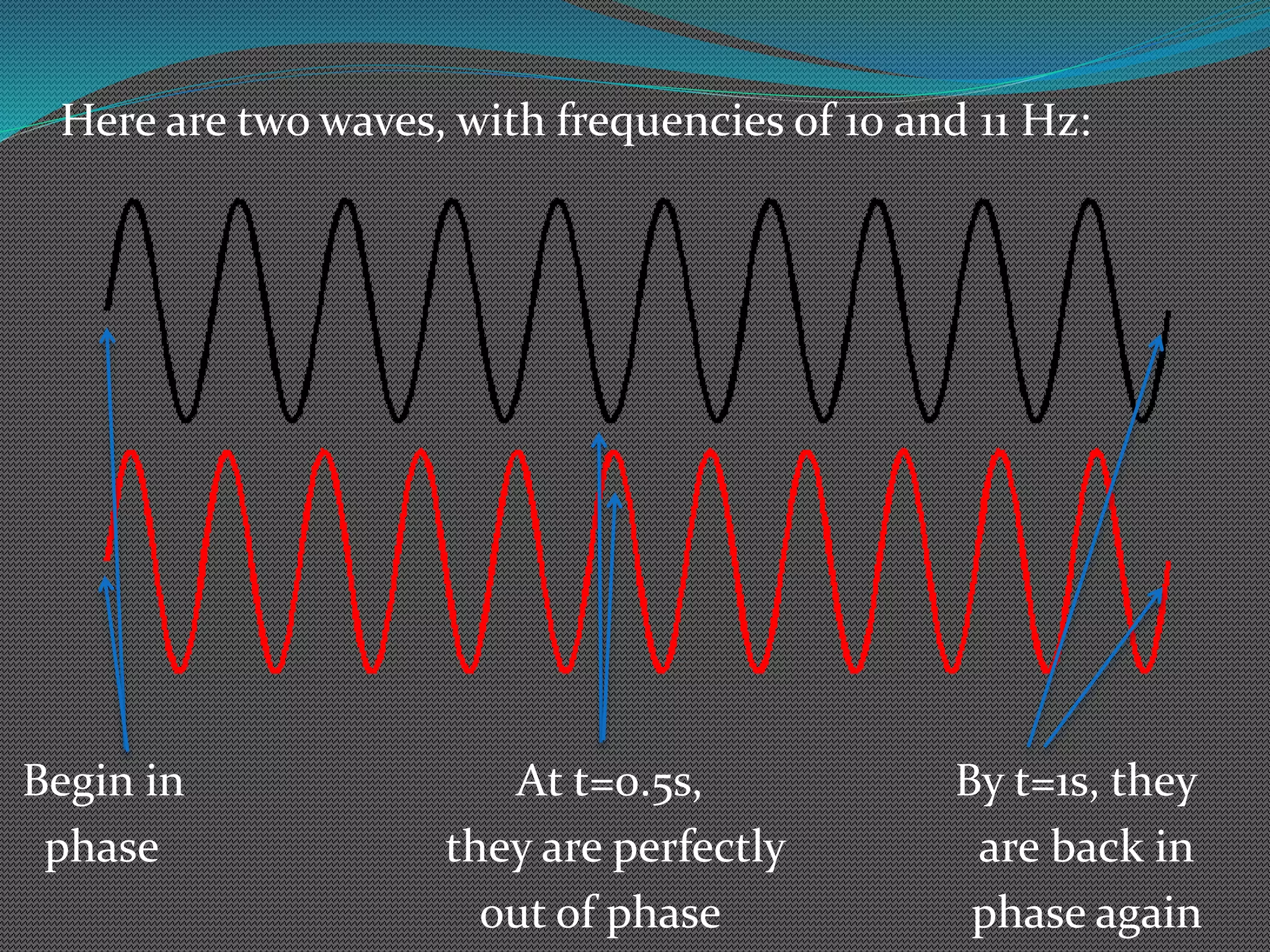
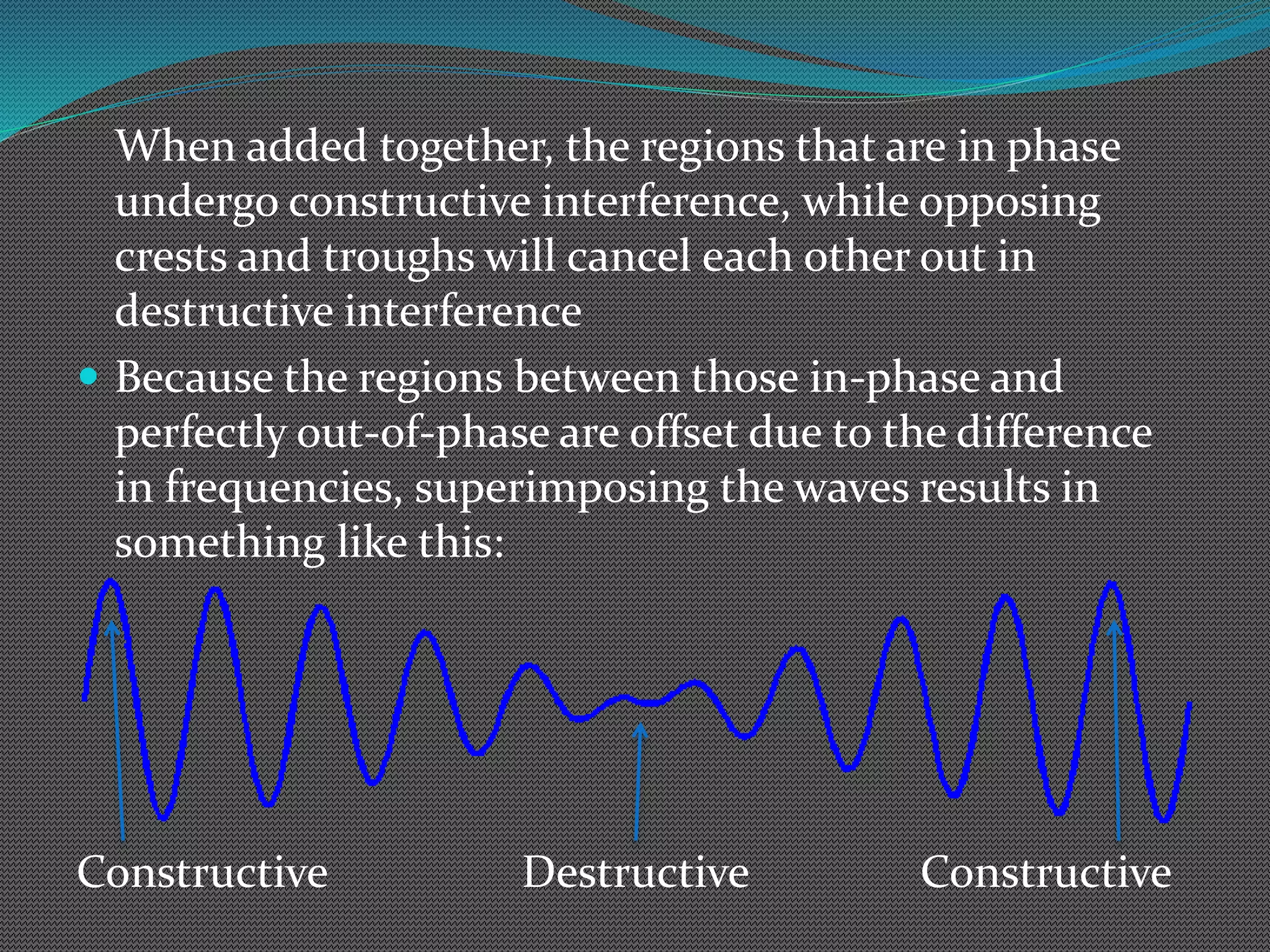
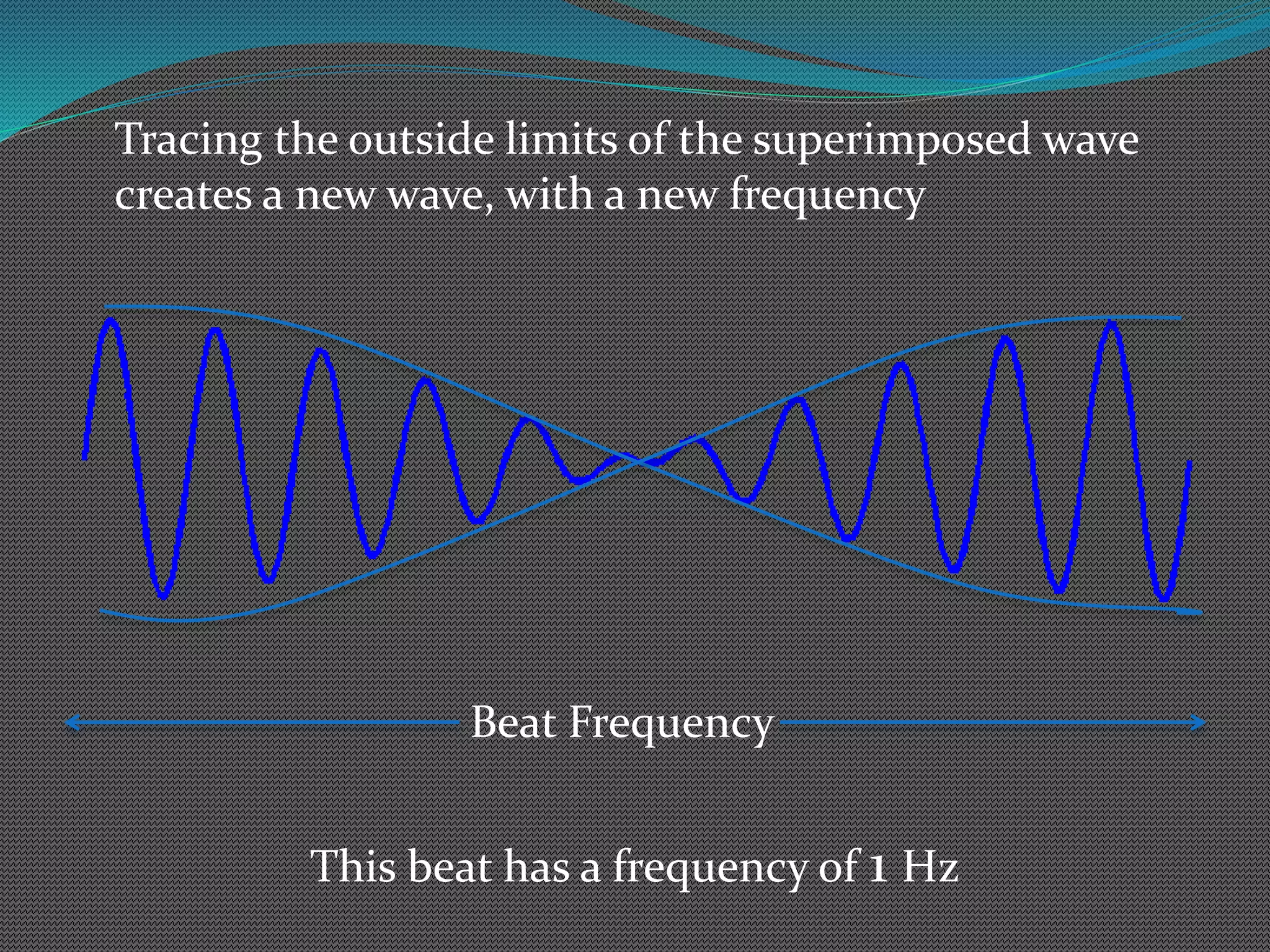
This document explains what beats are and how they are created by the interference of two waves with different frequencies. When two waves with frequencies of 10 Hz and 11 Hz are superimposed, they will oscillate between constructive and destructive interference, creating a new wave with a frequency of 1 Hz called the beat frequency. The beat frequency is calculated by taking the absolute value of the difference between the two original frequencies. As an example, two sound waves with frequencies of 35 Hz and 39 Hz will produce a beat with a frequency of 4 Hz.

2. What is a beat?
Have you ever been stopped at a red light in a car,
waiting to turn, and noticed that your indicator light is
blinking at a slightly different tempo than the car in
front of you?

3. At first they seem to be blinking at the exact same
time, like two waves in phase
…but slowly the small time difference between the two
signal lights increases, and eventually the indicators
are blinking directly opposite to one another, like two
waves perfectly out of phase

4. Why do beats occur?
This oscillation between blinking together, opposite,
and eventually together again, parallels how two waves
with different frequencies create “beats” when
superimposed

5. Here are two waves, with frequencies of 10 and 11 Hz:
Begin in At t=0.5s, By t=1s, they
phase they are perfectly are back in
out of phase phase again

6. When added together, the regions that are in phase
undergo constructive interference, while opposing
crests and troughs will cancel each other out in
destructive interference
 Because the regions between those in-phase and
perfectly out-of-phase are offset due to the difference
in frequencies, superimposing the waves results in
something like this:
Constructive Destructive Constructive

7. Tracing the outside limits of the superimposed wave
creates a new wave, with a new frequency
Beat Frequency
This beat has a frequency of 1 Hz

8. Beat Frequency
*The frequency of the beat is directly linked to the
frequencies of the two waves used to create it
Our two waves had frequencies of 10 and 11 Hz, and
when added together, the beat they created has a
frequency of 1 Hz
So, the beat frequency (fb) = fwave 2- fwave 1

9. Because frequency cannot be negative, the formula for
beat frequency becomes:
fb = |f2 – f1|
This formula can be used to find the frequency for any
beat, given the frequencies of the two original waves

10. Let’s Practice
Two sound waves travelling in the same direction with
frequencies of 35 and 39 Hz are superimposed.
 What is the frequency of the beat created?

11.  We know that both waves are sound waves, so they
both have a wave speed of ~343 m/s
 The question states that the frequencies of the waves
differ from one another, so knowing that their wave
speeds are the same, and remembering the formula
V = fλ
we know that their wavelengths must also be the same
** Frequency is the only thing that is different between
the two original waves

12. The only thing left to do is to apply the formula:
fb = |f2-f1|
= |39-35|
= 4
The beat has a frequency of 4 Hz

13. Image Sources
 http://ineke.co.uk/category/my-big-ideas/
 http://www.shutterstock.com/pic-162551174/stock-
vector-driver-education-car-rear-indicators-with-
headlights-off-day-time.html?src=-t6tes-ri--
sjJ4_6BW8CQ-1-6
 http://www.phys.uconn.edu/~gibson/Notes/Section5_
5/Sec5_5.htm