1. The document provides information about linear programming including definitions of key terms, steps to solve linear programming problems, examples worked out in detail, and exercises.
2. Linear programming involves optimizing (maximizing or minimizing) an objective function subject to certain constraints. It was first introduced by a Russian mathematician in the 1930s-1940s to optimize resources like manpower and materials during war time.
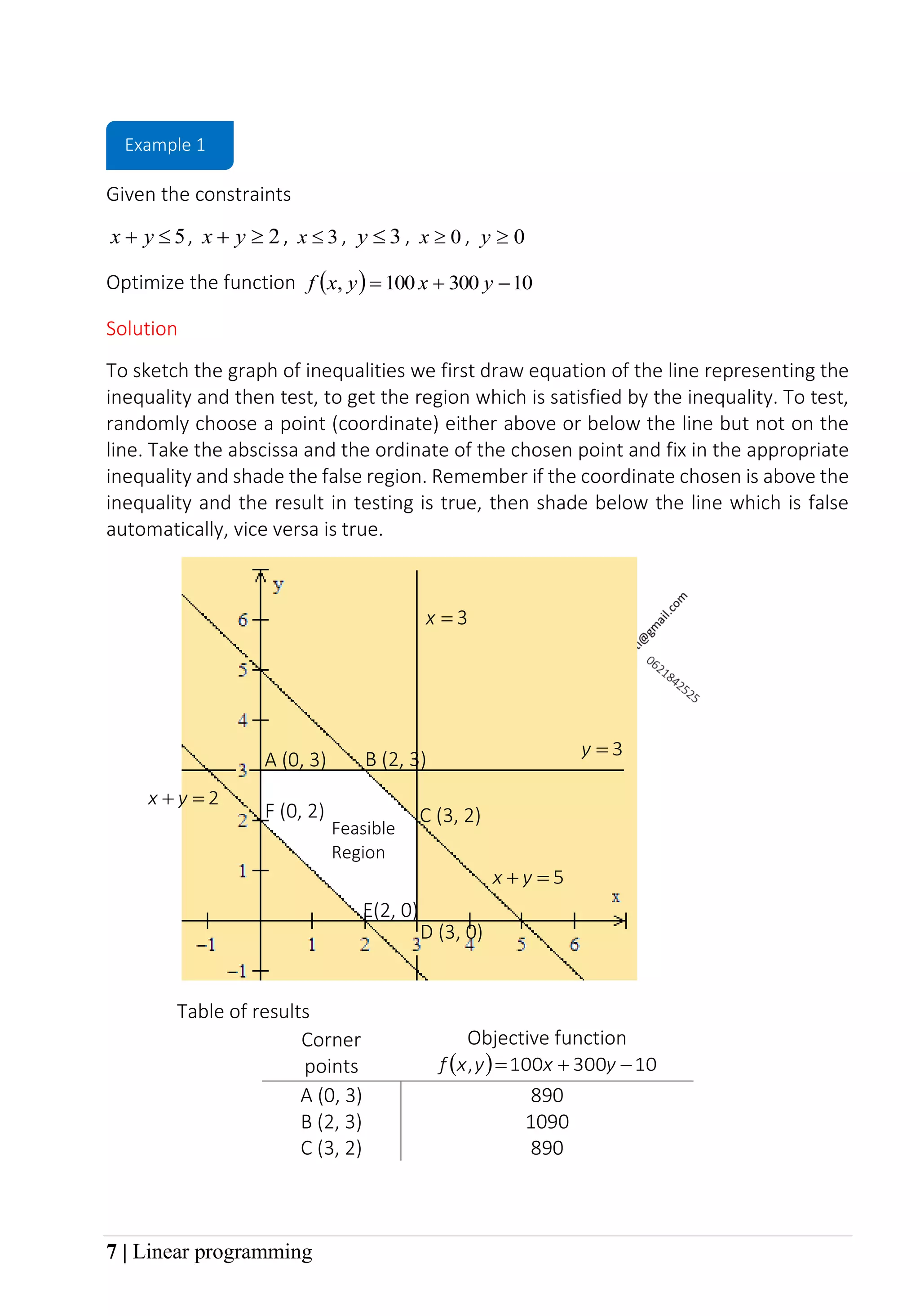
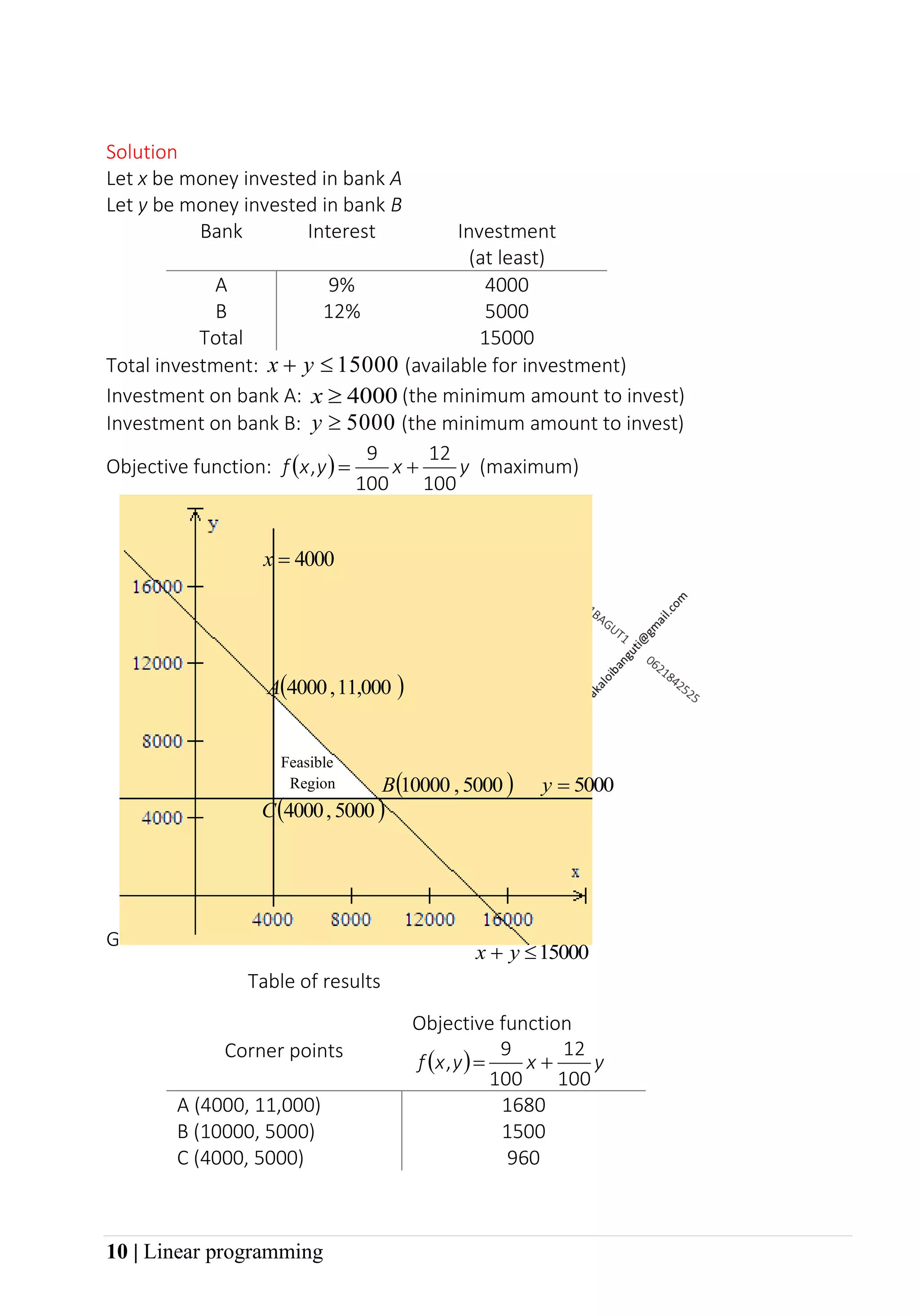
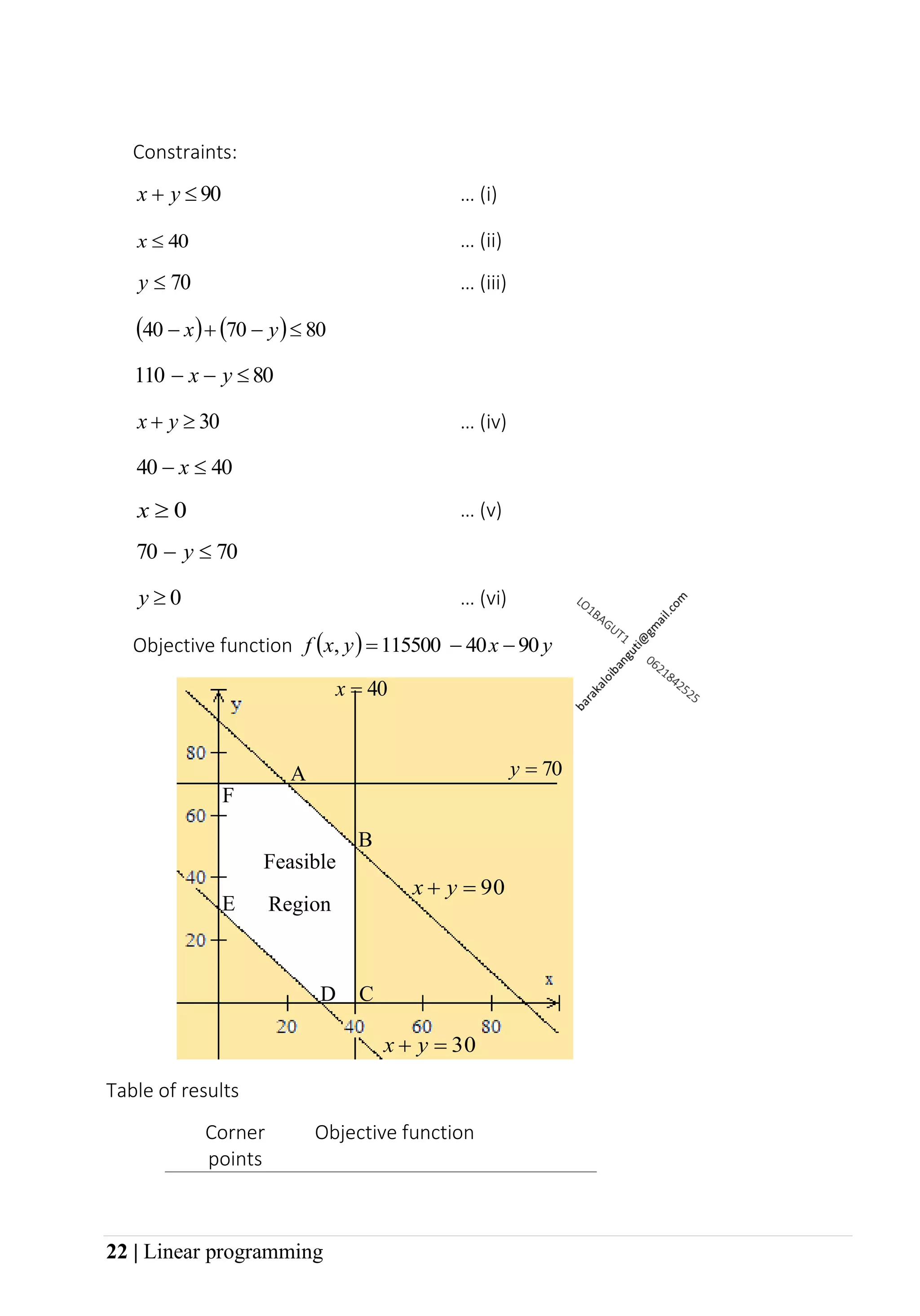
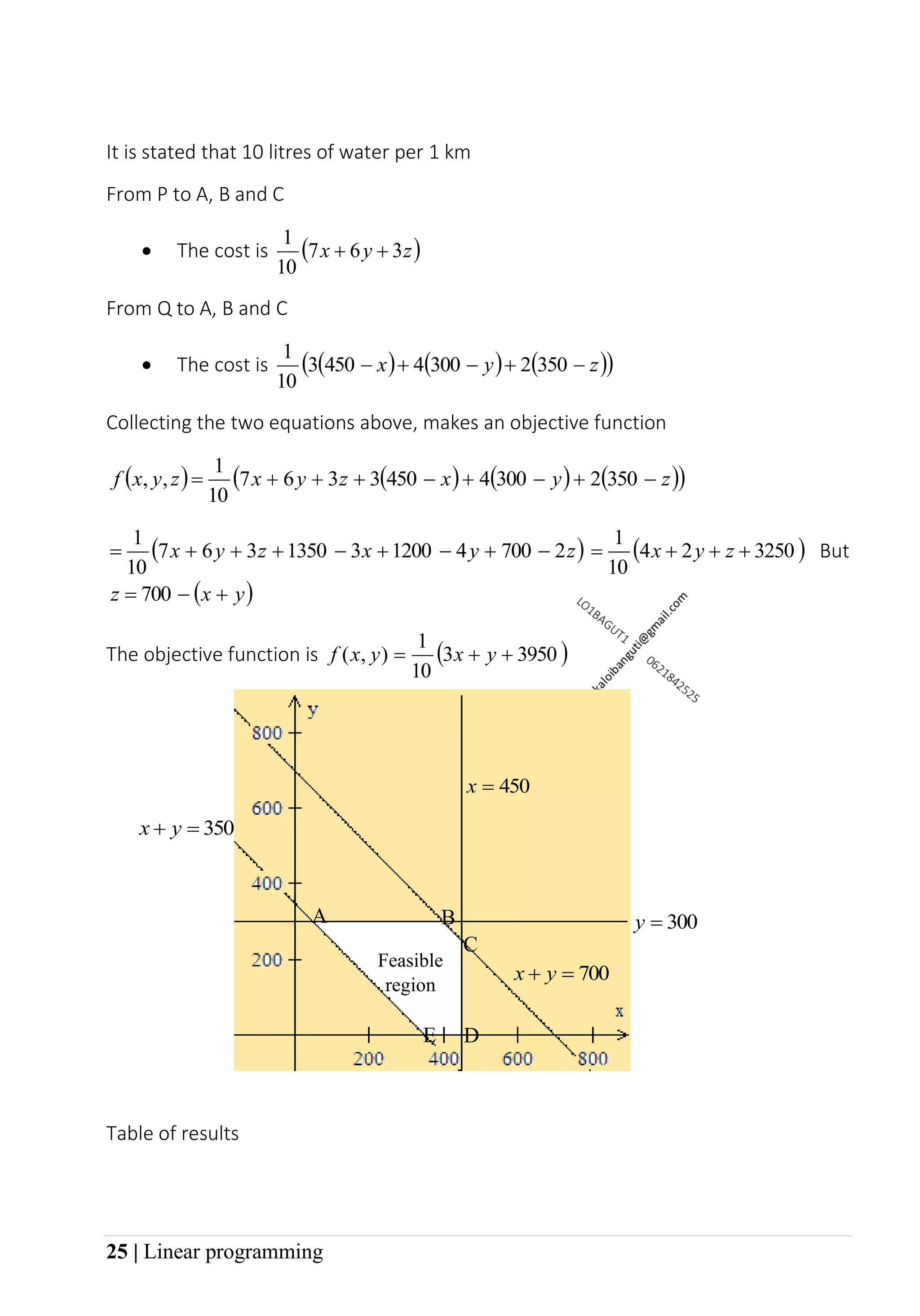
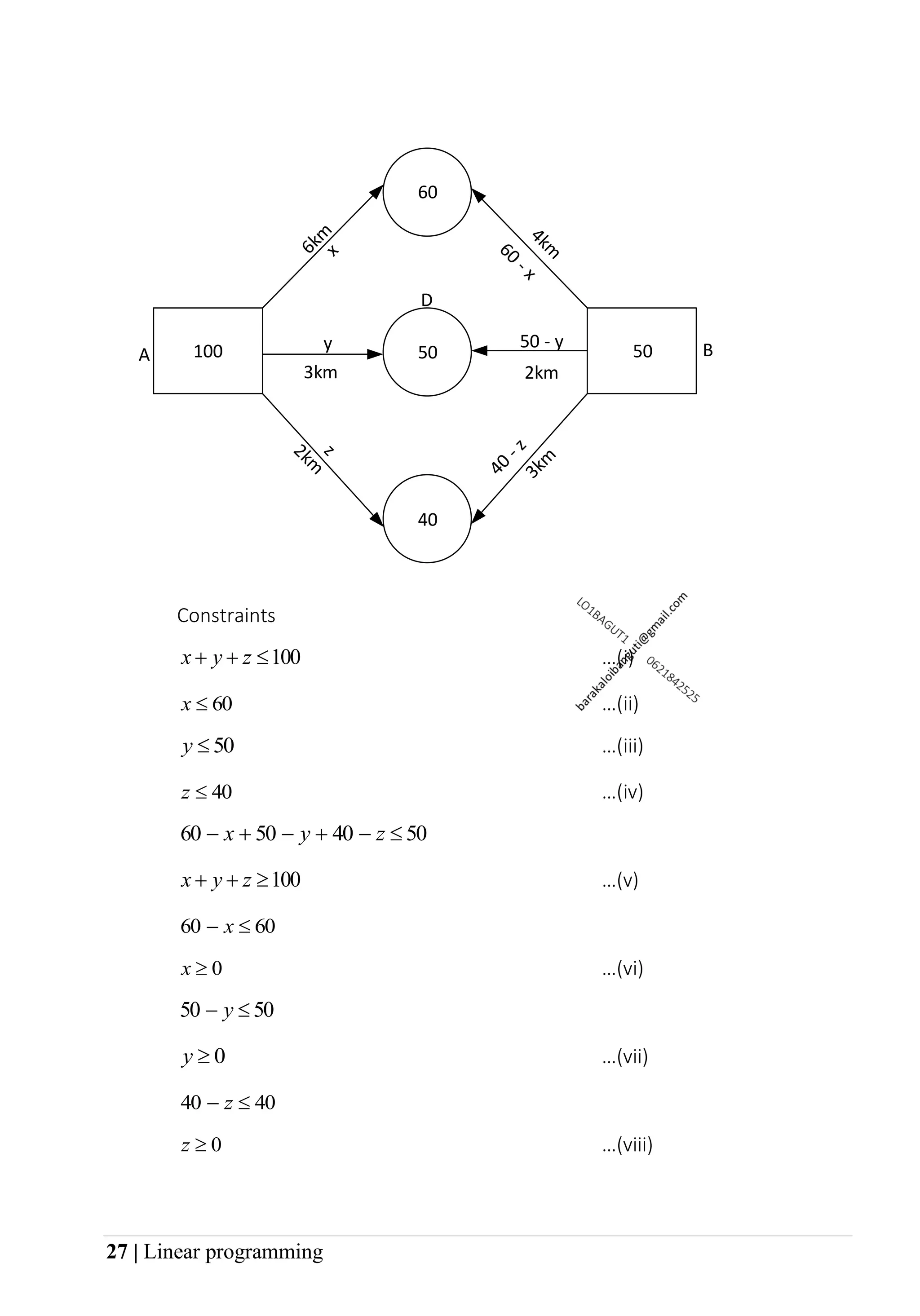
3. Examples worked out in the document show how to set up the constraints and objective function mathematically based on word problems, sketch the feasible region, find the corner points, and determine the optimal solution that maximizes or minimizes the objective function.