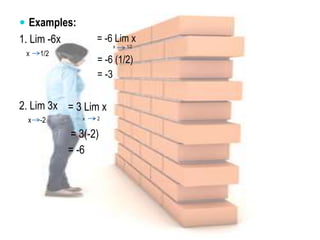
1. The document discusses limits of functions and different limit theorems. It defines a limit of a function as the intended height of a function and describes the behavior of the function at a specific x value. 2. The main limit theorems covered are: the limit of a constant, the limit of a function x, the limit of a constant and function f(x), and the limit of a sum and difference of functions. Examples are provided for each theorem. 3. Exercises are provided to evaluate limits using each theorem, including evaluating specific limits, explaining the steps, and simplifying. The document serves as a guide to understanding and applying different limit theorems.

2. What is your
limitation and
weakness in life?

3. “Nobody is perfect” as what we
always say. We have our own
strengths, but also do have our own
weakness and limitations. We commit
mistakes at times. But as God’s
creations, we continuously strive for
perfection. We all strive to act as
children of God. We all strive to reach
for the kingdom of God.

4. Limits of Functions by
Different Limit
Theorems

5. Limit of Function
 is the intended height of a
function.
It describes the behavior of
the function at a specific value
of x, which is the independent
variable.

6. Main Limit Theorems
In the definition of each theorem, let c be any constant, n as any
positive integer, and f and g as the given functions, which have
limits at k.
1. Limit of a Constant Theorem
Definition: Lim c = c
x k
Remember:
The limit of a constant as x approaches to any constant is
always equal to the given constant.
 Examples:
1. Lim -3
x 4
2. Lim 2/5
x 1/2

7. 2. Limit of a Function x
Definition: Lim x = k
x k
Remember:
The limit of the function x as x approaches to any
constant is always equal to the constant.
Examples:
1. Lim x
x 1
2.Lim x
x -1/2

8. 3. Limit of a Constant and a Function f(x)
Definition: Lim Lim cf(x) = c Lim Lim
x k x k
In Evaluating the Limit of a Constant and a Function,
the following steps can be followed:
a. Express the limit as a product of a constant and the
limit of a function x.
b. Find the limit of the function x based on the given
value for x.
c. Simplify the resulting numbers.

9.  Examples:
1. Lim -6x
x 1/2
2. Lim 3x
x -2
= -6 Lim x
x 1/2
= -6 (1/2)
= -3
= 3 Lim x
x - 2
= 3(-2)
= -6

10. 4. Limit of Sum and Difference of Functions
Definition: Lim [f(x) ± g(x)] = Lim f(x) ± Lim g(x)
x k x k x k
In evaluating the Limit of Sum / Difference of
Functions, the following steps can be followed:
a. Express the limit as sum or difference of functions
depending on the number of terms.
b. Apply the previously discussed limit theorems in
finding the limit of each term.
c. Simplify.

11. Examples:
1. Lim x + 5
x -2
2. Lim 4x - 2
x -5
= Lim x + Lim 5
x -2 x -2
= -2 + 5
= 3
= 4 Lim x - Lim 2
x -5 x -5
= 4(-5) -2
= -20 – 2
= -22

12. EXERCISES:
A. Evaluate the following limits by applying the Limit of
a Constant Theorem.
1. Lim π 2. Lim 5.25
x 3 x 1.2
B. Evaluate the following limits by applying the Limit of
the function x.
3. Lim x 4. Lim x
x 3 x -35

13. C. Evaluate the following limits by applying the Limit of
a Constant and a Function f(x)
5. Lim -4x 6. Lim 10x
x 2 x -5
D. Evaluate the following limits by applying the Limit of
Sum and Difference of Functions
7. Lim -3x – 4 8. Lim 2x - 15
x 1/3 x -1

14. Activity: Answer the following.
A. Evaluate the following limits by applying the Limit of a Constant Theorem.
1. Lim -3 2. Lim 25 3. Lim
x 2 x 50 x -2
B. Evaluate the ff. limits by applying the Limits of the function x.
4. Lim x 5. Lim x 6. Lim x
x 143 x x 2π
C. Evaluate the ff. limits by applying the Limit of a Constant and a Function f(x).
7. Lim -8x 8. Lim 100x
x 64 x
D. Evaluate the ff. limits by applying the Limit of Sum and Difference of Functions.
9. Lim 3x + 5 10. Lim 4x - 10
x -2 x

15. Prepared by:
Ms. Ma. Karen Grace L. Enrique