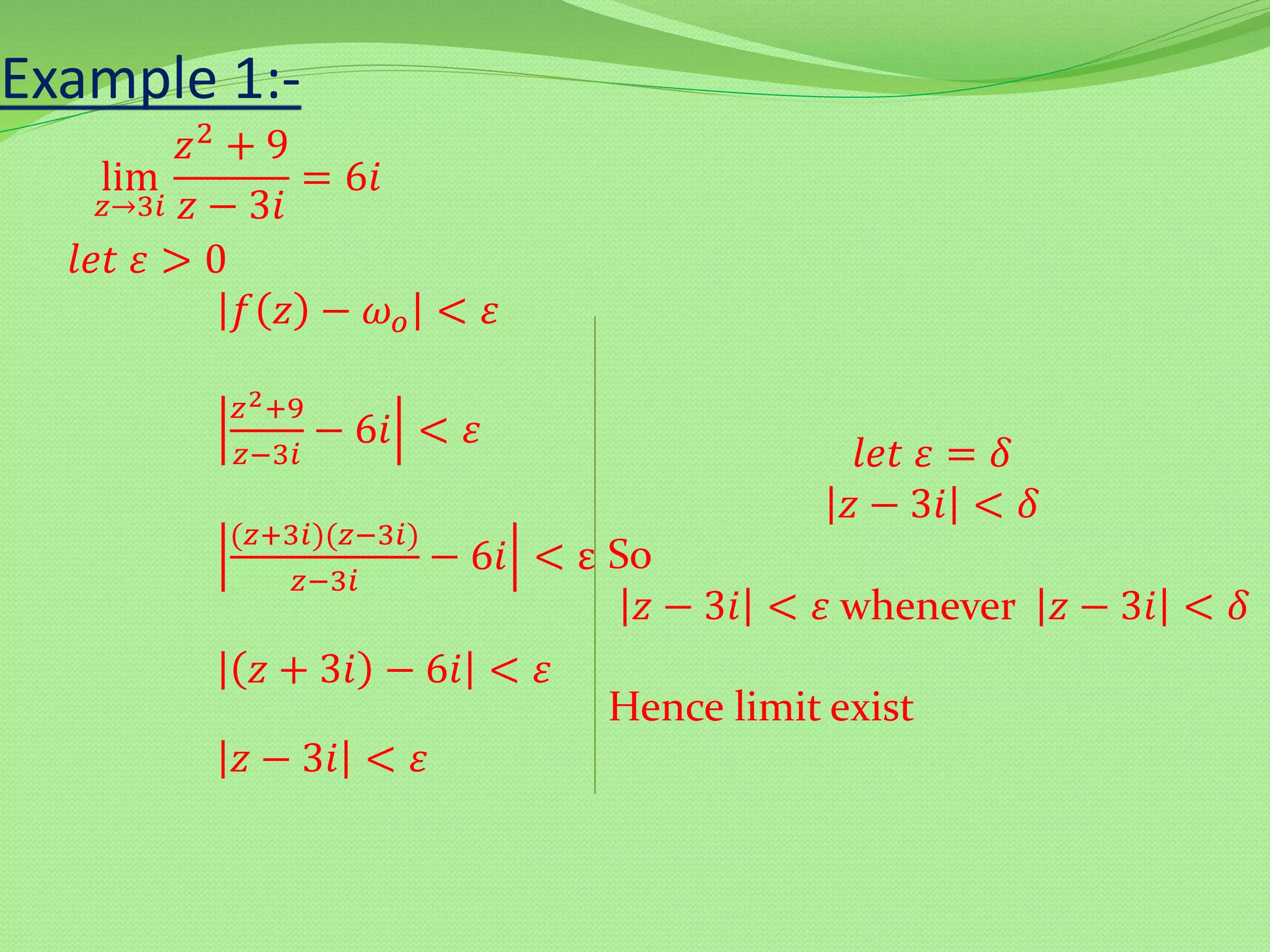The document lists the group members working on limits of complex functions. It then provides two definitions of limits - the first conceptual definition, and the second more precise "epsilon-delta" definition introduced by Bernard Bolzano in 1817. It explains that the epsilon refers to how close the function value needs to be to the limit, while delta refers to how close the input needs to be to still satisfy the epsilon condition. Some examples are then worked out to demonstrate the limit concept. Applications of limits in various engineering and science fields are discussed, such as fluid mechanics, mechanical design, astronomy, business, and medicine. It concludes by noting that what qualifies as "close enough" can depend on the context and precision needed.

4. Group Members:-
1. Umer Rashid (14093122-002)
2. Adnan Aslam (14093122-003)
3. Bilal Amjad (4093122-004)

5. Limits of complex functions
1st definition
Let f be a function of z. To say that
lim
𝑧→𝑧0
𝑓 𝑧 = 𝜔o
means that f (z) can be made arbitrarily close to 𝜔 𝑜 if we
choose the point z close enough to 𝑧 𝑜 but distinct from it.
We now express the definition of limit in a precise and
usable form.
How close is "close enough to 𝑧 𝑜 " depends on how close
one wants to make f(z) to 𝑤 𝑜.

6. 2nd definition
This definition is also known as "epsilon-delta
definition of limit“. It was first given by Bernard Bolzano
in 1817.
For a positive number ε, there is a positive number δ such
that
|f (z) − 𝜔 𝑜| < ε
whenever
0 < |z − 𝑧 𝑜| < δ.
Therefore let the positive number ε (epsilon) be how close
one wishes to make f(z) to 𝜔 𝑜, strictly one wants the
distance to be less than ε. Further, if the positive number δ
is how close one will make z to 𝑧 𝑜, and if the distance from
z to 𝑧 𝑜 is less than δ (but not zero), then the distance from
f(z) to 𝜔 𝑜 will be less than ε. Therefore δ depends on ε. The
limit statement means that no matter how small ε is made,
δ can be made small enough.

7. • The limit statement means that no matter how small ε
is made, δ can be made small enough.
• The letters ε and δ can be as "error" and "distance", and
in fact Cauchy used ε as an abbreviation for "error" in
some of his work. In these terms, the error (ε) in the
measurement of the value at the limit can be made as
small as desired by reducing the distance (δ) to the
limit point.

8. lim
𝑧→3𝑖
𝑧2 + 9
𝑧 − 3𝑖
= 6𝑖
𝑙𝑒𝑡 𝜀 > 0
𝑓 𝑧 − 𝜔 𝑜 < 𝜀
𝑧2+9
𝑧−3𝑖
− 6𝑖 < 𝜀
(𝑧+3𝑖)(𝑧−3𝑖)
𝑧−3𝑖
− 6𝑖 < ε
𝑧 + 3𝑖 − 6𝑖 < 𝜀
𝑧 − 3𝑖 < 𝜀
𝑙𝑒𝑡 𝜀 = 𝛿
𝑧 − 3𝑖 < 𝛿
So
𝑧 − 3𝑖 < 𝜀 whenever 𝑧 − 3𝑖 < 𝛿
Hence limit exist
Example 1:-

9. Example 2:-
Take the limit of the f(x) as x approaches 𝑖
𝑓 𝑥 =
𝑥2 + 1
𝑥 − 𝑖
lim
𝑥→𝑖
𝑓 𝑥 = 2𝑖
f(0.9𝒊) f(0.99𝒊) f(0.999𝒊) f(𝒊) f(1.001𝒊) f(1.01𝒊) f(1.1𝒊)
1.900𝒊 1.990𝒊 1.999𝒊 undefine
d
2.001𝒊 2.010𝒊 2.100𝒊
As x approaches 𝑖 from both sides f(x) gets closer and closer to 2𝑖, therefore
making 2𝑖 the limit of f(x) as x approaches 𝑖. The limit still exists even
though f(𝑖) does not exist because as x draws closer to 𝑖 f(x) draws closer to
2𝑖 making it the limit to the function.

10. CivilEngineering
 Many aspects of civil engineering require calculus. Firstly, derivation of the
basic fluid mechanics equations requires limits. For example, all hydraulic
analysis programs, which aid in the design of storm drain and open channel
systems, use calculus numerical methods to obtain the results.
Some applications of limit:-

11. Mechanical Engineering
 In mechanical engineering, limit is used for computing the surface area of
complex objects to determine frictional forces, designing a pump according
to flow rate and head, and calculating the power provided by a battery
system

12. Aerospace Engineering
 Analysis of rockets that function in stages require calculus, as does
gravitational modeling over time and space. Almost all physics models,
especially those of astronomy and complex systems, use some form of
limits.

13. The reading of your speedometer (e.g., 85 km/h) is a limit in the real world. Your
speed is changing continuously during time.

14. Business
 In business, limits can help us by providing an
accurate and measurable way to record changes
in variables using numbers and mathematics.
 Derivatives in calculus can be used to
determine maximum profit, minimum cost,
rate of change of cost, and how to maximize/
minimize profit, cost or production.

15. Medicine
 By using the principles of calculus, we can find how fast a tumor is
shrinking/growing, the size when the tumor will stop growing and
when certain treatments should be given and finding the volume of
a tumor.
 Calculus can be used to determine the blood flow in an artery or a
vein at a given point in time.
 Calculus can be used to find the amount of blood pumped through
the heart per unit time.
 In biology, it is utilized to formulate rates such as birth and death
rates.

16. • To a machinist manufacturing a piston, close may mean within a few
thousandths of an inch.
• To an astronomer studying distant galaxies, close may mean within a few
thousand light-years.
Thank you