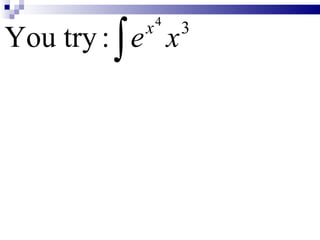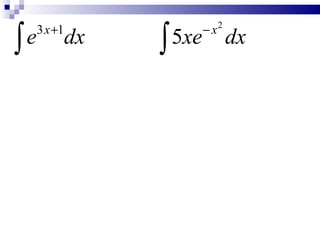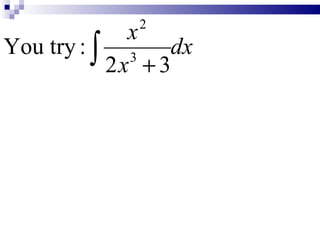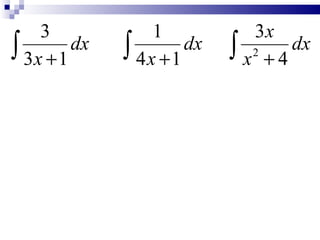1) The document discusses integration as the reverse process of differentiation, and provides examples of integrating logarithmic and exponential functions. 2) Key points covered include integrating 1/x as ln(x), and exponential functions like e3x by using u-substitution and dividing the "tail" by the exponent. 3) The document also demonstrates integrating logarithmic expressions using u-substitution, letting the term in the denominator equal u and finding du.

1. 5.3 Integration of
Logarithmic and
Exponential Functions

2. 1
We recall that the derivative of ln x is .
x
1
So if we go in reverse, then ∫ dx = ln x .
x
(Absolute values are necessary.)
CAREFUL!Don' t get this confused with the ones you
you have done like this one :
1 x −1 −1
∫ x 2 dx = ∫ x dx = − 1 + C = x + C
−2

3. 3
∫ 2v dv
∫t
−1
dt

4. ∫(x )dx
−1 −2
3
+x −x +x 2
∫ ( 4e )dt
−1
0 .5 t
+ 2t

5. ( )
You try : ∫ x 2 − x + x −1 − x −3 dx
∫ ( 4e )
−1
0.4 x
+ 7 x dx

6. Figuring out how to undo the
derivative of exponentials
x x
You remember that the derivative of e is e .
So if you go in reverse, ∫ e x dx will be e x + C.
If only they were all that simple.
We need to consider what happens when they
3x
were a little fancier like e .

7. The derivative of e would be e ⋅ 3 = 3e .
3x 3x 3x
So it appears that in order to go in reverse,
the opposite of multiplying by the " tail, "
maybe we will divide by it. Let' s try it :
3x
3e
∫ 3e dx = 3 + C = e + C
3x 3x

8. ∫e
7x
dx
∫ e − x / 4 dx
∫ e.04 x dx

9. We can use u-substitution
with the exponentials
∫ e du = e + C
u u

10. Using ∫ e du = e + C
u u
∫e
x3 2
x dx It is obvious what u should be!
u=x 3
du = 3x dx 2

11. You try : ∫ e x
4
x 3

12. ∫ ∫
3 x +1 − x2
e dx 5xe dx

13. We can use u-substitution with
the logarithmic types too
1
∫u du = ln u + C

14. 1
Using ∫ du = ln u + C
u
x3
∫ x 4 + 1 dx Let's call the stuff in the denominator u.
u = x +1
4
du = 4 x 3 dx
1
∫ x4 + 1 x 3 dx =

15. 2
x
You try : ∫ 3 dx
2x + 3

16. 3 1 3x
∫ 3x + 1 dx ∫ 4x +1 dx ∫ x2 + 4 dx