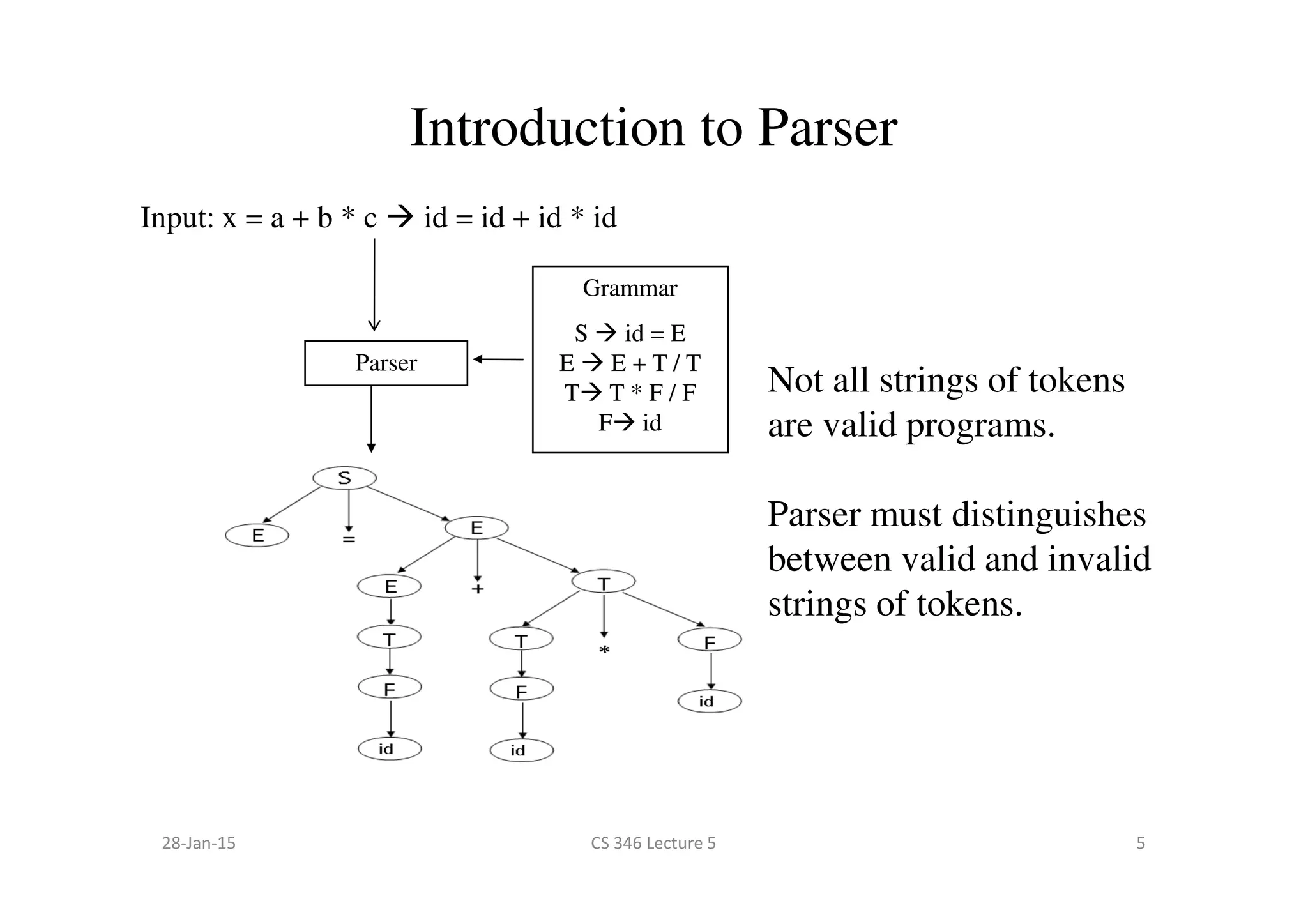
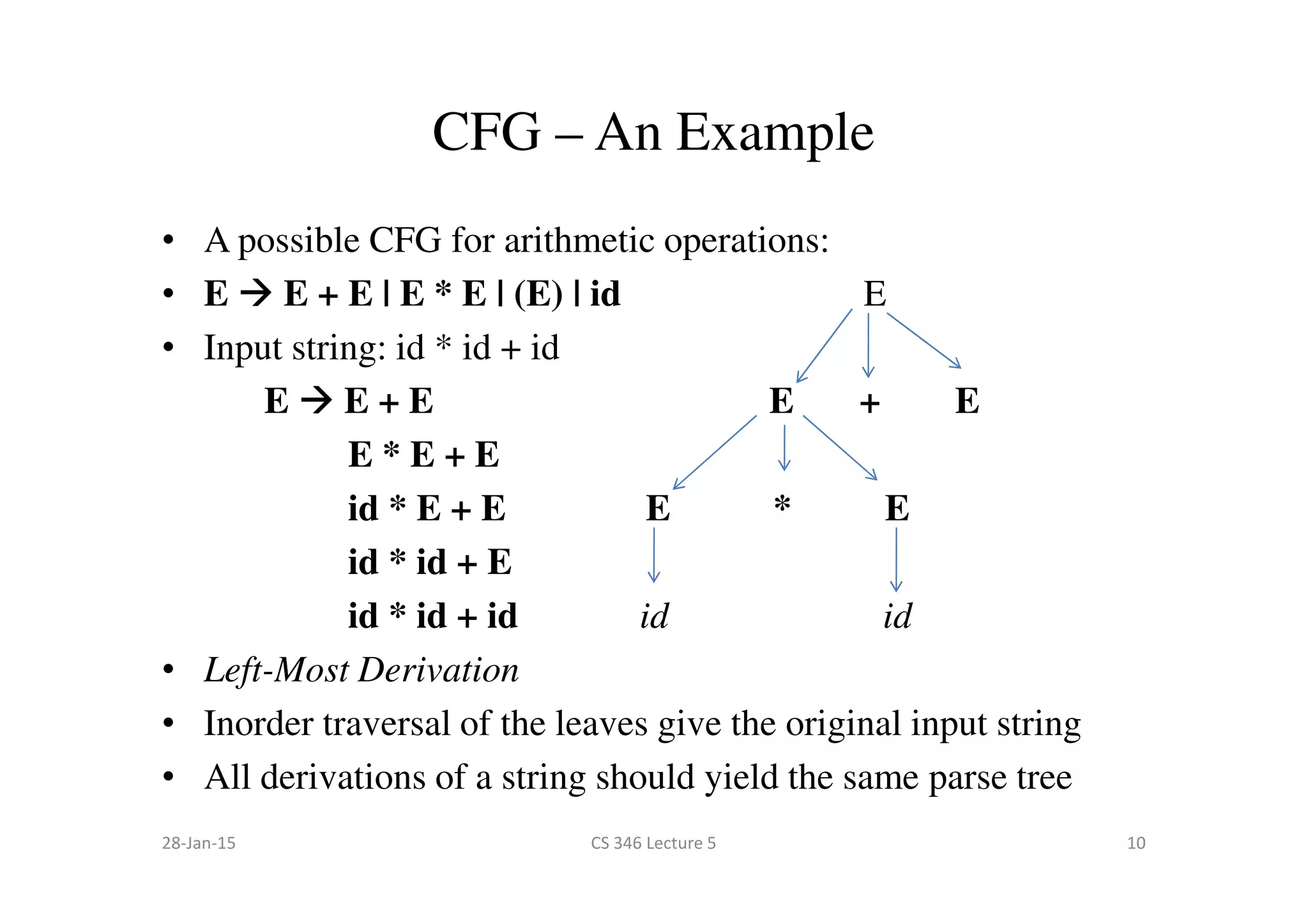
This document discusses context-free grammars and parsing. It introduces regular languages and their limitations, such as not being able to express balanced parentheses. A context-free grammar is then presented as a formal way to describe the valid strings of a language using terminals, non-terminals, productions, and a start symbol. An example grammar for balanced parentheses is given. The role of a parser to take tokens as input and output a parse tree or syntax error based on a grammar is described.

1. Syntax Analysis I
Lecture 5
Introduction to Parsing

2. Regular Languages
• Weakest formal languages widely used
• Many applications
– Lexical Analysis
• Some languages are not regular
• Consider the language
{( i ) i | i ≥ 0}
28-Jan-15 2CS 346 Lecture 5

3. Limitation of Regular Expression
• RE can’t express balance of the nested
parenthesis
• Also can’t express nested loop structure
• What can regular languages express?• What can regular languages express?
S0 S1
1
1
00 • RE can count mod k
• But RE can’t count a number
28-Jan-15 3CS 346 Lecture 5

4. Introduction to Parser
• What the parser do?
– Input to the parser: Sequence of tokens from lexer
– Output of the parser: parse tree of the program
Parser
Input
Grammar
Output or Syntax error
28-Jan-15 4CS 346 Lecture 5

5. Parser
Input: x = a + b * c id = id + id * id
Grammar
S id = E
E E + T / T
T T * F / F
F id
Introduction to Parser
Not all strings of tokens
are valid programs.
Parser must distinguishes
between valid and invalid
strings of tokens.
28-Jan-15 5CS 346 Lecture 5

6. Requirements
• A language is needed for describing valid
strings of tokens
• A method for distinguishing valid strings from• A method for distinguishing valid strings from
the invalid strings
• Programming languages have natural recursive
structure
– if (expr) expr else expr
28-Jan-15 6CS 346 Lecture 5

7. Context Free Grammar
• Formally a CFG G = (T, N, S, P), where:
– T is the set of terminal symbols in the grammar (i.e., the set of
tokens returned by the lexical analyzer)
– N, the non-terminals, are variables that denote sets of
(sub)strings occurring in the language. These impose a structure
on the grammar.
(sub)strings occurring in the language. These impose a structure
on the grammar.
– S is the goal symbol, a distinguished non-terminal in N denoting
the entire set of strings in L(G).
– P is a finite set of productions specifying how terminals and non-
terminals can be combined to form strings in the language. Each
production must have a single non-terminal on its left hand side.
28-Jan-15 7CS 346 Lecture 5

8. CFG – An Example
• Production : X Y1… … YN where
X ϵ N and Yi ϵ N U T U {ɛ}
• The language for balanced parenthesis, i.e.
{( i ) i | i ≥ 0}, CFG productions are{( ) | i ≥ 0}, CFG productions are
S (S)|S
S ɛ
where set of non-Terminals (N) = {S}, set of
Terminals (T)= {(, )} and S is the start symbol
28-Jan-15 8CS 346 Lecture 5

9. Productions represents some rules
• Begin with a string with only the start symbol S
• Replace non terminal X in the string by the RHS of
the some production
– Let X Y … … Y and there is a string– Let X Y1… … Yn and there is a string
– x1… … xi X xi+1… … xN; after using above production
rule, it can be written as
– x1… … xi Y1… … Yn xi+1… … xN
• If α0 α1 α2 … … αn α0 αn
28-Jan-15 9CS 346 Lecture 5

10. • A possible CFG for arithmetic operations:
• E E + E | E * E | (E) | id E
• Input string: id * id + id
E E + E E + E
E * E + E
CFG – An Example
E * E + E
id * E + E E * E
id * id + E
id * id + id id id
• Left-Most Derivation
• Inorder traversal of the leaves give the original input string
• All derivations of a string should yield the same parse tree
28-Jan-15 10CS 346 Lecture 5