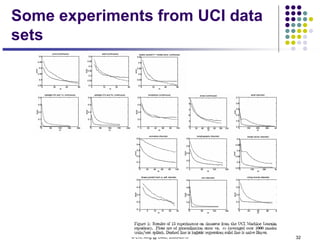
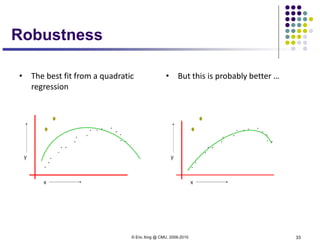
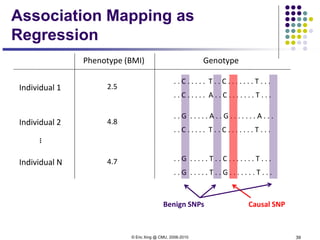
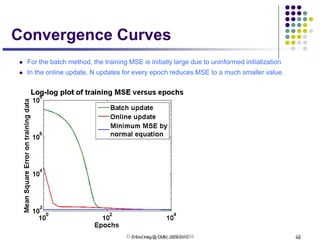
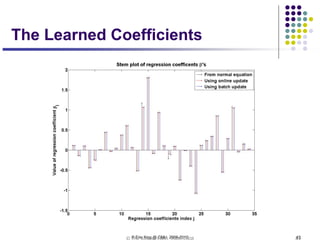
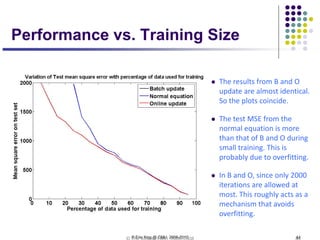
This document discusses generative and discriminative classifiers. Generative classifiers model the joint distribution of data and labels, while discriminative classifiers directly model the conditional probability of labels given data. Naive Bayes is an example of a generative classifier, while logistic regression is a discriminative classifier that directly models the probability of a label given input features. The document provides mathematical details on naive Bayes, logistic regression, and how logistic regression can be trained to maximize conditional likelihood through gradient descent.

1. © Eric Xing @ CMU, 2006-2010 1
Machine Learning
Generative verses discriminative
classifier
Eric Xing
Lecture 2, August 12, 2010
Reading:

2. © Eric Xing @ CMU, 2006-2010 2
Generative and Discriminative
classifiers
 Goal: Wish to learn f: X → Y, e.g., P(Y|X)
 Generative:
 Modeling the joint distribution
of all data
 Discriminative:
 Modeling only points
at the boundary

3. © Eric Xing @ CMU, 2006-2010 3
Generative vs. Discriminative
Classifiers
 Goal: Wish to learn f: X → Y, e.g., P(Y|X)
 Generative classifiers (e.g., Naïve Bayes):
 Assume some functional form for P(X|Y), P(Y)
This is a ‘generative’ model of the data!
 Estimate parameters of P(X|Y), P(Y) directly from training data
 Use Bayes rule to calculate P(Y|X= x)
 Discriminative classifiers (e.g., logistic regression)
 Directly assume some functional form for P(Y|X)
This is a ‘discriminative’ model of the data!
 Estimate parameters of P(Y|X) directly from training data
Yn
Xn
Yn
Xn

4. © Eric Xing @ CMU, 2006-2010 4
Suppose you know the following
…
 Class-specific Dist.: P(X|Y)
 Class prior (i.e., "weight"): P(Y)
 This is a generative model of the data!
),;(
)|(
111
1
Σ=
=
µ

Xp
YXp
),;(
)|(
222
2
Σ=
=
µ

Xp
YXp
Bayes classifier:

5. © Eric Xing @ CMU, 2006-2010 5
Optimal classification
 Theorem: Bayes classifier is optimal!
 That is
 How to learn a Bayes classifier?
 Recall density estimation. We need to estimate P(X|y=k), and P(y=k) for all k

6. © Eric Xing @ CMU, 2006-2010 6
Gaussian Discriminative Analysis
 learning f: X → Y, where
 X is a vector of real-valued features, Xn= < Xn,1…Xn,m >
 Y is an indicator vector
 What does that imply about the form of P(Y|X)?
 The joint probability of a datum and its label is:
 Given a datum xn, we predict its label using the conditional probability of the label
given the datum:
Yn
Xn
{ }2
2
1
2/12
)-(-exp
)2(
1
),,1|()1(),|1,(
2 knk
k
nn
k
n
k
nn ypypyp
µ
πσ
π
σµσµ
σ
x
xx
=
=×===
{ }
{ }∑ −−
−−
==
'
2
'2
1
2/12'
2
2
1
2/12
)(exp
)2(
1
)(exp
)2(
1
),,|1(
2
2
k
knk
knk
n
k
nyp
µ
πσ
π
µ
πσ
π
σµ
σ
σ
x
x
x

7. © Eric Xing @ CMU, 2006-2010 7
Conditional Independence
 X is conditionally independent of Y given Z, if the probability
distribution governing X is independent of the value of Y, given
the value of Z
Which we often write
 e.g.,
 Equivalent to:

8. © Eric Xing @ CMU, 2006-2010 8
Naïve Bayes Classifier
 When X is multivariate-Gaussian vector:
 The joint probability of a datum and it label is:
 The naïve Bayes simplification
 More generally:
 Where p(. | .) is an arbitrary conditional (discrete or continuous) 1-D density
{ })-()-(-exp
)2(
1
),,1|()1(),|1,(
1
2
1
2/1 kn
T
knk
k
nn
k
n
k
nn ypypyp
µµ
π
π
µµ


xx
xx
−
Σ
Σ
=
Σ=×==Σ=
Yn
Xn
{ }∏
∏
=
=×===
j
jkjn
jk
k
j
jkjk
k
njn
k
n
k
nn
x
yxpypyp
jk
2
,,2
1
2/12
,
,,,
)-(-exp
)2(
1
),,1|()1(),|1,(
2
,
µ
πσ
π
σµσµ
σ
x
∏=
×=
m
j
njnnnn yxpypyp
1
, ),|()|(),|,( ηππηx
Yn
Xn,1 Xn,2 Xn,m
…

9. © Eric Xing @ CMU, 2006-2010 9
The predictive distribution
 Understanding the predictive distribution
 Under naïve Bayes assumption:
 For two class (i.e., K=2), and when the two classes haves the same
variance, ** turns out to be a logistic function
*
),|,(
),|,(
),|(
),,|,(
),,,|(
' '''∑ Σ
Σ
=
Σ
Σ=
=Σ=
k kknk
kknk
n
n
k
n
n
k
n
xN
xN
xp
xyp
xyp
µπ
µπ
µ
πµ
πµ 

 1
1
( ){ }1
1
222
122
1
1
2
222
1
2
12
21
1
21
1
1
1
1
1
π
π
σσσµπ
σµπ
µµµµ
σ
σ
)(2
log)-(exp
log)-(exp
log)][-]([)-(exp −
















−−−
















−−−
++−+
=
∑
∑
+
=
∑j
jjjjj
nCx
Cx
jj
j j
jj
n
j
j j
jj
n
j
x
n
T
x
e θ−
+
=
1
1
)|( nn xyp 11
=
**
log)(exp
log)(exp
),,,|(
' ,''
,'
'
,
,
∑ ∑
∑
















−−−−
















−−−−
=Σ=
k j jk
j
k
j
n
jk
k
j jk
j
k
j
n
jk
k
n
k
n
Cx
Cx
xyp
σµ
σ
π
σµ
σ
π
πµ
2
2
2
2
2
1
2
1
1


10. © Eric Xing @ CMU, 2006-2010 10
The decision boundary
 The predictive distribution
 The Bayes decision rule:
 For multiple class (i.e., K>2), * correspond to a softmax function
∑
−
−
==
j
x
x
n
k
n
n
T
j
n
T
k
e
e
xyp θ
θ
)|( 1
n
T
xM
j
j
nj
nn
e
x
xyp θ
θθ
−
=
+
=






−−+
==
∑
1
1
1
1
1
0
1
1
exp
)|(
n
T
x
x
x
nn
nn
x
e
e
e
xyp
xyp
n
T
n
T
n
T
θ
θ
θ
θ
=












+
+=
=
=
−
−
−
1
1
1
1
1
2
1
ln
)|(
)|(
ln

11. © Eric Xing @ CMU, 2006-2010 11
Generative vs. Discriminative
Classifiers
 Goal: Wish to learn f: X → Y, e.g., P(Y|X)
 Generative classifiers (e.g., Naïve Bayes):
 Assume some functional form for P(X|Y), P(Y)
This is a ‘generative’ model of the data!
 Estimate parameters of P(X|Y), P(Y) directly from training data
 Use Bayes rule to calculate P(Y|X= x)
 Discriminative classifiers:
 Directly assume some functional form for P(Y|X)
This is a ‘discriminative’ model of the data!
 Estimate parameters of P(Y|X) directly from training data
Yi
Xi
Yi
Xi

12. © Eric Xing @ CMU, 2006-2010 12
Linear Regression
 The data:
 Both nodes are observed:
 X is an input vector
 Y is a response vector
(we first consider y as a generic
continuous response vector, then
we consider the special case of
classification where y is a discrete
indicator)
 A regression scheme can be
used to model p(y|x) directly,
rather than p(x,y)
Yi
Xi
N
{ }),(,),,(),,(),,( NN yxyxyxyx 332211

13. © Eric Xing @ CMU, 2006-2010 13
Linear Regression
 Assume that Y (target) is a linear function of X (features):
 e.g.:
 let's assume a vacuous "feature" X0=1 (this is the intercept term, why?), and
define the feature vector to be:
 then we have the following general representation of the linear function:
 Our goal is to pick the optimal . How!
 We seek that minimize the following cost function:
θ
θ
∑=
−=
n
i
iii yxyJ
1
2
2
1
))(ˆ()(

θ

14. © Eric Xing @ CMU, 2006-2010 14
The Least-Mean-Square (LMS)
method
 Consider a gradient descent algorithm:
 Now we have the following descent rule:
 For a single training point, we have:
 This is known as the LMS update rule, or the Widrow-Hoff learning rule
 This is actually a "stochastic", "coordinate" descent algorithm
 This can be used as a on-line algorithm
∑=
+
−+=
n
i
j
i
tT
ii
t
j
t
j xy
1
1
)( θαθθ x

j
i
tT
ii
t
j
t
j xy )(
1
θαθθ x

−+=
+
tj
t
j
t
j J )(θ
θ
αθθ
∂
∂
−=
+1

15. © Eric Xing @ CMU, 2006-2010 15
Probabilistic Interpretation of
LMS
 Let us assume that the target variable and the inputs are
related by the equation:
where ε is an error term of unmodeled effects or random noise
 Now assume that ε follows a Gaussian N(0,σ), then we have:
 By independence assumption:
ii
T
iy εθ += x





 −
−= 2
2
22
1
σ
θ
σπ
θ
)(
exp);|( i
T
i
ii
y
xyp
x







 −
−





==
∑
∏ =
=
2
1
2
1 22
1
σ
θ
σπ
θθ
n
i i
T
i
nn
i
ii
y
xypL
)(
exp);|()(
x

16. © Eric Xing @ CMU, 2006-2010 16
Probabilistic Interpretation of
LMS, cont.
 Hence the log-likelihood is:
 Do you recognize the last term?
Yes it is:
 Thus under independence assumption, LMS is equivalent to
MLE of θ !
∑=
−−=
n
i i
T
iynl 1
2
2
2
11
2
1
)(log)( xθ
σσπ
θ
∑=
−=
n
i
i
T
i yJ
1
2
2
1
)()( θθ x

17. © Eric Xing @ CMU, 2006-2010 17
Classification and logistic
regression

18. © Eric Xing @ CMU, 2006-2010 18
The logistic function

19. © Eric Xing @ CMU, 2006-2010 19
Logistic regression (sigmoid
classifier)
 The condition distribution: a Bernoulli
where µ is a logistic function
 We can used the brute-force gradient method as in LR
 But we can also apply generic laws by observing the p(y|x) is
an exponential family function, more specifically, a
generalized linear model (see future lectures …)
yy
xxxyp −
−= 1
1 ))(()()|( µµ
xT
e
x θ
µ −
+
=
1
1
)(

20. © Eric Xing @ CMU, 2006-2010 20
Training Logistic Regression:
MCLE
 Estimate parameters θ=<θ0, θ1, ... θm> to maximize the
conditional likelihood of training data
 Training data
 Data likelihood =
 Data conditional likelihood =

21. © Eric Xing @ CMU, 2006-2010 21
Expressing Conditional Log
Likelihood
 Recall the logistic function:
and conditional likelihood:

22. © Eric Xing @ CMU, 2006-2010 22
Maximizing Conditional Log
Likelihood
 The objective:
 Good news: l(θ) is concave function of θ
 Bad news: no closed-form solution to maximize l(θ)

23. © Eric Xing @ CMU, 2006-2010 23
The Newton’s method
 Finding a zero of a function

24. © Eric Xing @ CMU, 2006-2010 24
The Newton’s method (con’d)
 To maximize the conditional likelihood l(θ):
since l is convex, we need to find θ∗ where l’(θ∗)=0 !
 So we can perform the following iteration:

25. © Eric Xing @ CMU, 2006-2010 25
The Newton-Raphson method
 In LR the θ is vector-valued, thus we need the following
generalization:
 ∇ is the gradient operator over the function
 H is known as the Hessian of the function

26. © Eric Xing @ CMU, 2006-2010 26
The Newton-Raphson method
 In LR the θ is vector-valued, thus we need the following
generalization:
 ∇ is the gradient operator over the function
 H is known as the Hessian of the function

27. © Eric Xing @ CMU, 2006-2010 27
Iterative reweighed least squares
(IRLS)
 Recall in the least square est. in linear regression, we have:
which can also derived from Newton-Raphson
 Now for logistic regression:

28. © Eric Xing @ CMU, 2006-2010 28
Generative vs. Discriminative
Classifiers
 Goal: Wish to learn f: X → Y, e.g., P(Y|X)
 Generative classifiers (e.g., Naïve Bayes):
 Assume some functional form for P(X|Y), P(Y)
This is a ‘generative’ model of the data!
 Estimate parameters of P(X|Y), P(Y) directly from training data
 Use Bayes rule to calculate P(Y|X= x)
 Discriminative classifiers:
 Directly assume some functional form for P(Y|X)
This is a ‘discriminative’ model of the data!
 Estimate parameters of P(Y|X) directly from training data
Yi
Xi
Yi
Xi

29. © Eric Xing @ CMU, 2006-2010 29
Naïve Bayes vs Logistic
Regression
 Consider Y boolean, X continuous, X=<X1 ... Xm>
 Number of parameters to estimate:
NB:
LR:
 Estimation method:
 NB parameter estimates are uncoupled
 LR parameter estimates are coupled
**
log)(
2
1
exp
log)(
2
1
exp
)|(
' ,'
2
,'2
,'
'
,
2
,2
,
∑ ∑
∑
















−−−−
















−−−−
=
k j jkjkj
jk
k
j jkjkj
jk
k
Cx
Cx
yp
σµ
σ
π
σµ
σ
π
x
xT
e
x θ
µ −
+
=
1
1
)(

30. © Eric Xing @ CMU, 2006-2010 30
Naïve Bayes vs Logistic
Regression
 Asymptotic comparison (# training examples → infinity)
 when model assumptions correct
 NB, LR produce identical classifiers
 when model assumptions incorrect
 LR is less biased – does not assume conditional independence
 therefore expected to outperform NB

31. © Eric Xing @ CMU, 2006-2010 31
Naïve Bayes vs Logistic
Regression
 Non-asymptotic analysis (see [Ng & Jordan, 2002] )
 convergence rate of parameter estimates – how many training
examples needed to assure good estimates?
NB order log m (where m = # of attributes in X)
LR order m
 NB converges more quickly to its (perhaps less helpful)
asymptotic estimates

32. © Eric Xing @ CMU, 2006-2010 32
Some experiments from UCI data
sets

33. © Eric Xing @ CMU, 2006-2010 33
Robustness
• The best fit from a quadratic
regression
• But this is probably better …

34. © Eric Xing @ CMU, 2006-2010 34
Bayesian Parameter Estimation
 Treat the distribution parameters θ also as a random variable
 The a posteriori distribution of θ after seem the data is:
This is Bayes Rule
likelihoodmarginal
priorlikelihood
posterior
×
=
∫
==
θθθ
θθθθ
θ
dpDp
pDp
Dp
pDp
Dp
)()|(
)()|(
)(
)()|(
)|(
The prior p(.) encodes our prior knowledge about the domain

35. © Eric Xing @ CMU, 2006-2010 35
35
What if is not invertible ?
log likelihood log prior
Prior belief that β is Gaussian with zero-mean biases solution to “small” β
I) Gaussian Prior
0
Ridge Regression
Closed form: HW
Regularized Least Squares and
MAP

36. © Eric Xing @ CMU, 2006-2010 36
Regularized Least Squares and
MAP
36
What if is not invertible ?
log likelihood log prior
Prior belief that β is Laplace with zero-mean biases solution to “small” β
Lasso
Closed form: HW
II) Laplace Prior

37. © Eric Xing @ CMU, 2006-2010 37
Ridge Regression vs Lasso
37
Ridge Regression: Lasso: HOT
!
Lasso (l1 penalty) results in sparse solutions – vector with more zero coordinates
Good for high-dimensional problems – don’t have to store all coordinates!
βs with
constant
l1 norm
βs with constant J(β)
(level sets of J(β))
βs with
constant
l2 norm
β2
β1

38. © Eric Xing @ CMU, 2006-2010 38
Case study:
predicting gene expression
The genetic picture
CGTTTCACTGTACAATTT
causal SNPs
a univariate phenotype:
i.e., the expression intensity of
a gene

39. © Eric Xing @ CMU, 2006-2010 39
Individual 1
Individual 2
Individual N
Phenotype (BMI)
2.5
4.8
4.7
Genotype
. . C . . . . . T . . C . . . . . . . T . . .
. . C . . . . . A . . C . . . . . . . T . . .
. . G . . . . . A . . G . . . . . . . A . . .
. . C . . . . . T . . C . . . . . . . T . . .
. . G . . . . . T . . C . . . . . . . T . . .
. . G . . . . . T . . G . . . . . . . T . . .
Causal SNPBenign SNPs
…
Association Mapping as
Regression

40. © Eric Xing @ CMU, 2006-2010 40
Individual 1
Individual 2
Individual N
Phenotype (BMI)
2.5
4.8
4.7
Genotype
. . 0 . . . . . 1 . . 0 . . . . . . . 0 . . .
. . 1 . . . . . 1 . . 1 . . . . . . . 1 . . .
. . 2 . . . . . 2 . . 1 . . . . . . . 0 . . .
…
yi = ∑=
J
j
jijx
1
β SNPs with large
|βj| are relevant
Association Mapping as
Regression

41. © Eric Xing @ CMU, 2006-2010 41
Experimental setup
 Asthama dataset
 543 individuals, genotyped at 34 SNPs
 Diploid data was transformed into 0/1 (for homozygotes) or 2 (for heterozygotes)
 X=543x34 matrix
 Y=Phenotype variable (continuous)
 A single phenotype was used for regression
 Implementation details
 Iterative methods: Batch update and online update implemented.
 For both methods, step size α is chosen to be a small fixed value (10-6). This
choice is based on the data used for experiments.
 Both methods are only run to a maximum of 2000 epochs or until the change in
training MSE is less than 10-4

42. © Eric Xing @ CMU, 2006-2010 42© Eric Xing @ CMU, 2006-2008 42
 For the batch method, the training MSE is initially large due to uninformed initialization
 In the online update, N updates for every epoch reduces MSE to a much smaller value.
Convergence Curves

43. © Eric Xing @ CMU, 2006-2010 43
The Learned Coefficients

44. © Eric Xing @ CMU, 2006-2010 44
 The results from B and O
update are almost identical.
So the plots coincide.
 The test MSE from the
normal equation is more
than that of B and O during
small training. This is
probably due to overfitting.
 In B and O, since only 2000
iterations are allowed at
most. This roughly acts as a
mechanism that avoids
overfitting.
Performance vs. Training Size

45. © Eric Xing @ CMU, 2006-2010 45
Summary
 Naïve Bayes classifier
 What’s the assumption
 Why we use it
 How do we learn it
 Logistic regression
 Functional form follows from Naïve Bayes assumptions
 For Gaussian Naïve Bayes assuming variance
 For discrete-valued Naïve Bayes too
 But training procedure picks parameters without the conditional independence
assumption
 Gradient ascent/descent
 – General approach when closed-form solutions unavailable
 Generative vs. Discriminative classifiers
 – Bias vs. variance tradeoff

46. © Eric Xing @ CMU, 2006-2010 46
Appendix

47. © Eric Xing @ CMU, 2006-2010 47
Parameter Learning from iid Data
 Goal: estimate distribution parameters θ from a dataset of N
independent, identically distributed (iid), fully observed,
training cases
D = {x1, . . . , xN}
 Maximum likelihood estimation (MLE)
1. One of the most common estimators
2. With iid and full-observability assumption, write L(θ) as the likelihood of the data:
3. pick the setting of parameters most likely to have generated the data we saw:
);,,()( , θθ NxxxPL 21=
∏=
=
=
N
i i
N
xP
xPxPxP
1
2
);(
);(,),;();(
θ
θθθ 
)(maxarg*
θθ
θ
L= )(logmaxarg θ
θ
L=

48. © Eric Xing @ CMU, 2006-2010 48
Example: Bernoulli model
 Data:
 We observed N iid coin tossing: D={1, 0, 1, …, 0}
 Representation:
Binary r.v:
 Model:
 How to write the likelihood of a single observation xi ?
 The likelihood of datasetD={x1, …,xN}:
ii xx
ixP −
−= 1
1 )()( θθ
( )∏∏ =
−
=
−==
N
i
xx
N
i
iN
ii
xPxxxP
1
1
1
21 1 )()|()|,...,,( θθθθ
},{ 10=nx
tails#head#
)()( θθθθ −=
∑
−
∑
= ==
−
11 11
1
N
i
i
N
i
i xx



=
=−
=
1
01
x
x
xP
for
for
)(
θ
θ xx
xP −
−= 1
1 )()( θθ⇒

49. © Eric Xing @ CMU, 2006-2010 49
Maximum Likelihood Estimation
 Objective function:
 We need to maximize this w.r.t. θ
 Take derivatives wrt θ
 Sufficient statistics
 The counts, are sufficient statistics of data D
)log()(log)(log)|(log);( θθθθθθ −−+=−== 11 hh
nn
nNnDPD th
l
0
1
=
−
−
−=
∂
∂
θθθ
hh nNnl
N
nh
MLE =θ

∑=
i
iMLE x
N
1
θ

or
Frequency as
sample mean
,where, ∑= i ikh xnn

50. © Eric Xing @ CMU, 2006-2010 50
Overfitting
 Recall that for Bernoulli Distribution, we have
 What if we tossed too few times so that we saw zero head?
We have and we will predict that the probability of
seeing a head next is zero!!!
 The rescue: "smoothing"
 Where n' is know as the pseudo- (imaginary) count
 But can we make this more formal?
tailhead
head
head
ML
nn
n
+
=θ

,0=head
MLθ

'
'
nnn
nn
tailhead
head
head
ML
++
+
=θ


51. © Eric Xing @ CMU, 2006-2010 51
Bayesian Parameter Estimation
 Treat the distribution parameters θ also as a random variable
 The a posteriori distribution of θ after seem the data is:
This is Bayes Rule
likelihoodmarginal
priorlikelihood
posterior
×
=
∫
==
θθθ
θθθθ
θ
dpDp
pDp
Dp
pDp
Dp
)()|(
)()|(
)(
)()|(
)|(
The prior p(.) encodes our prior knowledge about the domain

52. © Eric Xing @ CMU, 2006-2010 52
Frequentist Parameter Estimation
Two people with different priors p(θ) will end up with
different estimates p(θ|D).
 Frequentists dislike this “subjectivity”.
 Frequentists think of the parameter as a fixed, unknown
constant, not a random variable.
 Hence they have to come up with different "objective"
estimators (ways of computing from data), instead of using
Bayes’ rule.
 These estimators have different properties, such as being “unbiased”, “minimum
variance”, etc.
 The maximum likelihood estimator, is one such estimator.

53. © Eric Xing @ CMU, 2006-2010 53
Discussion
θ or p(θ), this is the problem!
Bayesians know it

54. © Eric Xing @ CMU, 2006-2010 54
Bayesian estimation for Bernoulli
 Beta distribution:
 When x is discrete
 Posterior distribution of θ :
 Notice the isomorphism of the posterior to the prior,
 such a prior is called a conjugate prior
 α and β are hyperparameters (parameters of the prior) and correspond to the
number of “virtual” heads/tails (pseudo counts)
1111
1
1
1 111 −+−+−−
−=−×−∝= βαβα
θθθθθθ
θθ
θ thth nnnn
N
N
N
xxp
pxxp
xxP )()()(
),...,(
)()|,...,(
),...,|(
1111
11 −−−−
−=−
ΓΓ
+Γ
= βαβα
θθβαθθ
βα
βα
βαθ )(),()(
)()(
)(
),;( BP
!)()( xxxx =Γ=+Γ 1

55. © Eric Xing @ CMU, 2006-2010 55
Bayesian estimation for
Bernoulli, con'd
 Posterior distribution of θ :
 Maximum a posteriori (MAP) estimation:
 Posterior mean estimation:
 Prior strength: A=α+β
 A can be interoperated as the size of an imaginary data set from which we obtain
the pseudo-counts
1111
1
1
1 111 −+−+−−
−=−×−∝= βαβα
θθθθθθ
θθ
θ thth nnnn
N
N
N
xxp
pxxp
xxP )()()(
),...,(
)()|,...,(
),...,|(
∫ ∫ ++
+
=−×== −+−+
βα
α
θθθθθθθθ βα
N
n
dCdDp hnn
Bayes
th 11
1 )()|(
Bata parameters
can be understood
as pseudo-counts
),...,|(logmaxarg NMAP xxP 1θθ
θ
=

56. © Eric Xing @ CMU, 2006-2010 56
Effect of Prior Strength
 Suppose we have a uniform prior (α=β=1/2),
and we observe
 Weak prior A = 2. Posterior prediction:
 Strong prior A = 20. Posterior prediction:
 However, if we have enough data, it washes away the prior.
e.g., . Then the estimates under
weak and strong prior are and , respectively,
both of which are close to 0.2
),( 82 === th nnn

250
102
21
282 .)',,|( =
+
+
=×==== αα

th nnhxp
400
1020
210
2082 .)',,|( =
+
+
=×==== αα

th nnhxp
),( 800200 === th nnn

10002
2001
+
+
100020
20010
+
+

57. © Eric Xing @ CMU, 2006-2010 57
Example 2: Gaussian density
 Data:
 We observed N iid real samples:
D={-0.1, 10, 1, -5.2, …, 3}
 Model:
 Log likelihood:
 MLE: take derivative and set to zero:
( ) { }22212
22 σµπσ /)(exp)(
/
−−=
−
xxP
( )
∑=
−
−−==
N
n
nxN
DPD
1
2
2
2
2
1
2
2 σ
µ
πσθθ )log()|(log);(l
( )
( )∑
∑
−+−=
∂
∂
−=
∂
∂
n n
n n
x
N
x
2
422
2
2
1
2
1
µ
σσσ
µσ
µ
l
l
)/( ( )
( )∑
∑
−=
=
n MLnMLE
n nMLE
x
N
x
N
22 1
1
µσ
µ

58. © Eric Xing @ CMU, 2006-2010 58
MLE for a multivariate-Gaussian
 It can be shown that the MLE for µ and Σ is
where the scatter matrix is
 The sufficient statistics are Σnxn and Σnxnxn
T.
 Note that XTX=Σnxnxn
T may not be full rank (eg. if N <D), in which case ΣML is not
invertible
( )
( )( ) S
N
xx
N
x
N
n
T
MLnMLnMLE
n nMLE
11
1
=−−=Σ
=
∑
∑
µµ
µ
( )( ) ( ) T
MLMLn n
T
nnn
T
MLnMLn NxxxxS µµµµ −=−−= ∑∑














=
K
n
n
n
n
x
x
x
x

2
1














−−−−−−
−−−−−−
−−−−−−
=
T
N
T
T
x
x
x
X

2
1

59. © Eric Xing @ CMU, 2006-2010 59
Bayesian estimation
 Normal Prior:
 Joint probability:
 Posterior:
( ) { }2
0
2
0
212
0 22 σµµπσµ /)(exp)(
/
−−=
−
P
1
2
0
2
2
02
0
2
2
0
2
0
2
2
1
1
1
1
−






+=
+
+
+
=
σσ
σµ
σσ
σ
σσ
σ
µ
N
N
x
N
N ~and,
//
/
//
/~where
Sample mean
( ) ( )
( ) { }2
0
2
0
212
0
1
2
2
22
22
2
1
2
σµµπσ
µ
σ
πσµ
/)(exp
exp),(
/
/
−−×






−−=
−
=
−
∑
N
n
n
N
xxP
( ) { }22212
22 σµµσπµ ~/)~(exp~)|(
/
−−=
−
xP

60. © Eric Xing @ CMU, 2006-2010 60
Bayesian estimation: unknown µ, known σ
 The posterior mean is a convex combination of the prior and the MLE, with
weights proportional to the relative noise levels.
 The precision of the posterior 1/σ2
N is the precision of the prior 1/σ2
0 plus one
contribution of data precision 1/σ2 for each observed data point.
 Sequentially updating the mean
 µ∗ = 0.8 (unknown), (σ2)∗ = 0.1 (known)
 Effect of single data point
 Uninformative (vague/ flat) prior, σ2
0 →∞
1
2
0
2
2
02
0
2
2
0
2
0
2
2
1
1
1
1
−






+=
+
+
+
=
σσ
σµ
σσ
σ
σσ
σ
µ
N
N
x
N
N
N
~,
//
/
//
/
2
0
2
2
0
02
0
2
2
0
001
σσ
σ
µ
σσ
σ
µµµ
+
−−=
+
−+= )()( xxx
0µµ →N